Надежность восстанавливаемых объектов

Основные понятия

      Восстанавливаемым называется объект, для которого восстанов-ление работоспособного состояния предусмотрено в нормативно-технической документации. Для восстанавливаемых объектов характерно чередование работоспо-собного состояния и восстанов-ления работоспособности после отказа. Таким образом, процесс эксплуатации объекта можно представить как последова-тельное чередование интервалов времени работоспособного tpi и неработо-способного состояний t_вi (времени восстановления).

      В процессе эксплуатации восстанавливаемый объект может многокра-но отказывать. После каждого отказа происходит полное восстановление объекта, после чего он вновь применяется по назначению. Моменты отказов t₁, t₂, …, tm образуют поток отказов, а так как восстановления (например, заменой элементов) следуют мгновенно, то эти же моменты образуют поток восстановлений. Мгновенно – так как время вос-становления несравнимо мало по сравнению со временем работоспособного состояния. Отказы и восстановления можно рассматривать как поток событий: отказов или  восстановлений.

      В теории надежности для исследования восстанавливаемых объектов широко применяется простейший поток событий, который обладает следующими свойствами:

       - стационарностью – когда вероятность появления n отказов в проме-жутке времени зависит только от количества отказов n и длительности рассматриваемого интервала времени и не зависит от положения интервала времени на оси времени.

       - отсутствием последействия – когда вероятность наступления n отказов в течение интервала не зависит от того, сколько было отказов и как они распределялись до момента начала интервала времени;

       - ординарностью – когда появление в один и тот же момент времени более одного отказа невозможно.

       Показатели надежности восстанавливаемых объектов делятся на три группы: показатели безотказности, показатели ремонтопригодности;  комплексные показатели. При анализе надежности восстанавливаемых объектов до возникновения первого отказа к ним применяются те же критерии надежности, что и для невосстанавливаемых систем: - вероятность безотказной работы P(t), вероятность отказа Q(t),  частота отказов f(t), интенсивность отказов λ(t), средняя наработка до первого отказа Т (наработка до отказа). Но, как только в восстанавливаемой системе возникнет отказ, она восстанавливается до работоспособного состояния. После чего работает до возникновения следующего отказа. Эти циклы продолжаются до наступления предельного состояния или морального старения. Поэтому, в отличие от невосстанавливаемых объектов, рассматривают следующие параметры надежности: вероятность безотказной работы P(t), вероятность отказа Q(t); - параметр потока отказов ω(t), среднюю наработку на отказ Т (наработку на отказ).

       Статистически параметр потока отказов определяется как отношение числа отказавших элементов в единицу времени к числу элементов, постав-ленных на испытание при условии, что отказавшие образцы заменяются исправными. Размерность параметра потока отказов – ч^-1. Параметр потока отказов обладает следующим свойством:  если поток отказов и восстановлений стационарен, то ω (t) = ω = λ = const.  Для ординарных потоков отказов и восстановлений при известном па-раметре потока отказов можно определить возможное число отказовn(t) за время Δt.

Методы расчета надежности восстанавливаемых объектов

При расчете показателей надежности восстанавливаемых объектов и систем наиболее распространено допущение: экспоненциальное распределение наработки между отказами, экспоненциальное распределение времени восстановления. Применение экспоненциального распределения для описания процесса восстановления позволяет при ординарных независимых отказах представить анализируемые системы в виде марковских систем. При экспоненциальном распределении наработки между отказами и времени восстановления, для расчета надежности используют метод дифференциальных уравнений для вероятностей состояний (уравнений Колмогорова-Чепмена).

Случайный процесс в какой либо физической системе S, называется марковским, если он обладает следующим свойством: для любого момента t₀ вероятность состояния системы в будущем (t > t₀) зависит только от состояния в настоящем (t = t₀) и не зависит от того, когда и каким образом система пришла в это состояние (иначе: при фиксированном настоящем будущее не зависит от предыстории процесса - прошлого). Для марковского процесса «будущее» зависит от «прошлого» только через «настоящее», т. е. будущее протекание процесса зависит только от тех прошедших событий, которые повлияли на состояние процесса в настоящий момент. Марковский процесс, как процесс без последействия, не означает полной независимости от прошлого, поскольку оно проявляется в настоящем. При использовании метода, в общем случае, для системы S, необходимо иметь математическую модель в виде множества состояний системы S₁ , S₂ , … , S_n , в которых она может находиться при отказах и восстановлениях элементов.

Для рассмотрения принципа составления модели введены допущения:

- отказавшие элементы системы (или сам рассматриваемый объект) немедленно восстанавливаются (начало восстановления совпадает с моментом отказа);

- отсутствуют ограничения на число восстановлений;

- если все потоки событий, переводящих систему (объект) из состояния в состояние, являются пуассоновскими (простейшими), то случайный процесс переходов будет марковским процессом с непрерывным временем и дискретными состояниями S₁ , S₂ , … , S_n .

Основные правила составления модели:

1. Математическую модель изображают в виде графа состояний. Элементы графа:

а) кружки (вершины графа S₁ , S₂ , … , S_n ) – возможные состояния системы S, возникающие при отказах элементов;

б) стрелки – возможные направления переходов из одного состояния S_i в другое S_j .Над/под стрелками указываются интенсивности переходов.

Рис.9. Примеры графа

 

        На схеме оьозначены: S₀ – работоспособное состояние; S₁ – состояние отказа. «Петлей» обозначаются задержки в том или ином состоянии S₀ и S₁ соответствующие: исправное состояние продолжается; состояние отказа продолжается (в дальнейшем петли на графах не рассматриваем).

       Граф состояний отражает конечное (дискретное) число возможных состояний системы S₁ , S₂ , … , S_n . Каждая из вершин графа соответствует одному из состояний.

       2. Для описания случайного процесса перехода состояний (отказ/ восстановление) применяют вероятности состояний

 

P1(t), P2(t), … , P_i(t), … , Pn(t),

 

где P_i(t) – вероятность нахождения системы в момент t в i-м состоянии, т. е.

 

P_i(t) = P{S(t) = si}.

 

      Очевидно, что для любого t

 

(нормировочное условие, поскольку иных состояний, кроме S₁ , S₂ , … , S_n нет).

       3. По графу состояний составляется система обыкновенных дифференциальных уравнений первого порядка (уравнений Колмогорова-Чепмена

       При составлении дифференциальных уравнений пользуются простым мнемоническим правилом:

       а) в левой части – производная по времени t от P_i(t);

       б) число членов в правой части равно числу стрелок, соединяющих рассматриваемое состояние с другими состояниями;

       в) каждый член правой части равен произведению интенсивности перехода на вероятность того состояния, из которого выходит стрелка;

       г) знак произведения положителен, если стрелка входит (направлена острием) в рассматриваемое состояние, и отрицателен, если стрелка выходит из него.

       Проверкой правильности составления уравнений является равенство нулю суммы правых частей уравнений.

   4. Чтобы решить систему дифференциальных уравнений для вероятностей состояний P1(t), P_i(t), … , Pn(t) необходимо задать начальное значение вероятностей P1(0), P_i(0), … , Pn(0), при t = 0, сумма которых равна единице:

 

 

      Если в начальный момент t = 0 состояние системы известно, например, S(t=0) = Si, то P_i(0) = 1, а остальные равны нулю.

       2. Показатели надежности восстанавливаемых систем. Все состояния системы S можно разделить на подмножества:

SK S – подмножество состояний j = , в которых система работоспособна;

S_M S – подмножество состояний z = , в которых система неработоспособна.

S = S_K 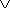S_M ,

S_K 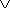S_M = 0.

       1. Функция готовности Г(t) системы определяет вероятность нахождения системы в работоспособном состоянии в момент t

где Pj(t) – вероятность нахождения системы в работоспособном j-м состоянии; Pz(t) – вероятность нахождения системы в неработоспособном z-м состоянии.

       2. Функция простоя П(t) системы

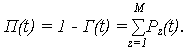
       3. Коэффициент готовности kг.с. системы определяется при установившемся режиме эксплуатации (при t ). При t устанавливается предельный стационарный режим, в ходе которого система переходит из состояния в состояние, но вероятности состояний уже не меняются

      Коэффициент готовности kг.с. можно рассчитать по системе (2) дифференциальных уравнений, приравнивая нулю их левые части dP_i(t)/dt = 0, т.к. P_i = const при t . Тогда система уравнений (2) превращается в систему алгебраических уравнений вида:

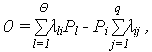
и коэффициент готовности:

есть предельное значение функции готовности при установившемся режиме t .4. Параметр потока отказов системы

где _jz – интенсивности (обобщенное обозначение) переходов из работоспособного состояния в неработоспособное.

      5. Функция потока отказов

      6. Средняя наработка между отказами на интервале t

---

Дата добавления: 2018-04-05; просмотров: 1978; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!