Последовательное соединение элементов в однофазной цепи синусоидального тока
Рассмотрим цепь переменного тока с последовательным соединением резистивного, индуктивного и емкостного элементов.

Рис. 3
Индуктивный и емкостной элементы обуславливают следующие сопротивления
 – индуктивное сопротивление,
– индуктивное сопротивление, 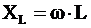 ,
,
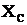 – емкостное сопротивление,
– емкостное сопротивление, 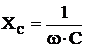 ,
,
где 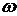 - угловая частота,
- угловая частота, 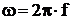 ,
,
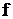 – циклическая частота,
– циклическая частота, 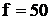 Гц.
Гц.
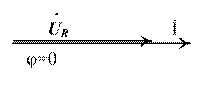
Между напряжениями на отдельных участках цепи существуют углы сдвига фаз, поэтому складывать их можно только векторно (рис.5).
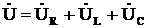 , (4)
, (4)
где 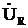 – активное падение напряжения.
Вектор – активное падение напряжения.
Вектор 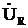 совпадает по фазе с вектором тока. Угол сдвига фаз совпадает по фазе с вектором тока. Угол сдвига фаз 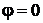 . .
| 
|
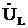 – индуктивное падение напряжения.
Вектор – индуктивное падение напряжения.
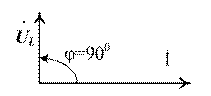
Вектор 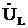 опережает вектор тока на опережает вектор тока на 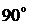 .
Угол сдвига фаз .
Угол сдвига фаз 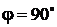 . .
| 
|
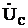 – емкостное падение напряжения.
Вектор – емкостное падение напряжения.
Вектор 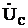 отстает от вектора тока на отстает от вектора тока на 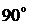 .
Угол сдвига фаз .
Угол сдвига фаз 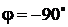 . .
| 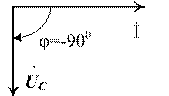 Рис. 4
Рис. 4
|
Модули этих напряжений равны:
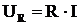 ,
, 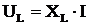 ,
, 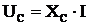 . (5)
. (5)
Для анализа и расчета электрических цепей применяются векторные диаграммы.
Векторная диаграмма – это совокупность векторов, изображающих синусоидальные токи, напряжения и ЭДС одинаковой частоты.
На векторных диаграммах длины векторов в масштабе равны действующим значениям этих величин. На топографической диаграмме необходимо учитывать последовательность соединения элементов, указанную на схеме, т.е. отразить топографию цепи. Первым проводят вектор той величины, которая общая для всех элементов цепи. Векторы остальных величин проводят под углами, равными их сдвигам фаз по отношению к первой основной величине. При этом опережающие векторы проводят против часовой стрелки, а отстающие – по часовой (рис.4).
|
|
|
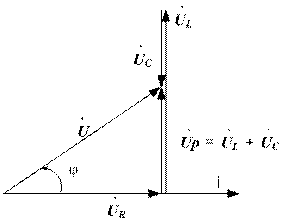 При сложении векторов их следует строить последовательно друг за другом, вектор суммы соединяет начало первого вектора с концом последнего и направляется в конец последнего.
При сложении векторов их следует строить последовательно друг за другом, вектор суммы соединяет начало первого вектора с концом последнего и направляется в конец последнего.
Построим векторную диаграмму последовательной цепи (рис. 3) по уравнению (4), считая, что 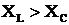 , а значит
, а значит 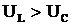 .
.
Первым проводится вектор тока 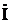 , общий для всех элементов последовательной цепи (рис. 5).
, общий для всех элементов последовательной цепи (рис. 5).
Векторы индуктивного и емкостного напряжения находятся в противофазе и длина вектора реактивного напряжения
Рис. 5 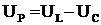 .
.
Из диаграммы следует, что модуль напряжения на входе цепи
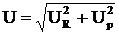 ,
,
где 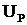 – модуль реактивного напряжения.
– модуль реактивного напряжения.
Подставив значения 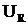 ,
, 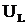 ,
, 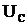 из формул (4), получим:
из формул (4), получим:
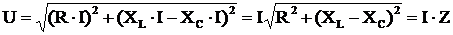 , (6)
, (6)
где 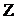 – полное сопротивление цепи переменного тока,
– полное сопротивление цепи переменного тока,
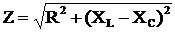 , (7)
, (7)
|
|
|
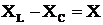 – реактивное сопротивление.
– реактивное сопротивление.
Из формулы (6) получим закон Ома для цепи переменного тока
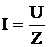 . (8)
. (8)
Индуктивное и емкостное сопротивления определяют не только значения токов в цепи, но также сдвиг фаз между напряжениями и токами, который можно найти из треугольника сопротивлений. На рис. 6. представлены треугольники сопротивлений: а) при 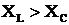 , б) при
, б) при 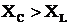 .
.
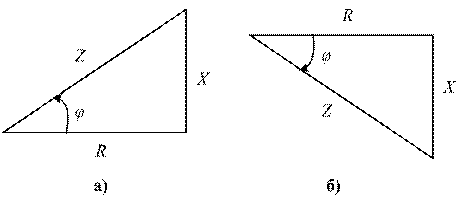
Рис. 6
 ,
, 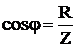 ,
, 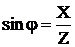 . (9)
. (9)
Энергетические процессы в цепи переменного тока характеризуются активной 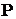 , реактивной
, реактивной  и полной
и полной 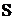 мощностями.
мощностями.
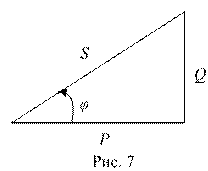
Они образуют прямоугольный треугольник мощностей см. рис. 7.
Активная мощность 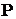 затрачивается на совершение работы в цепи и безвозвратно потребляется ею.
затрачивается на совершение работы в цепи и безвозвратно потребляется ею.
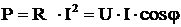 , Вт, кВт (10)
, Вт, кВт (10)
Реактивная мощность 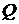 работы не совершает, а затрачивается на создание электрических и магнитных полей. Она обменивается между источником и цепью.
работы не совершает, а затрачивается на создание электрических и магнитных полей. Она обменивается между источником и цепью.
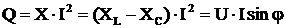 , вар, квар. (11)
, вар, квар. (11)
Полная мощность 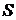 определяет наибольшее значение активной мощности, которое может быть получено при заданных значениях тока и напряжения, т.е. при
определяет наибольшее значение активной мощности, которое может быть получено при заданных значениях тока и напряжения, т.е. при 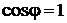 .
.
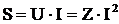 , ВА, кВА (12)
, ВА, кВА (12)
Из треугольника мощностей
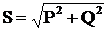 (13)
(13)
|
|
|
Отношение активной мощности к полной 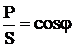 называется коэффициентом мощности. Он показывает, какую часть от полной мощности составляет активная мощность.
называется коэффициентом мощности. Он показывает, какую часть от полной мощности составляет активная мощность.
Пример 1. В цепи синусоидального тока (рис. 8) последовательно включены: резистор с сопротивлением 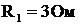 , индуктивное сопротивление
, индуктивное сопротивление 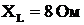 , резистор с сопротивлением
, резистор с сопротивлением 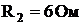 , емкостное сопротивление
, емкостное сопротивление 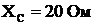 . Входное напряжение
. Входное напряжение 
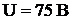 .
.
Определить:
1) полное сопротивление цепи 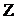 ; 2) ток
; 2) ток 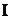 ; 3) угол сдвига фаз
; 3) угол сдвига фаз 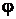 между входным напряжением и током (по величине и по знаку); 4) активную
между входным напряжением и током (по величине и по знаку); 4) активную 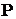 , реактивную
, реактивную  и полную
и полную 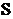 мощности цепи.
мощности цепи.
Начертить в масштабе векторную диаграмму цепи, пояснить порядок ее построения.
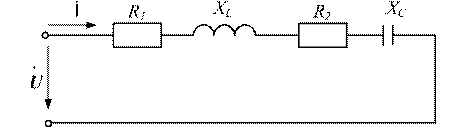
Рис. 8
Решение:
1) Полное сопротивление цепи (7)
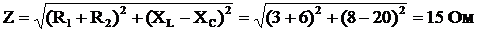 ;
;
2) Ток в цепи по закону Ома (8) 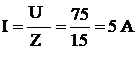 ;
;
3) Угол сдвига фаз (9) 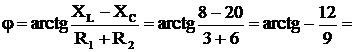
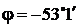 ;
;
4) Активная мощность (10) 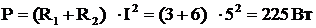 ,
,
Реактивная мощность (11)  , знак «-» указывает на то, что цепь носит емкостной характер.
, знак «-» указывает на то, что цепь носит емкостной характер.
Полная мощность по (12) 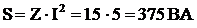 , или по (13)
, или по (13)
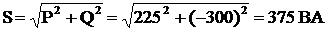 ;
;
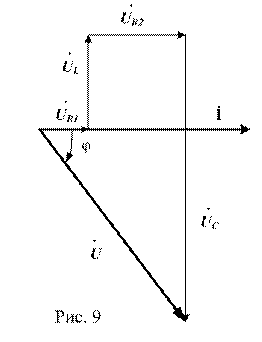
5) Построение векторной диаграммы (рис. 9) по уравнению (4)
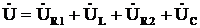 .
.
Модули напряжений (5) 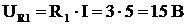 ,
, 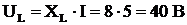 ,
, 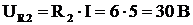 ,
, 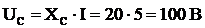 .
.
 Принимаем масштаб по напряжению
Принимаем масштаб по напряжению 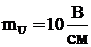 .
.
Первым откладываем вектор тока 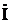 , принимая его начальную фазу равной нулю. Зная модули и направления векторов напряжений
, принимая его начальную фазу равной нулю. Зная модули и направления векторов напряжений 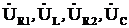 , определяем модуль и направление вектора входного напряжения
, определяем модуль и направление вектора входного напряжения 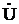 , соединив начало вектора
, соединив начало вектора 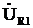 с концом вектора
с концом вектора 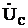 .
.
|
|
|
При этом учитываем, что векторы активных напряжений 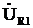 и
и 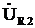 совпадают по фазе с током, вектор индуктивного напряжения
совпадают по фазе с током, вектор индуктивного напряжения 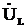 опережает вектор тока на
опережает вектор тока на 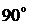 , а вектор емкостного напряжения
, а вектор емкостного напряжения 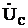 отстает от вектора тока на
отстает от вектора тока на 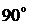 .
.
Дата добавления: 2018-04-05; просмотров: 172; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
