НОРМАЛЬНЫЕ ФОРМЫ БУЛЕВЫХ ФУНКЦИЙ
Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный университет
Имени Франциска Скорины»
В.Н. СЕМЕНЧУК
ДИСКРЕТНАЯ МАТЕМАТИКА
ПРАКТИЧЕСКОЕ ПОСОБИЕ
Гомель 2007
Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный университет
Имени Франциска Скорины»
В.Н. СЕМЕНЧУК
ДИСКРЕТНАЯ МАТЕМАТИКА
ПРАКТИЧЕСКОЕ ПОСОБИЕ
ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ
для студентов 1 курса
специальности 1–31 03 03 – «Прикладная математика»
Гомель 2007
УДК 519.14(075.8)
ББК 22.174 я73
С 305
Рецензенты:
А.Н.Скиба,профессор, доктор физико-математических наук;
кафедра высшей математики учреждения образования
«Гомельский государственный университет имени
Франциска Скорины»
Рекомендовано к изданию научно-методическим
советом учреждения образования «Гомельский
государственный университет имени Франциска Скорины»
| С 305 | Семенчук, В.Н. Дискретная математика [Текст]: практ. пособ. для студентов специальности 1-31 03 03 «Прикладная математика» / В.Н. Семенчук; М-во образов. РБ, Гомельский государственный университет им. Ф. Скорины.– Гомель: УО «ГГУ им. Ф. Скорины», 2007.– с. |
ISBN
Практическое пособие ставит своей целью оказание помощи студентам в усвоении основных методов дискретной математики и их применения при решении практических задач. Данное пособие может быть использовано для самостоятельной работы студентов и предназначено для студентов математического факультета специальности «Прикладная математика».
|
|
|
УДК 519.14(075.8)
ББК 22.174 я73
ISBN © В.Н. Семенчук, 2007
© УО «ГГУ им. Ф.Скорины», 2007
СОДЕРЖАНИЕ
| Введение …………………………………………………………….. | 4 |
| Тема 1 Булевы функции………………………..………………… | |
| Тема 2 Нормальные формы булевых функций ………………… | |
| Тема 3 Минимизация булевых функций……………………..…. | |
| Тема 4 Контактные и логические схемы………………………... | |
| Тема 5 Полнота и замкнутость ……………………..…………… | |
| Тема 6 Алгебра логики предикатов …………………………....... | |
| Тема 7 Конечные автоматы……………………………………… | |
| Тема 8 Рекуррентные функции ………………………………….. | |
| Тема 9 Машины Тьюринга……………………………………….. |
ВВЕДЕНИЕ
Настоящее учебное пособие посвящено изучению таких важных разделов дискретной математики, как теория булевых функций, теория графов, теория кодирования, теория алгоритмов, теория конечных автоматов. В него включены девять лабораторных работ: булевы функции, нормальные формы булевых функций, минимизация булевых функций, контактные и логические схемы, полнота и замкнутость, алгебра логики предикатов, конечные автоматы, рекурсивные функции и машина Тьюринга.
|
|
|
Данное пособие может рассматриваться студентами как «специальный курс на дому». Перед каждой лабораторной работой приводится необходимый теоретический материал, затем следует решение и разбор типовых задач, приводятся вопросы для самостоятельного контроля и список рекомендованной литературы.
Тема 1
БУЛЕВЫ ФУНКЦИИ
1.1 Высказывания.
1.2 Операции над высказываниями.
1.3 Понятие булевой функции, элементарные булевы функции.
Основные понятия по теме
Функцией алгебры логики (булевой функцией)  от переменных
от переменных  называется функция, принимающая значения 1,0 и аргументы которой также принимают значения 1,0.
называется функция, принимающая значения 1,0 и аргументы которой также принимают значения 1,0.
Всякая булева функция от 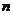 переменных может быть задана с помощью таблицы истинности
переменных может быть задана с помощью таблицы истинности

| 
| 
| 
| 
| 
|
0
0
0
 1
1
| 0
0
0
 1
1
| 




| 0
0
1
 1
1
| 0
1
0
 1
1
| 

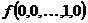

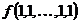
|
|
|
|
Данная таблица состоит из  строк, причем в ней все наборы (
строк, причем в ней все наборы (  ) расположены в порядке возрастания их номеров. Следующие булевы функции мы будем называть элементарными.
) расположены в порядке возрастания их номеров. Следующие булевы функции мы будем называть элементарными.
 - константа 0;
- константа 0;
 - константа 1;
- константа 1;
 - тождественная функция;
- тождественная функция;
 - отрицание
- отрицание 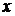 ;
;
 - конъюнкция
- конъюнкция 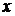 и
и 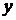 ;
;
 - дизъюнкция
- дизъюнкция 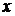 и
и 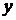 ;
;
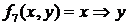 - импликация
- импликация 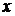 и
и 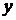 ;
;
 - эквивалентность
- эквивалентность 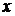 и
и 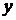 ;
;
 - сложение
- сложение 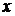 и
и 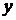 по
по  2;
2;
 - функция Шеффера;
- функция Шеффера;
 - функция Пирса.
- функция Пирса.
Данные функции задаются следующими таблицами истинности
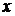
| 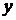
| 
| 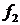
| 
| 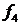
| 
| 
| 
| 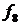
| 
| 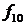
| 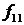
|
| 0 0 1 1 | 0 1 0 1 | 0 0 0 0 | 1 1 1 1 | 0 0 1 1 | 1 1 0 0 | 0 0 0 1 | 0 1 1 1 | 1 1 0 1 | 1 0 0 1 | 0 1 1 0 | 1 1 1 0 | 1 0 0 0 |
Приведем определение формулы алгебры логики:
1. каждая элементарная булева функция – формула;
2. если некоторое выражение 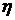 есть формула, то
есть формула, то 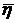 тоже формула;
тоже формула;
3. если некоторые выражения  и
и 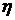 есть формулы, то выражения
есть формулы, то выражения 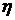

 ,
, 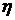
 ,
, 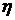

 ,
, 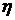

 ,
, 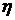 +
+  ,
, 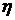

 ,
, 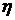

 тоже формулы;
тоже формулы;
4. других формул: кроме построенных в п. 1–3 нет.
С целью упрощения записи формул, договоримся, что операция конъюнкция «сильнее» других логических операций, т.е. если в формуле нет скобок, то вначале выполняется операция конъюнкция.
|
|
|
Две формулы 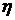 и
и  называются равносильными, если они определяют одну и ту же булеву функцию (запись
называются равносильными, если они определяют одну и ту же булеву функцию (запись 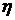 =
=  будет означать, что фор-
будет означать, что фор-
мулы 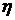 и
и  равносильны).
равносильны).
Приведем перечень важнейших равносильностей (законов) алгебры логики.
1.  – закон тождества;
– закон тождества;
2.  – закон противоречия;
– закон противоречия;
3. 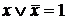 – закон исключения третьего;
– закон исключения третьего;
4.  – закон двойного отрицания;
– закон двойного отрицания;
5.  ,
,  – законы идемпотентности;
– законы идемпотентности;
6.  ,
,  – законы коммутативности;
– законы коммутативности;
7. 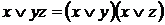 ,
,  – законы дистрибутивности;
– законы дистрибутивности;
8. 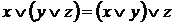 ,
,  – законы ассоциативности;
– законы ассоциативности;
9.  ,
, 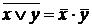 – законы де Моргана;
– законы де Моргана;
10.  ,
, 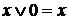 ,
, 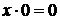 ,
,  .
.
11.  ,
,  –законы поглощения;
–законы поглощения;
12.  ,
,  –законы склеивания.
–законы склеивания.
Отметим следующие важнейшие равносильности
1. 
2. 
3. 
4. 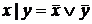
5. 
6. 
7. 
Формула алгебры логики называется тавтологией (тождественно истинной), если при любых значениях переменных она принимает истинное значение.
Формула алгебры логики называется противоречием (тождественно ложной), если при любых значениях переменных она принимает ложное значение.
Формула алгебры логики называется выполнимой, если найдется такой набор значений переменных, при котором ее значение истинно.
Пример 1 Является ли формула  тавтологией?
тавтологией?
1 способ (табличный)
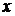
| 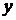
| 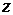
| 
| 
| 
| 
| 
| 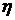
|
| 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 | 1 0 0 1 1 0 0 1 | 1 1 1 1 1 0 0 1 | 1 1 1 1 0 0 1 1 | 1 1 1 1 0 1 0 1 | 1 1 1 1 1 0 0 1 | 1 1 1 1 1 1 1 1 |
2 способ (аналитический)


Пример 2 Является ли формула  тавтологией?
тавтологией?
Метод от противного.
Пусть  .
.
Тогда  . Отсюда
. Отсюда 
Из последнего следует, что  . Тогда
. Тогда  ,
, 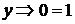 , что невозможно.
, что невозможно.
Пример 3 Равносильны ли формулы?
 ;
; 





Следовательно, формулы равносильны.
Пример 4 Упростить 
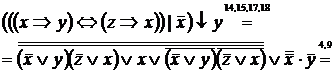

Пример 5 Решить уравнение 
Это уравнение равносильно следующей системе

Из второго уравнения следует, что  ,
,  . Ясно, что тогда
. Ясно, что тогда  . Подставляя в третье уравнение
. Подставляя в третье уравнение  . Следовательно,
. Следовательно, 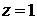 . Итак,
. Итак,  ,
,  ,
, 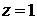 - решение искомого уравнения.
- решение искомого уравнения.
Лабораторная работа №1
I. Построить таблицы истинности для формул
1) 
2) 
3) 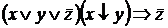
4) 
5) 
6) 
7) 
8) 
9) 
10) 
II. Без построения таблиц истинности докажите, что следующие формулы являются тавтологиями
1) 
2) 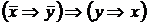
3) 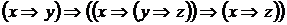
4) 
5) 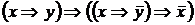
6) 
7) 
8) 
9) 
10) 
III. Без построения таблиц истинности докажите, что следующие формулы являются противоречием
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 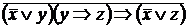
9) 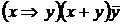
10) 
IV. Решить уравнения
1) 
2) 
3) 
4) 
5) 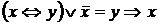
6) 
7) 
8) 
9) 
10) 
V. Какие из приведенных ниже формул являются тавтологиями, противоречиями, выполнимыми
1) 
2) 
3) 
4) 
5) 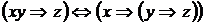
6) 
7) 
8) 
9) 
10) 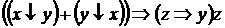
VI. Упростить
1) 
2) 
3) 
4) 
5) 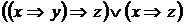
6) 
7) 
8) 
9) 
10) 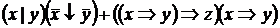
VII. Равносильны ли следующие формулы
1) 

2) 
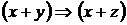
3) 

4) 
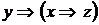
5) 

6) 

7) 

8) 
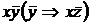
9) 

10) 

Вопросы для самоконтроля
1 Булевы функции. Таблицы истинности.
2 Число булевых функций от 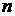 переменных.
переменных.
3 Элементарные булевы функции.
4 Формулы алгебры логики. Классификация формул.
5 Равносильные формулы. Законы равносильности.
6 Логические уравнения.
Литература
1 Карпов, В.Г. Математическая логика и дискретная математика [Текст] : учебное пособие для студентов университетов/ В.Г.Карпов, В.А.Мощенский. – Мн.: Вышэйшая школа, 1977. – 255с.
2 Яблонский, С.В. Введение в дискретную математику [Текст] : учебное пособие для вузов по специальности «Прикладная математика»/ С.В.Яблонский. – М.: Наука, 1979. – 272с.
3 Мощенский, В.А. Лекции по математической логике [Текст] : учебное пособие для студентов математических специальностей вузов/ В.А.Мощенский. – Мн.: Изд. центр БГУ, 1973. – 159с.
Тема 2
НОРМАЛЬНЫЕ ФОРМЫ БУЛЕВЫХ ФУНКЦИЙ
2.1 Дизъюнктивная нормальная форма (ДНФ).
2.2 Конъюнктивная нормальная форма (КНФ).
2.3 Совершенные дизъюнктивная и конъюнктивная нормальные формы и алгоритмы их построения.
Основные понятия по теме
Введем обозначение

Формула  , где
, где  ,
, 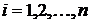 , а среди переменных
, а среди переменных 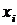 могут быть совпадающие, называется элементарной конъюнкцией.
могут быть совпадающие, называется элементарной конъюнкцией.
Дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой (сокращенно ДНФ).
Элементарная конъюнкция называется правильной, если в нее каждая переменная входит не более одного раза (включая ее вхождение под знаком отрицания).
Правильная элементарная конъюнкция называется полной относительно переменных  , если в нее каждая из этих переменных входит один и только один раз.
, если в нее каждая из этих переменных входит один и только один раз.
Совершенной дизъюнктивной нормальной формой (СДНФ) относительно переменных  называется дизъюнктивная нормальная форма, в которой нет одинаковых элементарных конъюнкций и все элементарные конъюнкции правильны и полны относительно переменных
называется дизъюнктивная нормальная форма, в которой нет одинаковых элементарных конъюнкций и все элементарные конъюнкции правильны и полны относительно переменных  .
.
Всякую булеву функцию  , не равную тождественно нулю, можно представить совершенной дизъюнктивной нормальной формой:
, не равную тождественно нулю, можно представить совершенной дизъюнктивной нормальной формой:
 (1)
(1)
Пример 1 Найти ДНФ для формулы 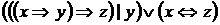 .
.
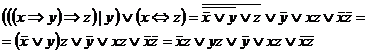
Пример 2 Найти СДНФ для формулы 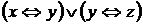 .
.
1 способ (табличный). Данный способ основан на разложении (1). Суть его состоит в следующем:
1. составляется таблица истинности для данной формулы;
2. в таблице истинности выделяются наборы  , для которых значение формулы истинно;
, для которых значение формулы истинно;
3. для каждого такого набора составляются элементарные конъюнкции;
4. составляем дизъюнкции построенных элементарных конъюнкций.
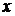
| 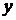
| 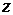
| 
| 
| 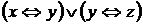
|
| 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 | 1 1 0 0 0 0 1 1 | 1 0 0 1 1 0 0 1 | 1 1 0 1 1 0 1 1 |


2 способ (аналитический).

 .
.
Формула вида  называется элементарной дизъюнкцией.
называется элементарной дизъюнкцией.
Всякая конъюнкция элементарных дизъюнкций называется конъюнктивной нормальной формой (КНФ).
Элементарная дизъюнкция называется правильной, если у нее каждая переменная входит не более одного раза (включая ее вхождение под знаком отрицания).
Правильная элементарная конъюнкция называется полной относительно переменных  , если каждая из этих переменных входит в нее один и только один раз (быть может, под знаком отрицания).
, если каждая из этих переменных входит в нее один и только один раз (быть может, под знаком отрицания).
Совершенной конъюнктивной нормальной формой (СКНФ) относительно переменных  называется конъюнктивная нормальная форма, в которой нет одинаковых элементарных дизъюнкций и все элементарные дизъюнкции правильны и полны относительно переменных
называется конъюнктивная нормальная форма, в которой нет одинаковых элементарных дизъюнкций и все элементарные дизъюнкции правильны и полны относительно переменных  .
.
Всякую функцию  отличную от тождественно истинной, можно представить совершенной конъюнктивной нормальной формой:
отличную от тождественно истинной, можно представить совершенной конъюнктивной нормальной формой:
 (2)
(2)
где символ  означает, что конъюнкция берется по тем наборам, которые указаны под ним.
означает, что конъюнкция берется по тем наборам, которые указаны под ним.
Пример 3 Найти КНФ для формулы  .
.

 .
.
Пример 4 Найти СКНФ для формулы  .
.
1 способ (табличный). Данный способ основан на разложении (2). Суть его состоит в следующем:
1. составляется таблица истинности для данной формулы;
2. в таблице истинности выделяются наборы  , для которых значение формулы ложно;
, для которых значение формулы ложно;
3. для каждого такого набора составляются элементарная дизъюнкция  ;
;
4. составляем конъюнкцию элементарных дизъюнкций.
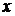
| 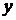
| 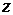
| 
| 
| 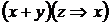
|
| 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 | 0 0 1 1 1 1 0 0 | 1 0 1 0 1 1 1 1 | 0 0 1 0 1 1 0 0 |

 .
.
2 способ (аналитический).



 .
.
Полиномом Жегалкина называется полином вида

причем в каждом наборе  все различны, а суммирование ведется по некоторому множеству таких не совпадающих наборов,
все различны, а суммирование ведется по некоторому множеству таких не совпадающих наборов,  - константа 0 или 1.
- константа 0 или 1.
Справедливы следующие равносильности:
1. 
2. 
3. 
4. 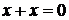
5. 
Каждая булева функция может быть единственным образом выражена при помощи полинома Жегалкина.
Пример 5 Выразить формулу  в виде полинома Жегалкина.
в виде полинома Жегалкина.
1 способ (метод неопределенных коэффициентов).
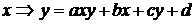
При  имеем:
имеем:  ;
;
При  имеем:
имеем:  ;
;
При  имеем:
имеем:  ;
;
При  имеем:
имеем:  , т.е.
, т.е.  .
.
Отсюда  .
.
2 способ.

Приведем полиномы Жегалкина элементарных булевых функций





Лабораторная работа №2
I. Найти ДНФ для формулы
1) 
2) 
3) 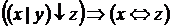
4) 
5) 
6) 
7) 
8) 
9) 
10) 
II. Найти СДНФ для формулы
1) 
2) 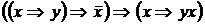
3) 
4) 
5) 
6) 
7) 
8) 
9) 
10) 
III. Найти КНФ для формулы
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
9) 
10) 
IV. Найти СКНФ для формулы
1) 
2) 
3) 
4) 
5) 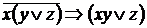
6) 
7) 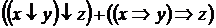
8) 
9) 
10) 
V. Найти полином Жегалкина для формулы
1) 
2) 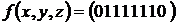
3) 
4) 
5) 
6) 
7) 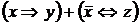
8) 
9) 
10) 
Вопросы для самоконтроля
1 Разложение булевых функций по переменным.
2 ДНФ и КНФ. Алгоритм их нахождения.
3 СДНФ и СКНФ. Алгоритмы их нахождения.
4 Полином Жегалкина, алгоритмы его нахождения.
Литература
1 Карпов, В.Г. Математическая логика и дискретная математика [Текст] : учебное пособие для студентов университетов/ В.Г.Карпов, В.А.Мощенский. – Мн.: Вышэйшая школа, 1977. – 255с.
2 Яблонский, С.В. Введение в дискретную математику [Текст] : учебное пособие для вузов по специальности «Прикладная математика»/ С.В.Яблонский. – М.: Наука, 1979. – 272с.
3 Мощенский, В.А. Лекции по математической логике [Текст] : учебное пособие для студентов математических специальностей вузов/ В.А.Мощенский. – Мн.: Изд. Центр БГУ, 1973. – 159с.
Тема 3
МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ
3.1 Сокращенная ДНФ.
3.2 Алгоритмы построения сокращенной ДНФ.
3.3 Алгоритм построения тупиковой ДНФ.
3.4 Импликантная матрица.
Основные понятия по теме
Дизъюнктивная нормальная форма называется минимальной, если она включает минимальное число символов по сравнению со всеми другими эквивалентными ей дизъюнктивными нормальными формами.
Заметим, что если некоторый символ в формуле, скажем, 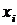 встречается, например, два раза, то при подсчете числа символов в формуле он учитывается два раза.
встречается, например, два раза, то при подсчете числа символов в формуле он учитывается два раза.
Рангом правильной элементарной конъюнкции называется число символов, входящих в нее.
Сопоставим каждой булевой функции  подмножество
подмножество  , которое будем называть областью истинности функции
, которое будем называть областью истинности функции  .
.
Пусть  - ДНФ, где
- ДНФ, где  - элементарные конъюнкции. Подмножество
- элементарные конъюнкции. Подмножество  называется интервалом
называется интервалом  -го ранга, если оно соответствует элементарной конъюнкции
-го ранга, если оно соответствует элементарной конъюнкции 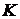
 -го ранга. С каждой ДНФ функции
-го ранга. С каждой ДНФ функции  связано покрытие
связано покрытие  интервалами
интервалами  , таких что
, таких что 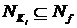 .
.
Интервал 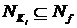 , называется максимальным для булевой функции, если не существует интервала
, называется максимальным для булевой функции, если не существует интервала  такого, что
такого, что  .
.
Если  - список всех максимальных интервалов подмножества
- список всех максимальных интервалов подмножества  , то
, то  .
.
ДНФ 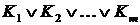 булевой функции
булевой функции  , соответствующая покрытию подмножества
, соответствующая покрытию подмножества  всеми максимальны ми интервалами, называется сокращенной ДНФ функции
всеми максимальны ми интервалами, называется сокращенной ДНФ функции  .
.
Сокращенная ДНФ для любой булевой функции  определяется однозначно.
определяется однозначно.
Рассмотрим алгоритмы построения сокращенная ДНФ.
1 алгоритм – табличный.
Пример 1 Найти сокращенную ДНФ для  .
.

Найдем 
Интервалы  и
и  - все максимальные интервалы
- все максимальные интервалы  - сокращенная ДНФ.
- сокращенная ДНФ.
2 алгоритм – метод Блейка:
1) находим ДНФ;
2) производим обобщенные склеивания  до тех пор, пока это возможно;
до тех пор, пока это возможно;
3) применяем правило поглощения  .
.
Пример 2 Найти сокращенную ДНФ для 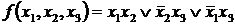 .
.
Применяя правило обобщенного склеивания, получаем:

Затем правило поглощения и находим сокращенную ДНФ  .
.
3 алгоритм – метод Нельсона:
1) находим КНФ;
2) разрываем скобки в соответствии с дистрибутивным законом;
3) применяем правило поглощения.
Пример 3 Найти сокращенную ДНФ для функции  .
.
После раскрытия скобок с помощью дистрибутивного закона, получаем  . Так как
. Так как  ,
,  , то имеем
, то имеем  .
.
Применяя правило поглощения, получаем сокращенную ДНФ.
IV алгоритм – метод минимизирующих карт.
Пример 4 Найти сокращенную ДНФ для функции  .
.
Составим минимизирующую карту для данной функции.

| 0 | 0 | 1 | 1 | |

| 

| 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 |
Объединяя соседние клетки, соответствующие единичным значениям булевой функции  в максимальные интервалы, и сопоставляя им элементарные конъюнкции, получим сокращенную ДНФ. Отметим, что клетки, расположенные по краям таблицы, также считаются соседними.
в максимальные интервалы, и сопоставляя им элементарные конъюнкции, получим сокращенную ДНФ. Отметим, что клетки, расположенные по краям таблицы, также считаются соседними.
Выпишем все максимальные интервалы










Итак,  - требуемая сокращенная ДНФ.
- требуемая сокращенная ДНФ.
Следующее утверждение устанавливает связь между минимальной и сокращенной ДНФ.
Минимальная ДНФ булевой функции получается из сокращенной ДНФ данной функции путем удаления некоторых элементарных конъюнкций.
Покрытие множества 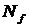 максимальными интервалами называется неприводимым, если после удаления из него любого интервала оно перестает быть покрытием. ДНФ булевой функции, соответствующее неприводимому покрытию, называется тупиковой.
максимальными интервалами называется неприводимым, если после удаления из него любого интервала оно перестает быть покрытием. ДНФ булевой функции, соответствующее неприводимому покрытию, называется тупиковой.
Всякая минимальная ДНФ является тупиковой.
Общая схема решения задачи минимизации булевых функций состоит в следующем:
1. выделяются все максимальные интервалы и строится сокращенная ДНФ;
2. строятся все тупиковые ДНФ;
3. среди всех тупиковых ДНФ выделяются все минимальные ДНФ.
Рассмотрим алгоритм построения всех тупиковых ДНФ. Суть данного алгоритма состоит в следующем:
1. для булевой функции  строим сокращенную ДНФ;
строим сокращенную ДНФ;
2. для каждого набора  из
из  ,
,  выделяем в сокращенной ДНФ функции
выделяем в сокращенной ДНФ функции  все такие элементарные конъюнкции
все такие элементарные конъюнкции  , что
, что  ,
,  ;
;
3. составляем выражение вида
 (*)
(*)
4. применяем к выражению вида (*) законы дистрибутивности и поглощения. В результате получаем

Теперь каждая ДНФ  является тупиковой ДНФ функции
является тупиковой ДНФ функции  .
.
Рассмотрим работу данного алгоритма на следующем примере.
Пример 5 Найти все тупиковые ДНФ для булевой функции  .
.
Найдем сокращенную ДНФ данной функции по методу Нельсона. Для этого составим СКНФ данной функции, используя разложение (2)

Применяя закон дистрибутивности, получаем: 
Обозначим  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
 составляем выражение (*)
составляем выражение (*)





Таким образом,  имеет шесть тупиковых ДНФ
имеет шесть тупиковых ДНФ






Две из них  и
и  являются минимальными ДНФ (метод Квайна).
являются минимальными ДНФ (метод Квайна).
Рассмотрим метод импликантных матриц нахождения минимальных ДНФ.
Для булевой функции  находим сокращенную ДНФ
находим сокращенную ДНФ  . Построим для этой функции импликантную матрицу, представляющую собой таблицу, в вертикальные входы которой записываются
. Построим для этой функции импликантную матрицу, представляющую собой таблицу, в вертикальные входы которой записываются  , и в горизонтальные
, и в горизонтальные 

| 
| 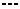
| 
| 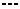
| 
| |

| ||||||

| ||||||
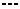
| ||||||

| + | |||||
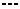
| ||||||

|
Для каждой  находим набор
находим набор  такой, что
такой, что  . Клетку импликантной матрицы, образованную пересечением
. Клетку импликантной матрицы, образованную пересечением  -ой строки и
-ой строки и  -ого столбца отметим крестиком.
-ого столбца отметим крестиком.
Чтобы получить минимальную ДНФ заданной функции, достаточно найти минимальное число  ,
,  , которые совместно накрывают крестиками все столбцы импликантной матрицы.
, которые совместно накрывают крестиками все столбцы импликантной матрицы.
Пример 6 Найти минимальные ДНФ для функции 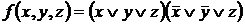 .
.
Из предыдущего примера следует, что сокращенная ДНФ для данной функции  .
.
Строим импликантную матрицу

| 
| 
| 
| 
| 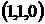
| |
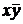
| + | + | ||||

| + | + | ||||
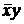
| + | + | ||||

| + | + | ||||

| + | + | ||||

| + | + |
Из таблицы видно, что данная функция имеет две минимальные ДНФ: 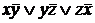 ,
,  .
.
Лабораторная работа №3
I. Найти сокращенную ДНФ графическим методом
1) 
2) 
3) 
4) 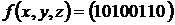
5) 
6) 
7) 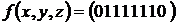
8) 
9) 
10) 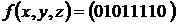
II. Найти сокращенную ДНФ методом Блейка
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
9) 
10) 
III. Найти сокращенную ДНФ методом Нельсона
1) 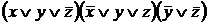
2) 
3) 
4) 
5) 
6) 
7) 
8) 
9) 
10) 
IV. Найти сокращенную ДНФ методом минимизирующих карт
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
9) 
10) 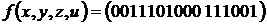
VI. Найти все минимальные ДНФ
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
9) 
10) 
Вопросы для самоконтроля
1 Минимальная дизъюнктивная нормальная форма.
2 Область истинности булевой функции.
3 Интервал.
4 Покрытие области истинности.
5 Сокращенная ДНФ.
6 Алгоритмы построения сокращенной ДНФ (Блейка, Нельсона, минимизирующих карт).
7 Неприводимое покрытие.
8 Тупиковые ДНФ и алгоритм их построения.
9 Метод импликантных матриц (метод Квайна).
Литература
1 Карпов, В.Г. Математическая логика и дискретная математика [Текст]: учебное пособие для студентов университетов/ В.Г.Карпов, В.А.Мощенский. – Мн.: Вышэйшая школа, 1977. – 255с.
2 Яблонский, С.В. Введение в дискретную математику [Текст]: учебное пособие для вузов по специальности «Прикладная математика»/ С.В.Яблонский. – М.: Наука, 1979. – 272с.
Тема 4
Дата добавления: 2018-04-04; просмотров: 3486; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
