Лабораторная работа № 1. Последовательное соединение звеньев

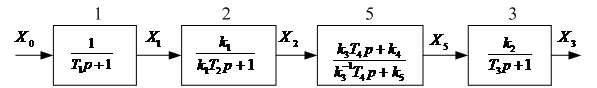
      Таблица 1

Вариант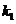
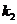
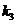
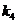
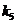
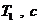
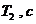
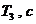
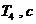
1-1 1-2 1-3	1 1 1	1 1 1	0.5 4 4	1 1 0	1 1 1	0.156 0.156 0.156	0.1 0.1 0.1	0.176 0.176 0.176	0.2 0.2 0.2
2-1 2-2 2-3	1 1 1	1 1 1	0.5 4 4	1 1 0	1 1 1	0.208 0.208 0.208	0.1 0.1 0.1	0.264 0.264 0.264	0.2 0.2 0.2
3-1 3-2 3-3	1 1 1	1 1 1	0.5 4 4	1 1 0	1 1 1	0.412 0.412 0.412	0.2 0.2 0.2	0.088 0.088 0.088	0.44 0.44 0.44
4-1 4-2 4-3	1 1 1	1 1 1	0.5 2 2	1 1 0	1 1 1	0.208 0.208 0.208	0.1 0.1 0.1	0.176 0.176 0.176	0.44 0.44 0.44

Программа самостоятельной работы

1. По заданным параметрам своего варианта (табл. 1) рассчитать и построить аппроксимированные и точные логарифмические амплитудные (ЛАЧХ) и фазовые (ЛФЧХ) частотные характеристики каскадов звеньев:
1; 1-2; 1-2-5-3.

2. По заданным вариантам остальных двух членов бригады построить аппроксимированные ЛАЧХ каскада 1-2-5-3.

3. Построить приближенные переходные функции и определить основные показатели переходного процесса при ступенчатом входном воздействии в указанных каскадах звеньев (1; 1-2; 1-2-5-3) для своего варианта и в каскаде 1-2-5-3 для остальных вариантов своей бригады.

4. Результаты расчёта свести в таблицы и графики.

Программа работ в лаборатории

1. Собрать исследуемую систему в рабочем поле компьютера в соответствии с заданной структурной схемой (рис. 1).

2. С помощью компьютера снять кривые переходных процессов на выходах 1,2 и 3 звеньев системы при подаче на вход звена 1 единичного ступенчатого воздействия.

3. Определить основные показатели переходных процессов (установившееся 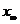и максимальное 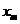отклонения, перерегулирование s, время переходного процесса 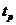), занести в таблицы и сопоставить их с расчётными значениями.

Методические указания к работе № 1

При последовательном соединении n звеньев с передаточными функциями 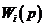, АЧХ, ЛАЧХ и ЛФЧХ – соответственно 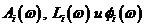, результирующие 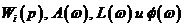равны

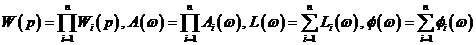. (1.1)

В исследуемой САУ звенья 1, 2, 3 являются апериодическими (или инерционными). Апериодическое звено описывается во времени дифференциальным неоднородным уравнением 1-го порядка

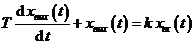.          (1.2)

Его передаточная функция и частотные характеристики имеют вид

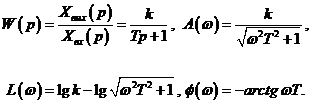                  (1.3)

При k =1, 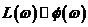зависят лишь от значений 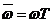, что позволяет строить их однообразно. Значения  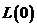  (ЛАЧХ при w=0, т. е. lgw=-¥) равны lg k, например, при k=1 равны нулю, при k >1 лежат выше оси абсцисс, а при k <1 – ниже оси абсцисс. Данные расчета ЛАЧХ при k= 1 и ЛФЧХ по формулам (1.3) приведены в таблице (рис. 2), причем если построение вести в масштабах, рекомендованных в п. 1.2.3, то шаг по оси абсцисс lgw равен 1 см. Значения lg 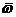=lgwТ равны нулю при собственной частоте  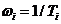(частоте сопряжения участков аппроксимированной ЛАЧХ), отрицательны – при 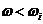и положительны – при .

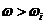На рис. 2 приведены уточнённые ЛАЧХ( 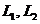) и ЛФЧХ ( 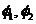) звеньев 1 и 2 при Т₁=0,1с ( 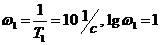), k₁=2, Т₂=0,25 с, k₁·Т₂=0,5 с,  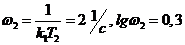( ), рассчитанные по формулам (1.1). Там же приведены ЛАЧХ, аппроксимированные отрезками прямых линий.

Для ускорения процесса построения ЛЧХ апериодических звеньев рекомендуется вырезать из картона шаблоны L и j (заштриховано на рис.2). При этом уточнённые ЛЧХ апериодического звена строятся в следующем порядке:

1) находится частота сопряжения ;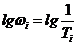

2) вычерчивается аппроксимированная ЛАЧХ в виде отрезка прямой с нулевым наклоном, проведенной по координате lgk до частоты сопряжения 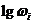, и отрезка с наклоном – 1 лог на декаду ( на рис. 2) и частотах больших lg ;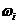

3) накладывается шаблон, как указано на рис. 2, и вычерчиваются уточненные ЛАЧХ и ЛФЧХ.

 Переходная функция апериодического звена, т. е. изменение 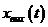 при ступенчатом единичном воздействии на входе , может быть найдена решением уравнения (1.2):

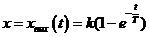.                     (1.4)

На рис. 2 представлена таблица 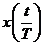, рассчитанная по формуле (1.4), и кривые переходных функци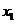й   и 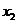 для звеньев 1 и 2 с указанными выше значениями параметров. Там же приведена расчётная переходная функция  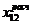для САУ, состоящей из двух апериодических звеньев 1 и 2, соединённых последовательно. С достаточной степенью точности её можно представить в виде экспоненты  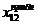с большой постоянной (в данном примере 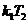), запаздывающей на малую постоянную ( ).

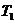    Звено 5 при 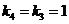, являющееся форсирующим звеном первого порядка с коэффициентом форсировки  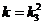и постоянной времени 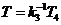,  может быть представлено в виде последовательного соединения двух звеньев:

– апериодического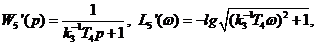

;

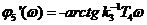– обратного апериодического (пропорционально-дифференцирующего) ,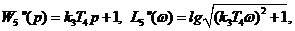

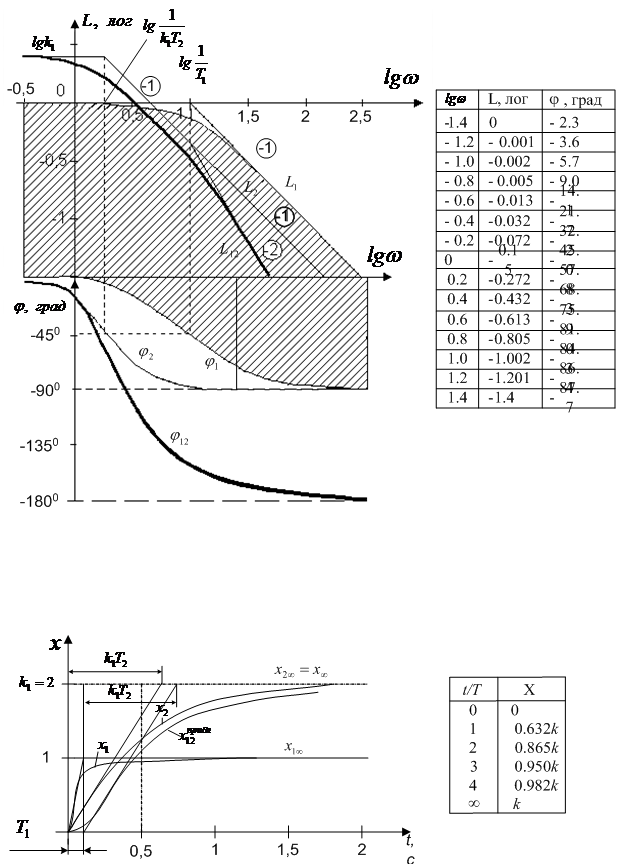
Рис. 2. ЛЧХ и переходные функции апериодических звеньев

с частотами сопряжения, соответственно,  и 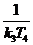. ЛАЧХ и ЛФЧХ  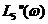и 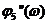 являющиеся зеркальным отображением относительно оси абсцисс прямого апериодического звена с постоянной времени 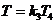, могут быть также построены с помощью шаблона. На рис. 3 представлены ЛЧХ составных часте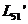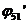й ,  и 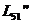, , 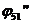а также ЛЧХ звена 5 в целом 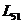,  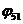при k₃>1; 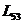,  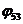– при k₃<1. Переходная функция звена 5 в этом случае описывается уравнением

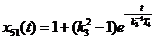                             ,                            (1.5)

(она представлена на рис. 3 в виде кривой x₅₁ для случая k₃=4).

При k₄=0, k₅=1 звено 5 является реальным дифференцирующим звеном первого порядка, т. е. вместо пропорционально-дифференцирующего звена будет идеально-дифференцирующее звено 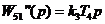. Переходная функция звена 5 в целом описывается в этом случае уравнением

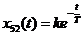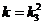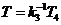                           , где ,                  (1.6)

(ЛЧХ( 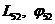), переходная функция  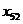и таблица расчета  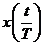представлены на рис. 3).

При 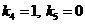 звено 5 является пропорционально-интегрирующим звеном, ЛЧХ которого (при k₃=0,5<1) представлено кривыми L₅₄, φ₅₄ на рис. 3.

 Переходная функция форсирующего звена может быть найдена по выражению

.

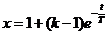На рис. 3 приведены

1) ЛАЧХ L₁, ЛФЧХ 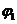 и переходная функция  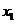для форсирующего звена с параметрами k₃ = 2  (k = 4), T₄ = 0,2 c  (T= 0,1 c);

2) ЛАЧХ L₂, ЛЧФХ 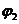 и переходная функция  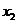для форсирующего звена с параметрами k₃ = 0,5  (k= 0,25), T₄ = 0,2 с ( T= 0,4 с);

3) при k₄ = 0, k₅ = 1 звено 5 является реальным дифференцирующим звеном 1-го порядка с коэффициентом форсировки 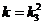 и постоянной времени 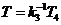. Переходная функция этого звена может быть найдена по выражению

                                 .

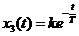На рис. 3 приведены ЛАЧХ L₃, ЛФЧХ 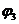, кривая и таблица с данными переходной функции 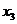реального дифференцирующего звена с параметрами   k₃ = 2  (k = 4), T₄ = 0,2 с (T= 0,1 c);

4) при k₄ = 1, k₅ = 0 звено 5 является пропорционально-интегрирующим звеном с коэффициентом усиления пропорциональной составляющей 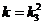 и постоянной интегрирования 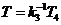. Его ЛАЧХ (при k₃=0,5<1) представлена кривыми 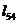,  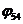на рис. 3. Переходная функция может быть найдена по выражению

                                 .

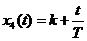На рис. 3 приведены ЛАЧХ L₄, ЛФЧХ j₄ и переходная функция  пропорционально-интегрирующего звена с параметрами k₃ = 0,5 (k = 0,25), Т₄ = 0,2 с  (Т = 0,4 с).

Во всех рассмотренных случаях наблюдается однозначная зависимость между формой ЛАЧХ и ЛФЧХ звеньев. Такие звенья и САУ, состоящая из этих звеньев, называются минимально-фазовыми.

При сопоставлении ЛАЧХ и соответствующих им переходных функций можно убедиться в следующем:

1) установившееся значение выходной величины определяется ординатой ЛАЧХ L(0) при нулевой частоте, т. е. 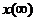= 10^L(0);

2) начальное значение выходной величины определяется ординатой ЛАЧХ при w = ¥, т. е. 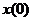= 10^L(¥);

3) переходный процесс протекает без перерегулирования, если ординаты ЛАХ на всех частотах не превышают ординаты ЛАХ при нулевой частоте;

4) максимум в ЛАХ свидетельствует о том, что переходный процесс протекает с перерегулированием. Максимальное отклонение выходной величины приблизительно равно входному сигналу, умноженному на максимальное значение коэффициента усиления амплитуды АЧХ (k_m=10^Lm);;

5) переходный процесс до достижения максимума протекает приблизительно по экспоненте, сдвинутой на время постоянного запаздывания. Экспонента имеет постоянную времени, которая определяется изменением наклона ЛАХ с нулевого (0) на единичный отрицательный (–1). Время постоянного запаздывания равно сумме постоянных времени, определяющих дальнейшее увеличение отрицательного наклона ЛАХ в области высоких частот;

6) переходный процесс после достижения максимума идёт приблизительно по экспоненте с постоянной времени, которая определяется изменением наклона аппроксимированной ЛАХ с единичного положительного (+1) на нулевой (0).

Построив 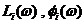 отдельных звеньев, результирующие  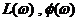при последовательном соединении в соответствии с формулой (1.1) получаются путём сложения ординат  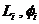при постоянной абсциссе 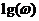. Варианты параметров в пределах одной бригады подобраны так, чтобы охватить основные виды результирующих ЛАЧХ САУ (рис. 4).

Определение показателей регулирования по результирующей ЛАЧХ минимально-фазовой САУ основано на построении приближённой кривой переходного процесса. При этом можно рекомендовать следующую методику:

1) построить аппроксимированную отрезками прямых с наклонами 1, 0, –1, –2, –3, … лог/дек результирующую ЛАЧХ системы. При этом будут получены аппроксимированные ЛАЧХ типа 1, 2, 3 (рис. 4);

2) определить частоты точек сопряжения отрезков с +1 и 0 наклоном 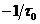, с 0 и –1 наклонами 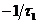, с –1 и –2 наклоном 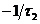и т.д.;

3) определить значения амплитуд, соответствующих максимальным и установившимся значениям ЛАЧХ ;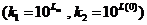

4) на оси времени кривой переходного процесса (рис. 5) отложить отрезок, соответствующий 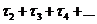, а из полученной точки на прямую k₁ отложить подкасательную τ₁ и соответствующей кривой нарастания x экспоненту;

5) для ЛАЧХ типа 1 кривая переходного процесса 1 может быть получена путём плавного перехода из начала координат на полученную экспоненту;

Рис. 3. ЛЧХ и переходные функции звена 5 

6) для ЛАЧХ типа 2 и 3 необходимо построить экспоненту с подкасательной 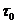, соответствующую спадающему участку кривой переходного процесса. Результирующая кривая 2, 3 переходного процесса может быть получена путём плавного перехода с нарастающего участка на экспоненту, соответствующую спадающему участку кривой переходного процесса до установившегося значения (k₂ , 0).

Определение основных показателей регулирования:

1) время регулирования 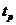 – это время достижения установившегося значения 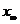с заданной точностью D (для силовых САУ обычно D = 0,05 или 0,02);

2) максимальное значение ;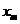

3) перерегулирование ;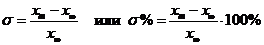

4) колебательность 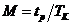, округлённое до целого,

где Т_K – период колебаний.

Последний показатель колебательности M определяется для замкнутых САУ или при наличии колебательных звеньев, т. е. в лабораторной работе № 1 M = 0.

При 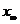= 0 перерегулирование смысла не имеет и поэтому не определяется.

Данные расчёта показателей регулирования заносятся в таблицу (рис. 4).

Вопросы для самоконтроля

1. Напишите передаточные функции, вычертите ЛАЧХ и переходные функции каждого динамического звена, используемого в работе.

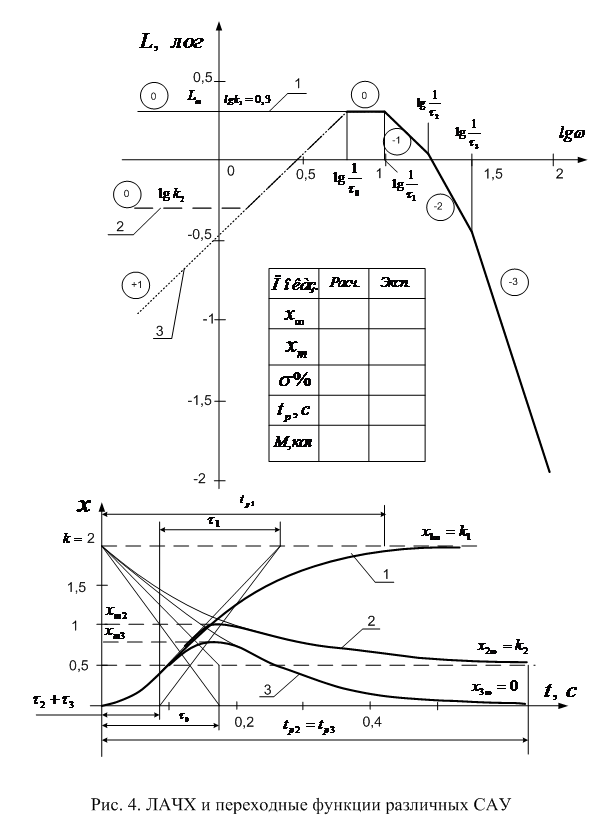
2. Приведите выражения передаточной функции, ЛАЧХ и ФЧХ при последовательном соединении звеньев.

 3. Каким значениям переходной функции соответствует L(ω= 0),        L(ω = ¥)?

4. О чём свидетельствует наличие всплеска в ЛАЧХ?

Литература

[1, c. 72–108, 125–141, 181–237];

[3, c. 51–88, 165–270];

[4, c. 45–74].

Мы поможем в написании ваших работ!