Итак, посевная площадь сахарной свеклы ежегодно увеличивалась в среднем на 10 га
Практическое занятие Анализ основной тенденции ряда динамики, построение сезонной волны
Цель:ознакомить студентов с правилами построения, основными приемами обработки и анализа рядов динамики, с методами выявления тенденции развития уровней ряда, моделирования и прогнозирования.
Задачи:рассмотреть требования, предъявляемые к уровням динамического ряда, порядок расчета цепных и базисных показателей динамики, их средних значений в единицу времени, особенности построения среднего уровня интервального и моментного рядов динамики, методики сглаживания и аналитического выравнивания, изучения сезонных колебаний и прогнозной экстраполяции.
Для всесторонней характеристики изменения социально-экономических явлений во времени расчета только одних показателей динамики и их средних величин не достаточно. В связи с этим статистика предлагает ряд специальных приемов обработки и анализа динамических рядов.
Важное место в изучении развития общественных явлений принадлежит сравнительному анализу нескольких рядов динамики. При этом можно сравнивать динамические ряды как одноименных, так и разноименных показателей, касающихся различных территорий или являются составными частями целого. Абсолютные уровни таких рядов динамики, как правило, вследствие различий методики исчисления показателей, денежной оценки продукции и других причин непосредственно несопоставимы. Поэтому целесообразно сравнивать не абсолютные, а относительные показатели и по ним делать выводы о том, какое явление и на какой территории возрастает (или снижается) быстрее. Этот прием получил название приведение рядов динамики к одному основанию, т.е. к общей базе сравнения, которую принимают за единицу или сто процентов.
|
|
|
Суть этого приема заключается в том, что данные о величине изучаемого показателя за год (или другой отрезок времени), взятый за базу сравнения принимают равным 100%, а на уровне отдельных лет (или других отрезков времени) сравнивают с ним, а долю выражают в процентах.
Практическое применение приема приведение рядов динамики к одному основанию рассматривается в следующем параграфе раздела учебника, посвященном факторном анализе рядов динамики (табл. 1 и 2).
В тех случаях, когда уровни ряда динамики за одни годы несопоставимы с уровнями за другие годы в связи с территориальными, ведомственными, организационными изменениями, изменением методики исчисления показателей или по другим причинами и возникает потребность обеспечить сопоставимость уровней, прибегают к смыкания динамических рядов, т.е. объединение двух и более рядов в один сомкнутый ряд.
|
|
|
Суть этого приема заключается в следующем. Уровне года, в течение которого произошли изменения, как до изменений, так и после изменений, берут за базу сравнения (обычно за 100%), остальные сравниваются с ним и выражают в процентах. В результате этого получим единый ряд относительных величин, характеризует изменение исследуемого явления за весь период.
Допустим, есть данные за 2004 - 2010 гг. по посевной площади картофеля в хозяйствах района, в территориальных границах которого в 2007 г. произошли изменения (табл. 1).
Анализ таблицы показывает, что в связи с изменением границ района в 2007 г. данные о посевную площадь картофеля за 2008 - 2010 гг. несопоставимы с данными за 2004 - 2006 гг. Чтобы иметь сопоставимые данные, выполним смыкания этих рядов динамики.
Таблица 1. Динамика посевной площади картофеля в хозяйствах района за 2004 - 2010 гг., га
| Пределы района | Годы | ||||||
| 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | |
| До изменений После изменений | 2100 | 2208 | 2315 | 2430 2686 | 2717 | 2804 | 2861 |
Смыкания рядов динамики и сведение их к сопоставимому виду осуществим двумя способами:
а) выражением ряда динамики в относительных показателях, приняв за базу сравнения один и тот же период;
|
|
|
б) пересчетом абсолютных показателей.
Смыкания рядов способом выражения рядов относительными показателями динамики выполним так. Возьмем год, в котором произошли территориальные изменения (в нашем примере это 2007 г.) за базу сравнения или 100%, а остальное уровней сравним с этим годом и полученные данные выразим в процентах. Следовательно, за 100% для первого ряда динамики (2004 - 2007 гг.) будет принята величина посевной площади картофеля, что составляет 2430 га, а для второго ряда динамики (2007 -2010 гг.) - 2686 га.Так, например, относительный показатель динамики посевной площади в 2001 г. по сравнению с 2007 г. составит 86,4% [(2100 :2430>100], в 2010 г. по сравнению с 2007 г, - 106,5% [(2861 : 2686) -100] и т.д.в Результате получим ряды относительных показателей динамики посевной площади картофеля с одинаковой базой сравнения, которые можно заменить одним сомкнутым рядом.
Смыкания рядов динамики способом пересчета абсолютных показателей осуществлен с помощью коэффициента пересчета (Кп), который определим как отношение двух уровней посевной площади после изменения границ района к посевной площади перед этим изменением:Перемножив посевную площадь картофеля первого ряда динамики (2004-2006гг.) на коэффициент пересчета, получим данные, которые сопоставлены с данными о посевную площадь картофеля второго ряда динамики ( 2008 - 2010гг.). Так, в 2004 г. посевная площадь картофеля в сопоставимом показателе равна 2320 га (2100-1,105), в 2005 г. - 2440 га (2208-1,105) и т.д.Все расчеты с приведения рядов динамики к сопоставимому виду сведем в табл.2.
|
|
|
Таблица 2. Сомкнутые ряды относительных и абсолютных изменений посевной площади картофеля в хозяйствах района за 2001 - 2010 гг.
| Год Показатель | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| 1.Относительные ряды, % | |||||||
| а) к изменению границ | 86,4 | 90,9 | 95,3 | 100,0 | - | - | - |
| б) после изменения границ | - | - | - | 100,0 | 101,2 | 104,4 | 106,5 |
| Сомкнутый ряд динамики, | |||||||
| полученный способом | |||||||
| расчета относительных | |||||||
| показателей динамики, % | 86,4 | 90,9 | 95,3 | 100,0 | 101,2 | 104,4 | 106,5 |
| Сомкнутый ряд динамики, полученный способом пересчета абсолютных показателей, га | |||||||
| 2320 | 2440 | 2558 | 2686 | 2717 | 2804 | 2861 |
Добытые сомкнутые ряды динамики позволяют сделать данные о посевную площадь картофеля за разные годы сопоставимыми, из них видно, что посевная площадь картофеля в районе как в абсолютных, так и в относительных показателях систематически росла.
Под влиянием случайных факторов (в сельскохозяйственном производстве к ним относят прежде всего метеорологические условия) уровни ряда динамики часто сильно колеблются по периодам времени, при этом тенденция развития затушевывается, наглядно не проявляется. В связи с этим одной из основных задач анализа рядов динамики является выявление основной тенденции развития социально-экономических явлений. Под общей тенденцией динамического рядапонимают тенденцию к росту, снижению или стабилизации уровня любого общественного явления.
Выявление тенденции в динамических рядах дает возможность оценить характер развития исследуемого явления, определить эффективность факторов, формирующих основную тенденцию, установить уровни исследуемого явления на перспективу.
Выявление основной тенденции изменения уровней динамического ряда предусматривает ее количественное выражение, в некоторой мере свободной от случайных причин. Это достигается путем абстрагирования от индивидуальных, случайных изменений признаки. Выявление основной тенденции развития (тренда) называется в статистике также выравниванием временного ряда, а приемы выявления основной тенденции - приемами выравнивания. Выравнивание позволяет охарактеризовать особенности изменения во времени данного динамического ряда в наиболее общем виде как функцию времени, предполагая, что через время можно выразить влияние основных факторов.
В практике экономического анализа нередки случаи, когда общая тенденция явления к росту или снижению проявляется достаточно четко. Приведены данные о динамике поголовья коров (табл. 3) показывают, что в динамическом ряду имеет место общая тенденция к росту поголовья коров. Однако для выявления тенденции в рядах динамики не достаточно одного визуального анализа ряда, если его уровне за любые объективные или случайные причины существенно колеблются, то возрастая, то снижаясь. Это затушевывает, наглядно не проявляет основную тенденцию развития явления. Например, если урожайность любой сельскохозяйственной культуры под влиянием метеорологических условий, действующих в разных направлениях, очень колеблется по годам, то основная тенденция изменения урожайности может не проявляться непосредственно. В таких случаях для проявления основной тенденции нужно прибегнуть к специальным приемам обработки динамических рядов.К таким приемам относятся укрупнение периодов, сглаживание ряда динамики способом скользящей средней, выравнивание ряда динамики по среднему абсолютному приросту, среднему коэффициенту роста и способа наименьших квадратов (аналитическое выравнивание рядов динамики).Рассмотрим на конкретных примерах условия и технику выявления основной тенденции развития динамических рядов каждым из названных приемов.
Одним из самых простых приемов выявления тенденции развития является прием укрупнения периодов. Суть его заключается в том, что абсолютные или средние уровни ряда динамики за короткие интервалы времени (год, месяц, декаду, день и т.д.), испытывающих случайных колебаний, заменяющих обобщающим (обычно средним) значением за более длительный период (трехлетие, пятилетие и т.д.).По сути способом укрупнения периодов представляет собой типологическое группирование уровней ряда динамики, поэтому при его применении необходимо придерживаться научных основ построения статистических группировок.При укрупнении периодов очень важно научно обоснованно и правильно выделить периоды времени для укрупнения. Периоды, что их выделяют, должны быть однородными в качественном отношении и достаточно длительными по времени, чтобы произошло погашение случайных колебаний явления.Применение этого приема, как правило, связывается с использованием равных по продолжительности периодов. Однако продолжительность периодов может быть различной. Выделение неравных периодов предопределяется наличием качественных специфических периодов в развитии того или иного социально-экономического явления.
Покажем порядок расчета укрупненных периодов, используя данные об урожайности подсолнечника за 15 лет (табл. 4).
Таблица 4. Динамика урожайности подсолнечника в ООО района за 1996- 2010 гг.
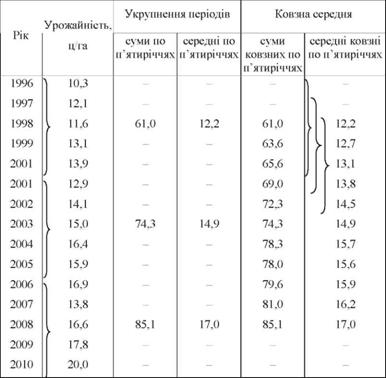 Обоснуем продолжительность укрупненных периодов для нашего примера. Анализ исходного ряда динамики показывает, что каких-либо качественных периодов или периодических колебаний внутри динамического ряда урожайности за исследуемый период не наблюдается.Как показывает анализ исходного ряда динамики, урожайность в хозяйствах района изменяется постепенно, тенденция ее изменения затушевывается в отдельные годы главным образом метеорологическими условиями. Поскольку влияние метеорологических условий для исследуемой зоны в большинстве случаев выравнивается по пятилетних периодах, укрупнение осуществлено по п'ятиріччях. Благодаря такому укрупнению взаємопогасяться случайные факторы и окажется общая тенденция изменения урожайности.Чтобы получить средние уровни по п'ятиріччях, сначала найдем суммы урожайности за каждое пятилетие (1996 - 2000 гг., 2001 - 2005гг., 2006 - 2010 гг.), а потом добытые суммы делим на количество лет в укрупненном периоде (пять).
Обоснуем продолжительность укрупненных периодов для нашего примера. Анализ исходного ряда динамики показывает, что каких-либо качественных периодов или периодических колебаний внутри динамического ряда урожайности за исследуемый период не наблюдается.Как показывает анализ исходного ряда динамики, урожайность в хозяйствах района изменяется постепенно, тенденция ее изменения затушевывается в отдельные годы главным образом метеорологическими условиями. Поскольку влияние метеорологических условий для исследуемой зоны в большинстве случаев выравнивается по пятилетних периодах, укрупнение осуществлено по п'ятиріччях. Благодаря такому укрупнению взаємопогасяться случайные факторы и окажется общая тенденция изменения урожайности.Чтобы получить средние уровни по п'ятиріччях, сначала найдем суммы урожайности за каждое пятилетие (1996 - 2000 гг., 2001 - 2005гг., 2006 - 2010 гг.), а потом добытые суммы делим на количество лет в укрупненном периоде (пять).
Найденные суммы и средние запишем центруючи их на середину каждого пятилетия (соответственно в 1998 г., 2003 г. и 2008 г.).В результате проведенного укрупнения периодов ряда динамики четче проявляется тенденция роста урожайности за годы, анализируются. Так, добытые результаты показывают, что от пятилетия к пятилетию урожайность подсолнечника в TOB района систематически возрастала (с 12,2 ц/га в 1996 - 2000 гг. до 17,0 ц/га в 2006 - 2010 гг., то есть на 4,8 ц/га, или на 39,3%).При укрупнении периодов число членов динамического ряда очень сокращается. Этот существенный недостаток в значительной мере устраняется при использовании приема выравнивания динамических рядов способом скользящих средних.Этот способ также основан на укрупнении периодов. Суть расчета скользящих средних заключается в том, что состав периода непрерывно и постоянно меняется - происходит сдвиг на одну дату при сохранении постоянного интервала периода (трехлетие, пятилетие и т.д.).
Скользящая средняя - это средняя укрупненных периодов, созданных последовательным исключением каждого начального уровня интервала и замены его очередным последующим уровнем ряда. Таким образом, происходит как бы скольжение периода и полученной средней по динамическому ряду. Например, при згладжувані по триріччях
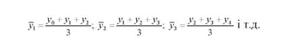
Этот прием, как и предыдущий, основывается на известном теоретическом положении о том, что в средних величинах взаимно погашаются случайные отклонения и оказывается типичное, закономерное.При выявлении тенденции приемом скользящих средних, так же как и при использовании приема укрупнения периодов, одним из важных вопросов является вопрос о продолжительности периодов. Интервал должен быть достаточно большим и обеспечить взаимное погашение случайных отклонений уровней. Если в развитии явления имеет место цикличность (периодичность), то интервал скольжения следует принимать равным длительности цикла. Чем дольше интервал скольжения, тем в большей степени выравнивается ряд в результате усреднения исходных уровней.Покажем порядок расчета скользящих средних, используя данные об урожайности подсолнечника (табл. 4).nСкользящие средние рассчитаем также по пятилетним периодам. Для расчета скользящих средних подытожим урожайность за первые пять лет (1996 - 2000 гг.).а затем, опуская данные первого в ряду динамики года, подытожим урожайность за следующее пятилетие (1997 - 2001 гг.) и т.д. Происходит как бы скольжение по ряду динамики. Добытые суммы разделим на число лет в периоде скольжения (пять), а вычисленную среднюю отнесем к середине периода скольжения (в нашем примере третий год каждого пятилетнего периода скольжения).Рассчитаны скользящие средние показывают устойчивую тенденцию роста урожайности подсолнечника в TOB района.Скользящая средняя сглаживает вариацию уровней, но не дает ряда динамики, в котором все выходные уровни были бы заменены выровненными. Это объясняется недостатком выравнивание ряда способом скользящей средней, при котором выровненный ряд "сокращается" по сравнению с исходным на (n - rm):2 члена с одного и второго конца (под п понимают число членов, из которых определяют скользящие средние).Стремление в процессе выравнивания ряда заменить все выходные уровни заголовков обуславливает применение более совершенных приемов выравнивания рядов динамики. К таким приемам относятся: выравнивание по среднему абсолютному приросту, среднему коэффициенту роста и способа наименьших квадратов.В основе применения способа выравнивания ряда динамики по среднему абсолютному приросту лежит предположение, что каждый следующий уровень изменяется по сравнению с предыдущим примерно на одинаковую величину, равную среднему абсолютному приросту.
Уравнения, отражает тенденцию развития явления за этим способом выравнивания ряда динамики имеет вид:
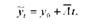
где - выровненные уровни ряда динамики;
у0 - начальный уровень ряда динамики;
А - средний абсолютный прирост;
и - порядковый номер даты (и = 1,2,3,...,п).
Технику выявления тенденции на основе среднего абсолютного прироста рассмотрим на примере динамического ряда посевной площади сахарной свеклы (табл. 5).Анализ ряда динамики показывает, что для него характерно постоянное увеличение посевной площади сахарной свеклы. При этом ежегодные абсолютные приросты посевной площади стабильны и составляют около 10 га. Наиболее приемлемым способом выравнивания рядов динамики, которые имеют постоянные абсолютные приросты, является способ выравнивания рядов по среднему абсолютному приросту.
Таблица5. Динамика посевной площади сахарной свеклы в хозяйстве за 2005 - 2010 гг.

Итак, посевная площадь сахарной свеклы ежегодно увеличивалась в среднем на 10 га.
Определим выровнены по среднему абсолютному приросту значения посевной площади для каждого года, подставляя в уравнение вместо и значение:
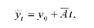
где и - порядковый номер года (i = 0,1,2,3,4,5). Выровненные значения посевной площади составят:
в 2005 г. (прии = 0) у = у0 + Ли, = 250 + 10-0 = 250 га;
в 2006 г. (при t = 1~t = y0 + At,=250 + 10-1 = 260 rai т.д. Выравнивание по среднему абсолютному приросту ряд динамики на графике представляет собой прямую линию, которая соединяет минимальное и максимальное значение. Как видно из таблицы, отклонения фактических уровней от выровненных незначительные. Итак, выравнивание ряда динамики по среднему абсолютному приросту позволило точнее отразить тенденцию изменения посевной площади сахарной свеклы в хозяйстве.в то же Время необходимо отметить, что теоретическая линия, которая выравнивает ряд динамики, целиком зависит только от двух крайних значений уровней ряда динамики (начального и конечного), которые могут существенно изменяться под влиянием случайных колебаний. В соответствии тенденция, которая действительно имеет место в исследуемом явлении, будет искажена. В связи с этим прием выравнивания рядов динамики по среднему абсолютному приросту целесообразно использовать только для рядов, имеющих стабильные ежегодные абсолютные приросты. Практически этот прием используется в динамических рядах, которые охватывают непродолжительный период времени, в течение которого не происходит существенных качественных изменений в уровнях факторов, определяющих тенденцию, и степени их влияния на изучаемый признак.
Выравнивание ряда динамики по среднему коэффициенту роста применяется в тех случаях, когда в исследуемом ряду каждый следующий уровень изменяется по сравнению с предыдущим примерно в одно и то же количество раз, равное величине среднего коэффициента роста, то есть когда факторы, определяющие основную тенденцию обусловливают от периода к периоду одинаковые коэффициенты роста исследуемого явления.
Выровненные значения уровней ряда динамики определяют по формуле:
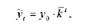
где к - средний коэффициент роста.
Порядок выравнивания по среднему коэффициенту роста рассмотрим на примере динамикифондозабезпеченості (табл. 9).
Таблица 9. Динамика стоимости основных производственных фондов животноводства в ООО за 2005 - 2010 гг.
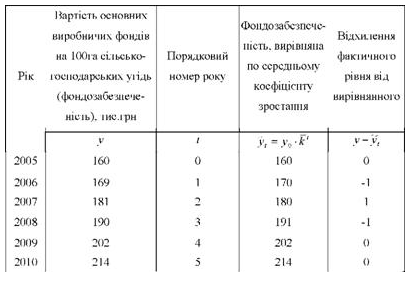
Анализ динамического ряда показывает, что абсолютные приросты увеличиваются от 9 - 10 тыс. грн. в первые годы до 12 тыс. грн. в последние годы, а коэффициенты роста остаются примерно одинаковыми и составляют 1,06 - 1,07. Следовательно, для данного динамического ряда характерно увеличение каждого следующего уровня по сравнению с предыдущим в то же количество раз, равное величине среднего коэффициента роста. Поэтому данный ряд динамики целесообразно выравнивать по среднему коэффициенту роста.
Определим средний коэффициент роста фондозабезпеченості по формуле:
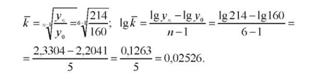
По таблицам антилогарифмов установим значение к = 1,06.
Итак, фондообеспеченность хозяйства ежегодно в среднем росла в 1,06 раза, или на 6,0%.
Вычислим выровненные по среднему коэффициенту роста значения фондозабезпеченості:
в 2005 г. (при X = 0) = у0 ■ к' = 160-1,06° = 160 тыс. грн;
в 2006 г. (при X = 1) у, = у0 ■ к' = 160-1,061 = 170 тыс. грн и т.д.
Следует иметь в виду, что при определении выровненных значений уровней ряда динамики по среднему коэффициенту роста, так же как и при выравнивании по среднему абсолютному приросту, в исходном и выровненном рядах динамики начальные и конечные уровни совпадают.
Выравнивание по среднему коэффициенту роста ряд динамики представляет собой показникову кривую. Этому способу выравнивания рядов динамики присущ тот же недостаток, что и выравниванию по среднему абсолютному приросту. Здесь при определении выровненных значений используются только два крайних уровни динамического ряда (начальный и конечный), которые вследствие влияния случайных факторов могут быть нехарактерными для исследуемого общественного явления.
Дата добавления: 2018-04-04; просмотров: 263; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
