Лабораторная работа №2. Закон Густафсона-Барсиса
Содержание
1 Лабораторная работа №1..................................................................................2
2 Лабораторная работа №2..................................................................................4
3 Лабораторная работа №3..................................................................................6
Лабораторная работа №1. Закон Амдала.
Постановка задачи
Исследовать изменения производительности многопроцессорных систем в соответствии с законом Амдала.
Эксперимент 1. Необходимо построить и произвести анализ двух графиков зависимости (1.2) при S=const (часть операций, для которых возможно только последовательное выполнение), S<1, cоответственно, подлежащим распараллеливанию операциям остается часть задачи, равная (1-S). N=var, причем для первого графика S=S1, а для второго S=S2. N0 и Nk – соответственно, начальное и конечное число процессоров при вычислениях, а dN – шаг изменения для параметра N. В качестве вычислительной среды рекомендуется cистема MathCad.
Эксперимент 2. Необходимо построить и произвести анализ двух графиков зависимости при S=var, N=const, причем для первого графика N=N1, а для второго N=N2. S0 и Sk – соответственно, начальная и конечная величина параметра S при вычислениях, а dS – шаг его изменения.
Для варианта №5 данные следующие:
| Задание | Эксперимент 1:
S=const, N=var | Эксперимент 2: N=const, S=var | ||||||||
| Вариант | S1;S2 | N0 | dN | Nk | N1;N2 | S0 | dS | Sk | ||
| 16 | 0.4;0.6 | 160 | 100 | 10000 | 500;800 | 0.4 | 0.005 | 0.9 | ||
Ход работы
Для выполнения экспериментов 1 и 2 в среде MathCad были составлены два документа, в которых был произведен расчет изменения производительности и построен график.
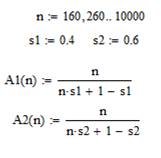
Рисунок 1.1 – Документ MathCad для вычислительного эксперимента 1
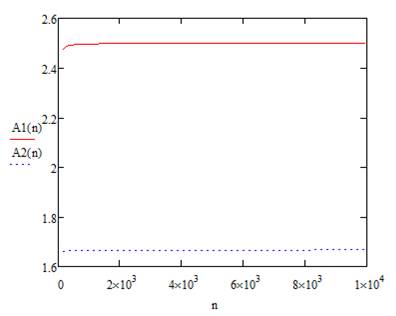
Рисунок 1.2 – Графики зависимости Ai(n) для эксперимента 1
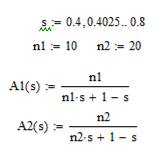
Рисунок 1.3 – Документ MathCad для вычислительного эксперимента 2
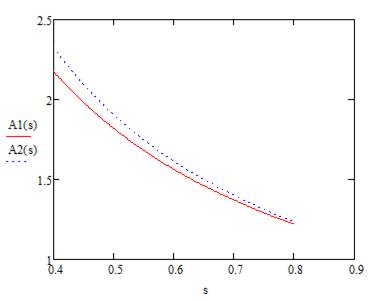
Рисунок 1.4 – Графики зависимости A(N,S) для задания 2
Контрольные вопросы
1. Что констатирует закон Амдала.
Закон Амдала показывает, что прирост эффективности вычислений зависит от алгоритма задачи и ограничен сверху для любой задачи без параллельных вычислений. Не для всякой задачи имеет смысл наращивание числа процессоров в вычислительной системе.
2. Определить следствия закона Амдала.
- последовательная часть накладывает строгие ограничения на ускорение, которое может быть достигнуто путем увеличения числа процессоров;
- построение системы с большим числом процессоров неэффективно, поскольку достаточное ускорение при этом не достигается;
|
|
|
- с другой стороны, большинство важных приложений, нуждающихся в распараллеливании, содержат очень незначительную долю последовательных вычислений и в этом случае системы с большим числом процессоров вполне обоснованы.
3. В каких единицах измеряется производительность суперЭВМ.
ФЛОПС - внесистемная единица, используемая для измерения производительности компьютеров, показывающая, сколько операций с плавающей запятой в секунду выполняет данная вычислительная система.
4. Что понимается под масштабируемостью высокопроизводительных вычислительных систем.
Масштабируемость представляет собой возможность наращивания числа и мощности процессоров, объемов оперативной и внешней памяти и других ресурсов вычислительной системы. Масштабируемость должна обеспечиваться архитектурой и конструкцией компьютера, а также соответствующими средствами программного обеспечения.
5. Чему равен 1 ТFlops.
10 в 12 степени операций в секунду.
Вывод
В результате проведенных экспериментов были исследованы изменения производительности многопроцессорных систем в соответствии с законом Амдала, который позволяет оценить производительность многопроцессорной вычислительной системы в зависимости от числа процессоров и степени распараллеливания вычислительного процесса.
|
|
|
Закон Амдала констатирует, что максимальный прирост производительности ограничен относительным числом операций, которые должны быть выполнены последовательно, то есть последовательной частью алгоритма. Он зависит от количества процессоров и доли последовательных операций в программе, причем зависимость эта не линейна.
В первом эксперименте мы последовательно увеличивали число процессоров n, при этом количество задач s1=0.4 и s2=0.6. На графике кривые имеют небольшойсильное расхождение Во втором эксперименте мы последовательно увеличивали число задач S, оставляя без изменений количество процессоров N. При этом кривые A(n1) и A(n2) в случае с n1=10 и n2=20 практически совпадают и показывают отрицательную динамику.
Из построенных графиков мы видим, что построение вычислительной системы с большим числом процессоров не всегда эффективно, поскольку достаточный прирост производительности при этом не достигается. При этом увеличение количества последовательно выполняемых задач оказывает существенное влияние на производительность вычислительной системы, так как замедляет ее работу.
|
|
|
Лабораторная работа №2. Закон Густафсона-Барсиса.
Постановка задачи
Провести исследование изменения производительности многопроцессорных вычислительных систем согласно закону Густафсона-Барсиса и сравнить результаты исследований с результатами для закона Амдала.
Эксперимент 1. Необходимо построить и произвести анализ двух графиков зависимости (3.1) при S=const, N=var, причем для первого графика S=S1, а для второго S=S2. N0 и Nk – соответственно, начальное и конечное число процессоров при вычислениях, а dN – шаг изменения для параметра N. В качестве вычислительной среды рекомендуется cистема MathCad.
Эксперимент 2. Необходимо построить и произвести анализ двух графиков зависимости (3.1) при S=var, N=const, причем для первого графика N=N1, а для второго N=N2. S0 и Sk – соответственно, начальная и конечная величина параметра S при вычислениях, а dS – шаг его изменения.
Ход работы
- Для выполнения экспериментов 1 и 2 необходимо в среде MathCad составить два документа;
- произвести расчет изменения производительности и построить график;
- произвести анализ полученных результатов и сделать выводы об изменении прироста производительности;
- аналогично провести вычислительный эксперимент 2;
- сравнить результаты работ 1 и 2.
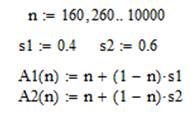
Рисунок 2.1 – Документ MathCad для вычислительного эксперимента 1
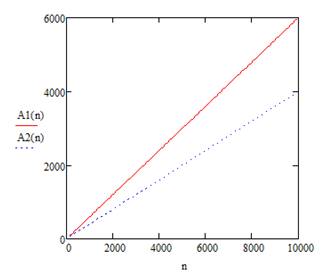
Рисунок 2.2 – Графики зависимости A(N,S) для задания 1
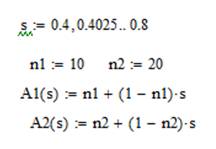
Рисунок 2.3 – Документ MathCad для вычислительного экперимента 2
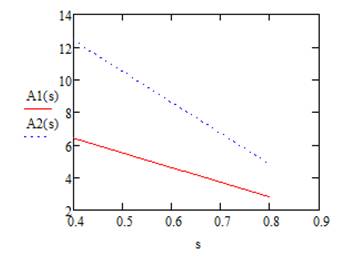
Рисунок 2.4 – Графики зависимости A(N,S) для задания 2
Контрольные вопросы
1.Что констатирует Закон Густафсона-Барсиса.
Данная характеристика показывает, насколько эффективно могут быть организованы параллельные вычисления при увеличении сложности решаемых задач
2. Существует ли противоречие в законах Амдала и Густафсона-Барсиса.
Не противоречит закону Амдала, тк показывает эффективность вычислений при увеличении сложности, до максимально-допустимой точки.
3. Чему равен один PFlops.
10 в 15 степени операций в секунду.
4. Для чего предназначена библиотека функций MPI.
Программный интерфейс (API) для передачи информации, который позволяет обмениваться сообщениями между процессами, выполняющими одну задачу. Необходим для распараллеливания процессов.
5. Дайте определение постулату Флинна.
все компьютеры делятся на четыре класса в зависимости от числа потоков команд и данных.
6. Назначение пакета программ LINPACK.
программная библиотека, написанная на языке Фортран, которая содержит набор подпрограмм для анализа и решения плотных систем линейных алгебраических уравнений. Также используется для определения вычислительных мощностей процессоров.
Вывод
Данный график, в отличие от графика, построенного на основе закона Амдала, показывает, что при увеличении количества процессоров линейный прирост производительности возможен за счет увеличения сложности решаемой задачи (организация параллельных вычислений, линейное увеличение программного кода).
Наглядно видно, что чем S ближе к 1, тем меньший прирост производительности дает увеличение количества процессоров, т.к. слишком большое число последовательно выполняемых процессов.
Лабораторная работа № 3.
Дата добавления: 2018-04-04; просмотров: 781; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
