Показатели рядов распределения
Структурные характеристики вариационного ряда распределения
Понятие и виды статистических рядов
Результаты статистических сводок и группировок могут быть представлены в виде статистических рядов – упорядоченных совокупностей значений показателей (статистического признака). По своему содержанию статистические ряды подразделяются на ряды динамики и ряды распределения. Ряд распределения, представляет собой систематизированную последовательность статистических единиц, сгруппированных по конкретному признаку. Он характеризует состав изучаемого явления, позволяет судить об однородности совокупности, закономерности распределения статистических единиц. Обычно ряд распределения представляет собой результат структурной группировки. Ряд распределения считается построенным, если известно, каким образом меняются в совокупности значения признака и как часто встречаются отдельные значения признака.
Для различных статистических признаков строятся ряды распределения разного типа:
• атрибутивные – строятся по описательным признакам в порядке возрастания или убывания наблюденных значений признака; примером атрибутивных рядов могут служить распределения населения по национальности, по профессиям, по полу; распределение предприятий по формам собственности;
• вариационные - строятся по количественным признакам, например, распределение рабочих по уровню квалификации, по заработной плате, распределение студентов по успеваемости.
|
|
|
Вариационные ряды делятся на дискретные и интервальные. В дискретных рядах признак принимает только целые значения, например, размер семьи, тарифный разряд. Интервальные ряды основаны на непрерывных признаках, принимающих любые, в том числе и дробные значения. В зависимости от того, какая структурная группировка лежит в основе интервального ряда, различают равноинтервальные и неравноинтервальные ряды. В равноинтервальных рядах ширина интервала является величиной постоянной, в неравноинтервальных – она различна для разных групп.
Для отображения процессов развития, движения социально-экономических явлений во времени строятся ряды динамики (хронологические, временные, динамические ряды), представляющие собой последовательность упорядоченных во времени значений статистического показателя.
Любой ряд динамики состоит из двух элементов:
1. показатель времени ti - это моменты или периоды времени, к которым относятся числовые значения показателей;
2. уровень ряда yi , под которым понимается значение статистического показателя, относящееся к определенному моменту или периоду времени.
|
|
|
Каждый ряд динамики может быть представлен в табличной форме - в виде пар значений t и y; и в графической форме - в виде линейной диаграммы.
С помощью рядов динамики в статистике решают следующие задачи:
• Получение характеристик интенсивности изменения явления во времени и характеристик отдельных уровней;
• Выявление и количественная оценка основной долговременной тенденции развития явления;
• Изучение периодических и сезонных колебаний явления;
• Экстраполяция и прогнозирование.
При обработке статистических данных используются ряды динамики, различающиеся по следующим признакам: по времени, форме представления уровней, числу показателей, по расстоянию между датами или интервалами. По времени различают моментные и интервальные ряды динамики. В моментных рядах уровни выражают состояние явления на критический момент времени. Особенностью моментного динамического ряда является то, что сумма членов ряда не имеет реального смысла. Например, численность населения, численность работающих и т.д. В таких рядах каждый последующий уровень полностью или частично содержит значение предыдущего уровня, поэтому суммировать уровни нельзя, так как это приводит к повторному счету.
|
|
|
В интервальных – уровни отражают состояние явления за определенный период времени – сутки, месяц, год и т.д. Это ряды показателей объема производства, объема продаж по месяцам года, количества отработанных человеко- дней и т.д. Уровни интервального ряда можно суммировать.
По форме представления уровней различают ряды абсолютных, относительных и средних величин. По числу показателей выделяют изолированные и комплексные ряды динамики (многомерные). Изолированный ряд строится по отдельному показателю, комплексный – по системе взаимосвязанных показателей.
По расстоянию между датами или интервалами ряды динамики делятся на ряды с равноотстоящими и неравноотстоящими уровнями. В рядах с равноотстоящими уровнями расстояние между датами или периодами одинаково, в рядах с равноотстоящими уровнями – оно различно.
Следует помнить о требовании сопоставимости уровней рядов динамики. Они должны относиться к одинаковой территории, включать одинаковый круг объектов, выражаться одинаковыми единицами измерения, рассчитываться до единой методологии.
Показатели рядов распределения
Основными элементами рядов распределения являются:
|
|
|
1) значение признака (варианта):
2) частота (n) - число единиц совокупности, обладающих данным значением признака. Частота показывает, сколько раз данное значение признака встречается в совокупности; сумма всех частот всегда равна объему статистической совокупности.
Она является исходной характеристикой любого ряда распределения. На ее основе можно рассчитать и другие характеристики:
Частость (q) – удельный вес (доля) единиц совокупности, имеющих определенное значение признака, т. е. это частота, выраженная в виде относительной величины (доли единицы или процента).
Накопленная частота (N) – число единиц совокупности, у которых значение признака не превышает данного, т. е. это частота нарастающим итогом:
Накопленная частость (Q) – удельный вес (доля) единиц, у которых значениепризнака не превосходит данное, т. е. это частость нарастающим итогом:
Плотность распределения – универсальная частотная характеристика, позволяющая перейти от эмпирического к теоретическому распределению. Длярядов с неравными интервалами только эта характеристика дает правильноепредставление о характере распределения. Плотность распределения рассчитывается в 2-х вариантах:
- как абсолютная плотность распределения


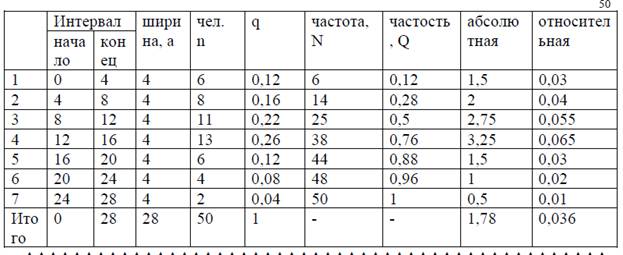
Графики являются наглядной формой отображения рядов распределения. Для изображения рядов применяются линейные графики и плоскостные диаграммы, построенные в прямоугольной системе координат. Для графического представления атрибутивных рядов распределения используются различные диаграммы: столбиковые, линейные, круговые, фигурные, секторные и т. д. Для дискретных вариационных рядов графиком является полигон распределения. Для анализа рядов распределения широко используются средние показатели ипоказатели вариации.
Для характеристики положения центра ряда распределения можно использовать 3 показателя: среднее значение признака, мода, медиана.
При выборе вида и формы конкретного показателя центра распределения необходимо исходить из следующих рекомендаций:
• для устойчивых социально-экономических процессов в качестве показателя


S – накопленная частота интервала, предшествующего интервалу, содержащему данный квартиль
Основные структурные показатели вариационного ряда, мода; медиана; квартили; децили.
Мода - это наиболее часто встречающееся в совокупности значение признака. Для дискретного вариационного ряда мода определяется по частотам вариант и соответствует варианте с максимальной частотой.
Особенности применения моды:
1) если все значения вариационного ряда имеют одинаковую частоту, то говорят, что этот вариационный ряд не имеет моды;
2) если две соседних варианты имеют одинаковую доминирующую частоту, то мода вычисляется как среднее арифметическое этих вариант;
3) если две несоседних варианты имеют одинаковую доминирующую частоту, то такой вариационный ряд называется бимодальным;
4) если таких вариант более двух, то ряд полимодальный.
Определение модального интервала в случае интервального вариационного ряда:
1) с равными интервалами модальный интервал определяется по наибольшей частоте;
2) при неравных интервалах - по наибольшей плотности.
Применение моды:
1) в практике мода и медиана иногда используются вместо средней арифметической или вместе с ней;
2) фиксируя средние цены товаров или продуктов на рынке, записывают наиболее часто встречающуюся цену на рынке (моду цены).
Медиана - это значение изучаемого признака, приходящееся на середину ранжированной совокупности.
Порядок вычисления медианы:
при вычислении медианы интервального вариационного ряда сначала находят медианный интервал l*u I хы +h\, где Л - длина медианного интервала. Для этого можно использовать кумулятивное распределение частот или относительных частот. Медианному интервалу соответствует тот, в котором содержится накопленная частота, равная 1/2;
Применение свойства медианы:
при проектировании оптимального положения остановок общественного транспорта; при проектировании складских помещений; при сооружении бензозаправок и т. д.
Особенности вычисления квартили:
первый квартиль (нижний) отделяет четверть ранжированной совокупности снизу
Медиану можно рассматривать как второй квартиль.
Для изучения характера вариации используются средние значения разных степеней отклонений отдельных величин признака от его средней арифметической величины. Эти показатели называют центральными моментами распределения порядка, соответствующего степени, в которую возводятся отклонения. Согласно свойству средней арифметической центральный момент первого порядка равен нулю, второй центральный момент представляет собой дисперсию. Величина третьего момента m3:зависит, как и его знак, от преобладания положительных отклонений в кубе над отрицательными либо наоборот.
При нормальном и любом другом строго симметричном распределении сумма положительных отклонений в кубе строго равна сумме отрицательных отклонений в кубе.
Момент третьего порядка используется при оценке асимметрии.
В анализе вариационных рядов применяются также специальные показатели, позволяющие охарактеризовать расхождения между эмпирическим и нормальным распределениями как с качественной, так и с количественной стороны. Нормальное распределение строго симметрично. Фактически распределения, построенные по эмпирическим данным, как правило, асимметричны, т. е. смещены по отношению к оси симметрии нормального распределения влево или вправо. Для определения направления величины этого смещения (скошенности) употребляется коэффициент асимметрии:
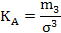
где m3- центральный момент третьего порядка;
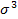 - куб среднего квадратического отклонения.в эмпирических распределениях центральный момент нечеткого порядка будет отличаться от нуля в зависимости от характера асимметрии: при левосторонней асимметрии он будет меньше нуля, при правосторонней - больше нуля. Коэффициент асимметрии позволяет проводить сравнения между собой различных распределений.
- куб среднего квадратического отклонения.в эмпирических распределениях центральный момент нечеткого порядка будет отличаться от нуля в зависимости от характера асимметрии: при левосторонней асимметрии он будет меньше нуля, при правосторонней - больше нуля. Коэффициент асимметрии позволяет проводить сравнения между собой различных распределений.
На основе разности между средней величиной и модой вычисляют другой показатель асимметрии:
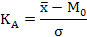
который при левосторонней асимметрии отрицателен, а при правосторонней - положителен.
Дата добавления: 2018-04-04; просмотров: 3497; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
