Синтез та моделювання роботи двійково-десяткового суматора
Лабораторна робота № 2
Синтез і моделювання роботи двійково-десяткового суматора та порівнювача двійкових кодів
Мета роботи: вивчення методів проектування (синтезу) цифрових пристроїв комбінаційного типу, вибір елементної бази та побудова принципових схем. Спрощення булевих виразів на основі карт Карно. Реалізація двійково-десяткових суматорів, порівнювачів двійкових кодів і перевірка їх роботи з допомогою САПР Elektronics Workbench.
Теоретична частина
Будь-який логічний вираз, складений з 
логічних змінних 
з допомогою скінченого числа операцій булевої алгебри, можна розглядати як деяку функцію змінних. Функція може приймати в залежності від значень змінних тільки два значення: 
та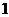 
. Такі функції є зручним інструментом для аналізу та синтезу логічних схем, вихідні сигнали яких характеризуються лише двома рівнями напруги: високим ( 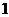) та низьким ( ). Тому такі функції ще називаються функціями переключення.
Таблиця, що містить всі можливі комбінації значень вхідних змінних разом з відповідними їм значеннями вихідних змінних (значеннями функцій) називається таблицею істинності. Для вхідних змінних таблиця містить 
рядків та 
стовбців, як показано в табл. 2.1.
Табл. 2.1
| 
| … | 
| 
| 
|
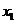
| 0 | 0 | … | 0 | 0 | 
|
| 0 | 0 | … | 0 | 1 | 
|
| … | … | … | … | … | … |
| 1 | 1 | … | 1 | 1 | 
|
Як таблиці істинності так і логічні функції використовуються для опису логічних схем. Оскільки вони описують одну і ту ж схему, необхідно вміти переходити від однієї форми опису до іншої.
|
|
|
З таблиці істинності можна одержати логічну функцію у вигляді двох форм: суми добутків – диз’юнктивна нормальна форма (ДНФ) та добутку суми – кон’юнктивна нормальна форма (КНФ). Будь-яка логічна функція може мати декілька ДНФ або КНФ. Однозначність функції переключення можлива при записі її в досконалих нормальних формах. Досконалі нормальні форми функції переключення отримують з допомогою таблиць істинності цієї функції. Досконала диз’юнктивна нормальна форма (ДДНФ) представлення функії переключення – запис функції у вигляді диз’юнкції кон’юнкцій, для яких значення функції рівне 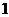. При повному наборі значень змінних такі кон’юкції рівні 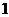і називаються мінтермами.
Досконала кон’юнктивна нормальна форма (ДКНФ) - представлення функції переключення у вигляді кон’юнкції диз’юнкцій для яких значення функції рівне нулю. Кожна диз’юнкція цієї кон’юнкції включає кожну змінну тільки один раз в прямому або інверсному вигляді. При повному наборі значень змінних такі диз’юнкції рівні нулю і носять назву макстермів.
Для логічних змінних число мінтермів 
та макстармів 
однакове і рівне 
. Кількість змінних, які містяться в логічному виразі (мінтермі або макстермі), називається рангом.
|
|
|
Розглянемо побудову логічної функції у ДДНФ на прикладі конкретної таблиці істинності (табл. 3.2).
Табл. 2.2
| 
| 
| 
|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Перший рядок табл. 2.2, в якій функція має одиничне значення, відповідає вхідній комбінації 
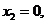
. Розглянемо мінтерм, що є добутком 
. Підставляючи в нього значення 
для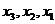 
, одержимо логічну 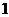. Для всіх інших семи комбінацій кон’юнкцій вони рівні логічному . Отже, мінтерм можна використовувати для опису першого рядка. Аналогічно розмірковуючи, знаходимо мінтерми для 3-го, 6-го та 8-го рядків таблиці істинності. Об’єднуючи одержані результати, одержуємо логічну функцію
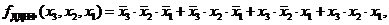
що точно описує таблицю істинності. Одержаний вираз називається логічною функцією в ДДНФ. Він визначається як сума мінтермів.
ДКНФ також може бути одержана з таблиці істинності. Звернемось знову до табл. 2.2. Таблиця визначає логічну функцію 
. Таблиця істинності для інверсної функції 
одержується інверсією значень функції . Результат представлений в табл. 2.3.
|
|
|
Табл. 2.3
|
|
| 
| 
|
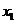
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Користуючись раніше розглянутим способом, можна записати ДДНФ для інверсної функції в наступному вигляді:
.
Якщо тепер виконати заперечення над правою та лівою частинами цієї рівності та скористатись теоремою Де Моргана, одержимо:
.
Функціонально повні системи функцій переключення булевої алгебри. Функціонально повною системою або базисом функції переключення називають системи логічних функцій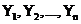 
з допомогою яких може бути представлена будь-яка функція переключення. Функціонально повними системами є базиси: І, АБО, НЕ (базис 1); І, НЕ (базис 2); АБО, НЕ (базис 3); І-НЕ (базис 4); АБО-НЕ (базис 5) та І-АБО-НЕ (базис 6).
Базис І, АБО, НЕ вважається основним, так як будь-яка складна функція переключення може бути записана у вигляді ДДНФ або ДКНФ. Базиси можуть бути надлишковими та мінімальними. Базис І, АБО, НЕ є надлишковою системою, так як можливе виключення з нього деяких функцій. Наприклад, використовуючи закони де Моргана, можна виключити або функцію І замінивши її на АБО або НЕ, або АБО, замінивши її на І та НЕ. Базиси І, НЕ та АБО, НЕ називаються нормальними базисами. Зв’язуючою ланкою між реальним елементом та його функцією переключення є полярність логіки. Розрізняють додатну (позитивну) та від’ємну (негативну) логіки. При додатній логіці в якості логічної одиниці приймають високий рівень сигналу (логічна “1”), при від’ємній – низький рівень сигналу (логічний “0”). В залежності від типу вибраної логіки одні і ті ж логічні елементи можуть реалізувати різні функції переключення.
|
|
|
Мінімізація логічної функції. Мінімальною формою представлення логічної функції називають таку форму, яка не допускає більше ніяких спрощень. При мінімізації виходять з вимоги мінімальної кількості логічних елементів, реалізованих у вигляді мікросхем. Для мінімізації логічних функцій використовуються різні методи: послідовного виключення змінних з допомогою законів та тотожностей алгебри логіки, мінімізованих карт Карно.
Метод послідовного виключення змінних з допомогою законів та тотожностей булевої алгебри є найбільш простим методом мінімізації. Будь-яке спрощення логічної функції відбувається при винесенні за дужки загальних множників. Виключення будь-якої змінної з даного мінтерму відбудеться при додаванні до нього мінтерму, що відрізняється лише значенням цієї змінної. Такий процес підбору пари мінтермів, що супроводжується пониженням рангу змінних, називається склеюванням мінтермів. Як приклад, мінімізуємо функцію переключення 
методом послідовного наближення. Для даної функції переключення, групуючи мінтерми, отримаємо:
.
Групуючи мінтерми різними способами, можна отримати різні спрощені форми заданої функції, але при цьому не можна бути впевненим, що одна з отриманих форм є мінімальною.
Метод мінімізуючих карт Карно знаходить широке використання при мінімізації логічних функцій. Карти Карно - графічне представлення всіх мінтермів ( ) для даного числа змінних . Кожний мінтерм зображується у вигляді клітинки, розміщеної так, що мінтерми, що знаходяться в сусідніх клітинках, відрізняються тільки однією змінною. На рис. 2.1. представлено зображення карт Карно для функції двох, трьох та чотирьох змінних.
| 
| 
| 
| |||||||||||
| ||||||||||||||
| 
|
|
|
|
| 
| ||||||||
| 
| 
| ||||||||||||
|
| 
|
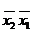
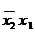
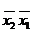
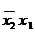
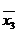
а) б) в)
Рис. 2.1. Зображення карт Карно для двох (а), трьох (б) та чотирьох (в) змінних.
Основа їх мінімізації з допомогою карт Карно полягає в наступному: два мінтерми, що знаходяться в сусідніх клітинках карти, можуть бути замінені кон’юнкцією, яка містить на одну змінну менше. Якщо сусідніми є дві пари мінтермів, то така група з чотирьох мінтермів може бути замінена кон’юнкцією, яка містить на дві змінні менше. В загальному випадку наявність мінтермів в сусідніх клітинках дозволяє виключити змінних. При мінімізації необхідно пам’ятати, що сусідніми клітинками є не тільки клітинки розміщені по горизонталі або вертикалі, але і клітинки на протилежних границях карт Карно. Клітинки можуть об’єднуватися по дві, чотири і т.д. Одна і та ж клітинка карти Карно може входити в декілька груп. Картами Карно можна користуватися для мінімізації логічної функції, заданої як в ДДНФ, так і в ДКНФ.
Розглянемо мінімізацію з допомогою карти Карно мажоритарного елемента на три входи. Мажоритарним елементом називають логічний елемент, що працює по принципу більшості, який полягає в тому, що якщо більшість вхідних сигналів рівна 1 або 0, то і вхідний сигнал буде відповідно рівний 1 або 0. Кількість входів мажоритарного елементу може бути рівна будь-якому непарному числу. На практиці найчастіше використовуються елементи з кількістю входів 3 і 5.
Робота мажоритарного елементу на три входи описується логічною функцією 
, що визначається таблицею істинності (табл. 2. 4).
Табл. 2.4.
|
|
|
|
|
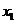
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
ДДНФ даної функції мажоритарності запишеться у вигляді:
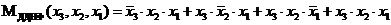. (2.1)
Виконавши мінімізацію цього виразу з допомогою карт Карно, отримаємо:
. (2.2)
Для цієї функції вводиться спеціальне позначення, яке скорочує запис логічної функції (3.13):
. (2.3)
Такий запис означає, що для отримання з неї початкової МДНФ необхідно виконати по кон’юнкції другого порядку над кожними змінними та об’єднати їх знаком диз’юнкції. На рис. 2.2 представлена схема мажоритарного елементу на три входи та його умовне графічне позначення.
а) б)
Рис. 2.2. а) схема мажоритарного елементу на три входи;
б) умовне позначення мажоритарного елементу.
Розглянемо приклад синтезу комбінаційної логічної схеми, що реалізує функцію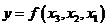 
в базисах І-НЕ та АБО-НЕ. Функція задана таблицею істинності (табл. 2.5). Для кожної схеми приведемо часові діаграми роботи.
Табл. 2.5
| № п/п |
|
|
| 
|
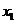
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 1 |
| 6 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 1 | 0 |
Запишемо аналітичний вираз для логічної функції, представленої в таблиці істинності:
.
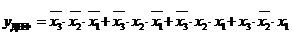З допомогою карт Карно мінімізуємо отриману логічну функцію.
а) б)
Рис. 2.3 Карта Карно для логічної функції 
:
а) мінімізація макстермів; б) мінімізація мінтермів.
. (2.4)
В результаті склеювання мінтермів в карті Карно, для яких логічна функція рівна 0, отримаємо вираз для логічної функції в мінімальній КНФ:
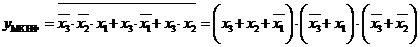. (2.5)
Представимо функції 
і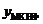 
в базисі І-НЕ:
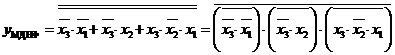. (2.6)
. (2.7)
Запишемо функції і 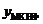в базисі АБО-НЕ:
. (2.8)
. (2.9)
На рис. 2.4. зображена схема, що реалізує логічну функцію з допомогою логічних елементів mI-HE.
Рис. 2.4. Логічна схема, що реалізує логічну функцію
з допомогою логічних елементів mI-HE
На рис. 2.5 зображена схема, що реалізує логічну функцію 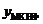з допомогою логічних елементів mАБО-НЕ.
Рис. 2.5. Схема, що реалізує логічну функцію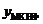
з допомогою логічних елементів mАБО-HE
Часові діаграми роботи логічної схеми (рис. 2.4) представлені на рис. 2.6.
Рис. 2.6. Часові діаграми роботи логічної схеми, зображеної на рис. 2.4.
Синтез та моделювання роботи двійково-десяткового суматора
Завдання побудови однорозрядного двійково-десяткового суматора може вирішуватися так само, як і завдання побудови однорозрядного двійкового суматора. У разі двійково-десяткового суматора необхідно буде реалізувати п'ять функцій від дев'яти двозначних змінних - чотири змінні для кожної десяткової цифри і одна змінна – перенос з молодшого розряду. При цьому вихідні функції будуть визначені лише на 200 наборах з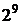 
= 512. Можна було б записати ДДНФ цих функцій і мінімізувати їх відомими формальними методами. Проте ДДНФ в цьому випадку містили б десятки диз'юнктивних членів, що значно утрудняє мінімізацію. Крім того, внаслідок великого числа невизначених значень функції важко вирішити питання про їх раціональне довизначення.
Тому двійково-десяткові суматори будують в два етапи. На першому етапі додають двійкові коди десяткових цифр по правилу двійкової арифметики. На другому етапі проводять корекцію результатів шляхом збільшення або віднімання деякої поправки, величина якої пов'язана з величиною некоректованого результату, отриманого на першому етапі. Розглянемо три приклади проектування однорозрядного двійково-десяткового суматора, зважаючи на дві обставини: перше – ДДК суми і ДДК доданків повинен бути одним і тим же; друге - двійково-десятковий суматор повинен формувати десятковий перенос, тобто перенос з вагою 10.
Дата добавления: 2018-04-04; просмотров: 293; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!