Классификация квадратичных форм

Квадратичные формы

Определение. Квадратичной формой от n неизвестных называется многочлен от n переменных второй степени, не содержащий членов первой степени и свободного члена

причем " ( ).

Замечание. С учетом условия " ( ) квадратичную форму обычно записывают в виде:

Из коэффициентов 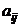можно составить квадратную матрицу n-го порядка

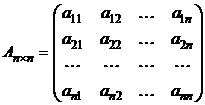которая называется матрицей квадратичной формы f, а ее ранг r называется рангом квадратичной формы f.

Если , т.е. матрица A невырождена ( ), то и квадратичная форма f называется невырожденной.

Из условия " ( ) следует, что , т.е. матрица A – симметрическая.

Обратно, для любой симметрической матрицы A n-го порядка можно указать вполне определенную квадратичную форму f от n неизвестных, имеющую элементы матрицы A своими коэффициентами.

Пример 1. Составить матрицу A квадратичной формы от трех неизвестных

Решение. Матрица этой квадратичной формы имеет вид:

Пример 2. Указать квадратичную форму f, соответствующую симметрической матрице

Является ли указанная квадратичная форма невырожденной?

Решение. Порядок матрицы A равен трем, поэтому квадратичная форма f будет зависеть от трех неизвестных. Тогда

Вычислим определитель: . Поскольку , то квадратичная форма f невырождена.

Если 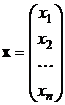– матрица столбец из n неизвестных, то . Тогда для любой квадратичной формы f (с матрицей A), очевидно, возможна следующая матричная запись:

Определение. Линейным преобразованием неизвестных называется такой переход от системы n неизвестных , , …, к системе n неизвестных , , …, , 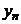при котором старые неизвестные линейно выражаются через новые (с некоторыми числовыми коэффициентами):

Линейное преобразование неизвестных удобно записывать в матричном виде:

где , , .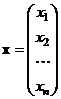

Очевидно, что любое линейное преобразование неизвестных однозначно определяется своей матрицей Q.

Линейное преобразование неизвестных является невырожденным в том и только в том случае, когда его матрица Q – невырождена. Если же матрица Q является при этом ортогональной (т.е. ), то линейное преобразование неизвестных называется ортогональным.

Вопрос. Что произойдет с квадратичной формой f, если , , …, будут подвергнуты линейному преобразованию ?

Ответ. Квадратичная форма с матрицей A после выполнения линейного преобразования неизвестных (с матрицей Q) превращается в квадратичную форму от новых неизвестных , , …, , 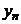с матрицей . Действительно, пусть , тогда . Отсюда

Покажем теперь, что матрица B – симметрическая, т.е. . Действительно,

т.к. матрица A – симметрическая по условию ( ).

Замечание. Очевидно, что ранг квадратичной формы не изменяется при выполнении невырожденного линейного преобразования неизвестных.

Довольно часто на практике требуется выполнять не одно линейное преобразование неизвестных, а несколько, причем последовательно.

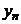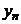Пусть переход от неизвестных , , …, к неизвестным , , …, задается матрицей ( ), а затем переход от , , …, к неизвестным , , …, задается матрицей ( ). Тогда

Таким образом, последовательное выполнение двух линейных преобразований неизвестных вновь является линейным преобразованием от , , …, к , , …, с матрицей Q, причем

Определение. Квадратичная форма имеет канонический вид, если все коэффициенты при произведениях различных неизвестных равны нулю, т.е. " ( ), и не все .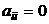

Замечание. В каноническом виде квадратичная форма записывается следующим образом: , где не все .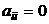

Теорема 1. Любая квадратичная форма может быть приведена к каноническому виду с помощью некоторого невырожденного линейного преобразования неизвестных. При этом число ненулевых коэффициентов в этом каноническом виде (т.е. коэффициентов при квадратах неизвестных) не зависит от этого преобразования и непременно равно рангу этой квадратичной формы. (Без доказательства.)

Пример. Дана квадратичная форма . Привести эту форму к каноническому виду с помощью невырожденного линейного преобразования неизвестных.

Решение. Выделим вначале полный квадрат по переменной , получим:

Далее, выделим полные квадраты по переменным и :

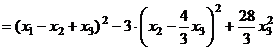Положим

Тогда квадратичная форма f примет канонический вид:

Покажем, что линейное преобразование неизвестных, приводящее квадратичную форму f к каноническому виду, является невырожденным. Найдем матрицу Q этого преобразования. Действительно, в матричном виде замена переменных

приводящая квадратичную форму f к каноническому виду , выглядит следующим образом:

Матрица , очевидно, невырождена. Поэтому и матрица линейного преобразования неизвестных ( ) – также невырождена. Значит, и само линейное преобразование является невырожденным. Найдем явный вид этого линейного преобразования неизвестных. Поскольку , то

Отметим также, что ранг исходной квадратичной формы f равен 3, т.к. число ненулевых коэффициентов в каноническом виде равно 3.

Замечание. Описанный в этом примере метод приведения квадратичной формы к каноническому виду (с помощью последовательного выделения полных квадратов) носит название метода Лагранжа.

Следует отметить, что любая квадратичная форма может быть приведена к каноническому виду с помощью ортогонального преобразования, причем коэффициенты при квадратах неизвестных будут совпадать с собственными значениями матрицы A квадратичной формы, а столбцы матрицы Q преобразования неизвестных будут состоять из соответствующих взаимно-ортогональных ортов собственных векторов матрицы A квадратичной формы.

Теорема 2 (закон инерции). Если квадратичная форма приводится к каноническому виду двумя различными невырожденными преобразованиями, то число членов с положительными коэффициентами, так же как и число членов с отрицательными коэффициентами, в обоих случаях будет одно и то же. (Без доказательства.)

Пример. Привести квадратичную форму к каноническому виду двумя способами: с помощью ортогонального преобразования (записать явный вид этого преобразования) и методом Лагранжа. Проверить выполнение закона инерции.

Решение. 1-й способ. Матрица квадратичной формы имеет вид: . Собственные значения:

Û Û

Тогда орты собственных векторов:

(для ); (для ).

Отметим, что и (в силу того, что матрица A – симметрическая, собственные числа различны) взаимно-ортогональны. Впрочем, условие ортогональности и можно проверить и непосредственно, т.к. скалярное произведение . Отсюда, матрица Q ортогонального преобразования имеет вид:

Тогда явный вид этого ортогонального преобразования следующий:

С помощью этого преобразования квадратичная форма f примет вид:

2-й способ. Выделим полные квадраты по переменным и :

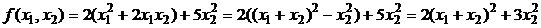Положим , 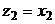. Тогда квадратичная форма f примет вид: .

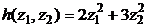Закон инерции, очевидно, выполняется.

Классификация квадратичных форм

Определение. Квадратичная форма называется положительно определенной, если на любых наборах значений неизвестных , , …, , (т.е. кроме набора неизвестных, когда ).

Определение. Квадратичная форма называется положительно полуопределенной, если на любых наборах значений неизвестных , , …, .

Определение. Квадратичная форма называется отрицательно определенной, если на любых наборах значений неизвестных , , …, , (т.е. кроме набора неизвестных, когда ).

Определение. Квадратичная форма называется отрицательно полуопределенной, если на любых наборах значений неизвестных , , …, .

Определение. Квадратичная форма называется неопределенной, если существуют наборы значений неизвестных , , …, , на которых и .

Замечание. Ясно, что положительно определенная квадратичная форма после приведения к каноническому виду будет иметь только положительные коэффициенты при квадратах всех n неизвестных. Для положительно полуопределенной формы (после приведения к каноническому виду) – неотрицательные коэффициенты (некоторые могут быть равны нулю).

Задание 1. Сформулируйте самостоятельно аналогичные утверждения для отрицательно определенных и полуопределенных квадратичных форм.

Задание 2. Сформулируйте самостоятельно аналогичное утверждение для неопределенных квадратичных форм.

Теорема 3 (критерий Сильвестра). Квадратичная форма является положительно определенной тогда и только тогда, когда все угловые миноры матрицы квадратичной формы положительны. То есть , , , 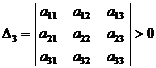… , . (Без доказательства.)

Следствие. Квадратичная форма является отрицательно определенной тогда и только тогда, когда знаки угловых миноров матрицы A квадратичной формы чередуются, начиная со знака «минус», т.е. , , …

Действительно, " , , …, таких, что Û Û Û матрица имеет все положительные угловые миноры: , , , … , .

Таким образом, , , , … ■

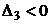Пример. Является ли положительно определенной квадратичная форма

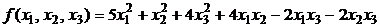Решение. Матрица квадратичной формы имеет вид: . Тогда 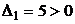, , . Значит, по критерию Сильвестра, квадратичная форма 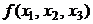является положительно определенной.

Дата добавления: 2018-02-28; просмотров: 2810; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!