Волна T. Волновое сопротивление коаксиальной линии
ЭЛЕКТРОМАГНИТТІ ЖОЛАҚТАР ЖӘНЕ ТОЛҚЫНДАР
2-ші бөлім
6М071900 – Радиотехника, электроника және телекоммуникация мамандығы бойынша оқитын магистранттарға арналған
оқу құралы
КІРІСПЕ
1. ГАРМОНИКАЛЫҚ ЖОЛАҚТЫҢ ЭЛЕКТРОДИНАМИКАЛЫҚ ӘЛЕУЕТІ
1.1. Гельмгольцаның теңдеуі…………………………………...……………….9
1.2. Гельмгольцаның әр түрлі теңдеу шешімдері............ ................................10
2. ТЕГІС ЭЛЕКТРОМАГНИТТІ ТОЛҚЫНДАР ..................................................12
2.1. Ортақ ақпараттар .........................................................................................12
2.2. Электромагнитті тегіс толқындар бірдей изотропты ортада шығынсыз мәнге ие .....................................................................................................................12
2.3. Тегіс толқындар және өткізгіштігі нөлден жоғары бірдей изотропты ортада..........................................................................................................................15
2.4. Шынайы диэлектрдағы толқындардың таралуы......................................19
2.5. Шынайы металлдағы толқындардың таралуы..........................................20
2.6.Толқындардың поляризациялануы..............................................................21
3.ТОЛҚЫНДАРДЫҢ ШЕКАРАДАҒЫ ЕКІ ОРТАДАН КӨРІНІСІ ...................24
3.1. Тегіс толқындардың туынды бағдарлауы .................................................24
3.2. Тегіс толқындардың шекарадағы екі диэлектрикке құлауы....................25
|
|
|
3.3. Бірқалыпты поляризация.............................................................................26
3.4. Параллельді поляризация ...........................................................................29
3.5.Толқындардың екінші ортаға өтудегі толық шарты. Брюстер..................31
3.6. Шекарадағы ортадан толық шағылыс. Екі диэлектрикалық орта...........32
3.7.Толық іштегі шағылыстын туу шарты .......................................................33
4 . АТТАМАЛЫ ӘСЕР..............................................................................................38
4.1. Аттамалы әсердің пайда болуы...................................................................38
4.2. Өткізгіштердегі энергияның жоғалуы........................................................39
Эквивалентті аттамалы ток..........................................................................41
5.ЭЛЕКТРОМАГНИТТІ ТОЛҚЫНДАРДЫҢ СӘУЛЕЛЕНУІ.............................42
5.1.Ортақ түсініктер............................................................................................42
5.2.Жолақтың сәулеленуі ЭЭИ...........................................................................42
5.3.Бағытталған диаграмма.................................................................................45
6.БАҒЫТТАЛҒАН ЖӘНЕ АТТАМАЛЫ ТОЛҚЫНДАР.....................................46
6.1.Толық ішкі шағылыс.....................................................................................46
6.2.Бірқалыпты поляризациядағы бірінші ортадағы жолақ............................47
|
|
|
6.3.Бірқалыпты поляризациядағы екінші ортадағы жолақ ............................48
7. ЖОЛАҚТЫҢ СУРЕТІ, ТЕГІС ТОЛҚЫНДА ПАЙДА БОЛҒАН МІНСІЗ МЕТАЛЛДЫҢ ҚҰЛАУЫ.........................................................................................48
7.1.Құлау жолағында Е векторы. Электр типтес толқындар...........................48
7.2.Е векторы құлай тегісіне перпендикуляр.Магнит типтес толқындар......52
Екітегісті волновод........................................................................................52
8. БАҒЫТТАЛҒАН СИСТЕМАЛАР ЖӘНЕ БАҒЫТТАЛҒАН ЭЛЕКТРМАГНИТТІ ТОЛҚЫНДАР………………………………….………......55
8.1. Бағытталған толқындар……………………………………………….........55
8.2. Бағытталған толқындардың бағыты............................................................55
8.3.Бойлық және көлденен жолақтардың бірдей бағытталған системадағы байланысы …………………….......................................……………….....……55
8.4. Критикалық жиілік. Критикалық толқынның ұзындығы........................57
9. КӨЛДЕНЕН ЭЛЕКТРОМАГНИТТІ ТОЛҚЫНДАР..........................................58
9.1.(Еz =0 , Нz =0) .Критикалық толқынның ұзындығы..................................58
9.2. Тұрақты таратылу. Толқынның фазалық жылдамдығы...........................59
|
|
|
9.3. Мінездемелік қарсылық..............................................................................60
10.ЭЛЕКТРЛІ ТОЛҚЫНДАР..................................................................................61
10.1.Жолақтардың өзаралық байланысы (  и
и 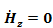 ).............................61
).............................61
10.2. Мінездемедік қарсылық.............................................................................61
10.3. Фазалық жылдамдық. Дисперсия……………...............…......................62
11.БАҒЫТТАЛҒАН СИСТЕМА..............................................................................62
11.1. Тікбұрышты толқынжүргізгіш.Электорлы толқындар ( 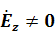 және
және 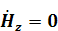 )..................................................................................................................62
)..................................................................................................................62
11.2. Магнитті толқындар ( 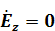 және
және 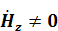 ).............................................65
).............................................65
11.3. Толқын Н10 ...................................................................................................66
11.4. Домалақ толқынжүргізгіш........................................................................68
11.5. Электрлі толқындар..................................................................................68
11.6. Магнитті толқындар ( 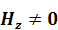 ,
,  ). ................................................ 71
). ................................................ 71
11.7 Коаксиалды толқынжүргізгіш.................................................................72
11.8 Толқын T. Коаксиалды сызықтағы толқынжүргіштік кедергі..............72
11.9 Электрлі және магнитті толқындар..........................................................73
|
|
|
11.10 Коаксиаолды сызықтағы диаграммалардың типтері...........................75
12. ДІРІЛДЕГІШ ЖҮЙЕЛЕР СВЧ.КӨЛЕМДІ РЕЗОНАТОРЛАР................…...75
12.1. Электромагнитті дірілдегіш жүйесінің эволюциясы………………......75
12.2. Тікбұрышты толқынжүргіштегі көлемді резонатордың бөлшегі .........78
12.3. Тербеліс түрлері H10p . Жолақтың структурасы H101………..……..….79
12.4.Тікбұрышты резонатордағы тербелістердің ортақ есебі, толқын түрлерінің классификациясы..............................................................................80
12.5. Тербеліс түрлерінің классификациясы………........................……...…..82
12.6.Цилиндрлық көлемді резонатор.................................................................82
12.7.Көлемді резонаторлардың қозу әдістері....................................................83
12.8.Көлемді резонаторлардың беріктігі...........................................................85
12.9. Көлемді резонаторлардың басқа түрлері..........…..…………………....86
13. ЭЛЕКТРОАГНИТТІ ТОЛҚЫНДАРДЫҢ АНИЗОТРОПИЯЛЫҚ ОРТАДА ТАРАЛУЫ………………………………..........................…….....………………...87
13.1. Ортақ ақпараттар.….…………………………………….....…………….87
13.2. Магниттелген ферриториялық ортада сызықты толқындар. ................87
13.3. Гиромагнитті ортадағы толқындардың доға тәрізді поляризациясы...89
13.4. Фарадей әсері……………………………………………………….....…90
14. АТТАМАЛЫ ТОЛҚЫННЫҢ ӨТПЕЛІ СЫЗЫҚТАРЫ……………...….......93
14.1. Өтпелі сызықтың бірсымдығы………………………………………......93
 |
14.2.Диэлтрикалық толқынөткізгіштік..............................………………........94
14.3. Талшықтық жарықжетекшіс..................…………………………………96
Әдебиет ...................................................................................................................102
 НЕГІЗГІ БЕЛГІЛЕР
НЕГІЗГІ БЕЛГІЛЕР
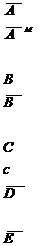
-векторлы потенциал, Вб/м
-векторлы магнитті потен-
циал, Кл/м
-реактивті өткізгіштік,
Сим
- магнитті вектордың индукциясы
Вб/м2
-сыймдылық ,Ф
-вакуумдағы жарықтың жылдамдығы,
м/сек
-электролы вектордың жылжуы
Кл/м2
-электоры жолақтың вектор кернеуі
, В/м
е -электроқозғалушы күш
(лездік мағына),В
е -негізгі натуралды логарифмдер
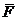 -вектор күші, Н
-вектор күші, Н
f -жиілік ,Гц
G -өткізгіштік , Сим
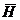 - электоры жолақтың вектор кернеуі
- электоры жолақтың вектор кернеуі
, А/м
I -электорлы ток(лездік мағына), А
Iм - магнитті ток (лездік мағына), В
Iсм -жылжу тогы (лездік мағына), А
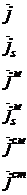 Iст -жақын ток (лездік мағына), А
Iст -жақын ток (лездік мағына), А
i -жалған бірлік (i2=-1)
-токтың нығыздалған векторы
 өткізгіштігі, А/м2
өткізгіштігі, А/м2
-аттамалы вектордың тығыздығы
, А/м
-магнитті токтың вектор тығыздығы
, В/м2
-токтың, магниттің токтың тығызды,ы
В/м
-жылжу тогының вектор тығыздығы
-шеткі токтың вектор тығыздығы
,А/м2
Кбв -жылжымалы токтың векторы
kм -магнитті қабылдауыштың ортасы
Kсв - автивті толқынның коэффициенті
kэ -диюлекторлы қабылдауыштың ортасы
L -индуктивтілік, Гн
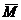 -магниттелген вектор А/м
-магниттелген вектор А/м
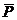 -поляризованный ортаның векторы
-поляризованный ортаның векторы
К/м2
PП -жоғалу қуаты (лездік мағына),Вт
Pст -басқа бастаулардың қуаты
(лездік мағына),Вт
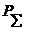 -сәулелену қуаты (лездік мағына),В т
-сәулелену қуаты (лездік мағына),В т
P -комплексты қуат, Вт
Pa -басқа активті қуаттар, Вт
Pr -автивті емес басқа қуаттар, Вт
p -шағылысу коэффициенттің комплексы
(өткізу жолағында)
p -дирольдік кез (электорлы дипольдың моменті) К٠ м
pм -магниті дипольдің моменті, Вб۰ м
Q -беріктілік
Q,q –электорлы заряд ,К
R -активті кедергінің электорлы цепі, Ом
Rs -аттамалы кедергінің өткізгіштік активті бөлігі, Ом
 -с»улелені кедергісі, Ом
-с»улелені кедергісі, Ом
 R и R -көріну коэффициенті
R и R -көріну коэффициенті
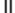
S -аттманың көлемі,м2
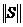 -жайылудың толқындық матрицасы
-жайылудың толқындық матрицасы
T -тербеліс периоды, сек
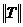 -өткізу толқынының матрицасы
-өткізу толқынының матрицасы
u -скалярлық потенциал (лездік мағына) , В
u -электростатикалық потенциал, В
uм -магниттістатикалық потенциал, А
V -көлем м3
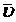 -векторжылдамдығы, м/сек
-векторжылдамдығы, м/сек
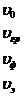 -жарықтың ортадағы жылдамдығы, м/сек
-жарықтың ортадағы жылдамдығы, м/сек
-топтық жылдамдық, м/сек
-фазалық жылдамдық,м/сек
-энергия тарату жылдамдығы, м/сек
 W -электромагнитті жолақтың энергиясы, Дж
W -электромагнитті жолақтың энергиясы, Дж
Wм –магнитті жолақтың энергиясы, Дж
Wэ -электорлы жолақтың энергиясы 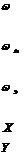 Дж
Дж
-электромагнитті жолақтың энергия тығыздығы
, Дж/м3
-магнитті жолақтың энергия тығыздығы
, Дж/м3
-электорлы жолақтың энергия тығыздығы
, Дж/м3
-электорлы цептағы активті емес кедергі
, Ом
-комплексты өткізгіштік,
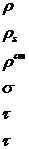 Сим
Сим
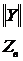 -өткізгіштік матрицасы
-өткізгіштік матрицасы
-сызықтық кедергінің толқындығы
, Ом
Zc -мінездемелік кедергі, волновое сопративление
среды, Ом
Zs -өткізгіштің аттамалы кедергісі, Ом
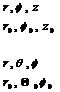
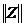 -кедергі матрицасы
-кедергі матрицасы
y,x,z –декартовы координаты
x0,y0,z0 – декартты жүйеніңбағытталған координаты
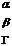 -әлсіреу коэффициенті 1/м
-әлсіреу коэффициенті 1/м
-коэффициент фазасы , 1/м
-шоғырлану
Г -Герцтың векторы, В· м

-өткізу тереңдігі, 1/м
-диэлектрлік жоғалудың тереңдігі
-салыстырмалы диэлектрлік өткізгіштік
-электрлігі тұрақты, Ф/м
-абсолютті диэлектрлі тұрақтылығы
, Ф/м
-комплексті диэлекторлы кіру
, Ф/м
-диэлекторлы өткізгіштің тендоры
, Ф/м
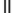 x и x - бірқалыпты және параллельді толқынның құлау кезінде сәкесінше коэффициенттің өткізу жолағы
x и x - бірқалыпты және параллельді толқынның құлау кезінде сәкесінше коэффициенттің өткізу жолағы
-бағытталған жүйедегі толқынның ұзындығы, м
-толқын ұзындығы, м
-толқынның критикалық ұзындығы,м
- салыстырмалы магнитті өткізгіш
-магнитті тұрақтылығы, Гн/м
-абсолютті магнитті өткізу, Гн/м
-магнитті өткізудің тензоры,
Гн/м
П - Пойнтинга векторы, Вт/м2
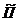 - Пойптинга векторының комплексты түрі
- Пойптинга векторының комплексты түрі
- зарядтың көлемді тығыздығы
- аттамалы зарядтың нығыздығы
- нығыздалған зарядтың көлемі
-үлесті өткізгіштік,Сим/м
-электорлы зарядтың сызықты нығыздығы, Кл/м
- релакция уақыты, сек
Ф - магнитті тасқын, Вб
-цилиндрлік координаттар
-цилиндрлік жүйенің сәйкестендірілген координаты
-шеңбердің координаты
-шеңбер жүйесінің сәйкесінше бағытталған коорлинаты
КІРІСПЕ
Қазіргі телекоммуникацияда радиотехника жүйесінің бөлшегі күннен күнге көбеюде. Бұл ретте жұмыс диапазонында пайдаланушы тербелістердің спектрдің жоғары жиілігіне жылжиды. Мысалы, диапазонның мүмкіндіктерін тауысуы 4…6 ГГц, спутниктік телевидение келесі интервалда алған өлшемі 11…14 ГГц, телевещанияның үшінші тұқымы космостың ретрянсляторы 20…30 ГГц диапазонында игеруге дайындалып жатыр.Сигналдың жиілігі ұлғайған уақытта каналдың саны көбейе бастайды, яғни колданбалы диапазонның сыйымдылғы ұлғайады. Оптикалық диапазонның мүмкіндіктері, жиілігі 3∙1012 Гц жоғары, төтенше жоғары. Тап сол себептен қазіргі телекоммуникацияда талшықты оптикалық байланыс алдыңғы орынды алады. ТОБЖ-ның негізі бөлшегі кварцтық жіп, қабылдаушы және өткізуші стационар құрылғыларды байланыстырады. Бірақ жылжымалы ТОБЖ нысандары байланыстың басты түрі болып жұмыс жасай алмайды – жылжымалы корреспондент үшін бос жайылатын радиотолқындар үшін қолдану өте оңтайлы. Жылжымалы нысандардың ұялы байланысы кең түрде қолданылуда, мәселен, жиілік диапазоны 900 МГц және 1800 МГц.
Қазіргі телекоммуникациядағы жүйенің келтірілген мысалдары көрсетеді, жиіліктің жоғары спектрін қолдану дұрыс бағыт болып табылады.Өте жоғары жиілікті техниканың теориялық базасы (сонымен қатар оптикалық) байланыс Максвелл теңдеуіне негізделген және оны алгебрадағы вектор элементінде сонымен қатар векторлық анализда қолданады. АЖЖ(аса жоғары жиілік) құрылғысында толқынды көріністерді зерттеу немесе бос жазықтықта және өткізу сызығында квантты физикалық дәрежеде сұрақтарды қарастыру міндет емес, жазықтықта оларды үздіксіз көру де жеткілікті.
Толқынды процессты қарастыру кезінде, жайылу толқыны диэлекторда және өткізгіште әр түрлі және олардың параметрлары бір бірінен айырмашылығы өте айқын. ЭМВ ортадағы шекара бөлшегіне құлағанда, оптика заңына бағынады және өзінің ерекшеліктеріне ие.
Бағытталған толқындардың толық толқын және олардың ерекшеліктерін қарастырамыз .Сонымен қатар, көлемді резонаторлар жайлы сұрақтар қозғалды. Талшықты оптикалық сызық байланысының қолдану түсініктері көрсетілді.
1. ГАРМОНИКАЛЫҚ ЖАЗЫҚТЫҚТЫҢ ЭЛЕКТРОДИНАМИКАЛЫҚ ПОТЕНЦИАЛДАРЫ
1.1. Гельмгольца теңдеуі
Электродинамиканың барлық есептері 2 түрге бөлінеді:
· тура есептер, электромагнитті жазықтықта берілген есептер бойынша сәкесінше қажетті бөлшекті табуға болады;
· кері есептер, берілген электромагнитті есептер бойынша, сәйкесінше керекті анықтамаларды алуға болады.
Бұл бөлімде тура және кері электродинамиканың есептерді шығару әдістерін қарастырмыз.
Есептердің көптігі соншалық жолақтағы векторды есептеп шығару өте қиын. Комплексты амплитуда әдісін пайдаланып гармоникалық жолақ үшін есепті шығаруға болады. Электродинамикадағы кез келген есепті шығару үшін Максвелл теңдеуін қолданамыз. Максвелл теңдеуін дифференциалды теңдеу формасына түрлендіруді теңдеу формасына түрлендіруді іске асырады. Гармоникалық электромагнитті процессті қарастырамыз. Максвелл теңдеуін комплексті амплитуда үшін жазамыз.
 . (1.1)
. (1.1)
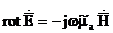 . (1.2)
. (1.2)
Оң жақ бөліктен сол жақ бөлікке роторды аламыз. (1.1).
Сонда
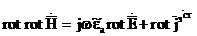 . (1.3)
. (1.3)
Белгілі теңдеуді қолданамыз

Максвеллның төртінші теңдеуінен 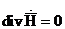 , яғни
, яғни
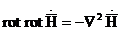 . (1.4)
. (1.4)
Орнына қоямыз (1.4) және (1.2) әрекеттесуі (1.3) одан шығатыны 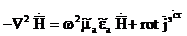 немесе
немесе
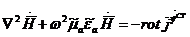 , (1.5)
, (1.5)
сонда
к=  .
.
Сонымен жоғарыда келтірілген түрлендіруде біз бірдей емес дифференциалды теңдеуді алдық, математикалық физикадағы атауы Гельмгольцтың әр түрлі теңдеуі.Бұл теңдеу толқынды процестерді көрсетеді.
1.2. Гельгольцтың түрлі теңдеуін шешу.
Гельмголцтың әртүрлі теңдеуін шешу үшін 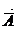 векторлы функциясын кіргізеді оны вектордың электрлі потенциалы деп атайды.
векторлы функциясын кіргізеді оны вектордың электрлі потенциалы деп атайды.
Келесідей векторлы әдістер бар
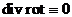 и
и 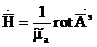 (1.6)
(1.6)
Гельмгольцтың әртүрлі теңдеуін аламыз
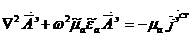 . (1.7)
. (1.7)
(1.6) теңдеуін (1.7) теңдеуіне қоямыз да, мына теңдеуді аламыз: 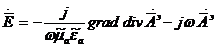 . (1.8)
. (1.8)
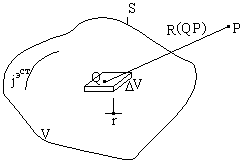
1.1. Суретін қарастырамыз. Жолақтың мінездемелік Р нүктесіндегі көлем сыртындағы V-ны анықтау қажет,сонымен көлем ішіндегі кез келген нүктеден Р нүктенің көлемінен үлкендеу қашықтықтан алу керек.
|
|
Рис 1.1 Жолақтың мінездемелік қасиетін анықтау
Көлемнің ішінен V нүктесін Q және оның айналасында қарапайым көлем тұрғызамыз DV. R — нүкте арасындағы қашықтық Q және Р.Біз 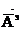 жолақтың қарқының іздейміз, Р нүктесінен басқа да токтар әсер етуде.Бұл қарқын
жолақтың қарқының іздейміз, Р нүктесінен басқа да токтар әсер етуде.Бұл қарқын 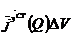 .
. 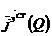 — пропорционал кейбір орташа мән токтың көлем нығыздығына байланысты.
— пропорционал кейбір орташа мән токтың көлем нығыздығына байланысты. 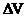 көлемнің мөлшері R қашықтығынан әлдеқайда алысырақ, сондықтан
көлемнің мөлшері R қашықтығынан әлдеқайда алысырақ, сондықтан 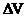 басқа да токтармен өтіп жатқан, оны нүктелік негіз ретінде қарауға болады. Симмерия күшінде жолақтың қарқының бірдей изотропты жазықтықта нүктелік негізін аттамалы фазасы теңбе тең, яғни сфера түріне ие болады.
басқа да токтармен өтіп жатқан, оны нүктелік негіз ретінде қарауға болады. Симмерия күшінде жолақтың қарқының бірдей изотропты жазықтықта нүктелік негізін аттамалы фазасы теңбе тең, яғни сфера түріне ие болады.
Қарапайым әдіспен қарағанда, жолақтың амплитудасы, нүктелік негіз r ғана тәуелді.
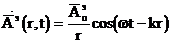 , (1.9)
, (1.9)
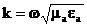 , т.е.еш жоғалусыз орта.
, т.е.еш жоғалусыз орта. 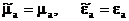 ,
,
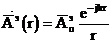 , (1.10)
, (1.10)
r — радиальды координат. Соңғы әрекеттесу сфералық толқынды суреттейді. Осы әдіспен, жазықтық осы токтармен әрекеттескендегі көлемі DV .
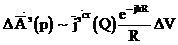 . (1.11)
. (1.11)
Максвелл теңдеуі және одан шығатын Гельмгольца теңдеуі сызықты дифференциалды теңдеуі болып табылады, сондықтан оларға суперпозиция принципі дұрысырақ болып келеді. Бұл әдісте суперпозиция әдісі: жолақ, әр түрлі көлеммен әрекеттесуі, көлемнің ішінде V болуы, суперпозиция жазықтығын елестетуге болады, басқа да бір токтардың әрекетінен, ішіндегі қарапайым көлемнің өтуімен.
Теңбе тең пайда болу үшін, пропорционалды коэффициентті анықтау керек, V қарапайым көлемнің белгілі бір санның шексіз көбеюі соңғы нәтижеде анықталуы мүмкін. Математикалық физикада Гельмгольца теңдеуінің ортақ есебін шешкенде, бұл өту
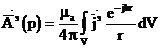 . (1.12)
. (1.12)
2 ТЕГІС ЭЛЕКТРОМАГНИТТЫҚ ТОЛҚЫНДАР
2.1 Жалпы мағлұматтар
Толқындарда үздіксіз ортада тербелгіш қозғалыстар түсіндіріледі. Толқындық процесстің математикалық сипаттамада принциптік айырмашылығы радиотехникалық тізбекте тербелгіш тоғы және кернеуінің мәні, әрбір жүйені толық сипаттау үшін схемадағы әртүрлі жерде орналасқан тоқ пен кернеудің соңғы санын білу керек. Толқындық процессті толық баяндау үшін оның қарастырылып отырған аудандағы шексіз улкен сандық нүктесінің сипаттамасын білу керек. Толқындық процесстің табиғаты аса түрлі: электромагниттік толқын, акустикалық, гравитациялық және т. б. Физиктердің айтуынша, әртүрлі толқындарды тарату кезінде айнала ақырындап кейбір физикалық процесске тартыла бастайды, нәтижесінде энергия кеңестікке тарала бастайды.
2.2. Тегіс электромагниттық толқындар жоғалтусыз біркелкі изотроптық ортада
Еркін гармоникалық тербелістер электромагниттік өрістегі жоғалтусыз біркелкі изотроптық ортада қарастырамыз. Бұл кезде Гельмгольцтің электромагниттік ортадағы векторға қатысты теңдеуі ыңғайлы
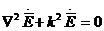 (2.1)
(2.1)
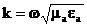 . (2.2)
. (2.2)
Векторлық теңдеуді (2.1) үш скалярлық теңдеу системасы түрінде жазуға болады:
 (2.3)
(2.3)
(2.3) теңдеудің шешімі тегіс электромагниттік толқындарда көрінеді. Тегіс электромагниттік толқындарда түсініктелуі, координаттық линияның бойлай таралуы, әрбір белгіленген уақыт моменті тегістікте тұрақты, перпендикулярлық бағытта таралуы. Толқын z осьіне бойлай таралады деп болжайық, Пойнтинг векторы
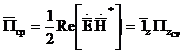 (2.4)
(2.4)
(2.4) теңдеуін байқағандай Пойнтинга векторы электромагниттік өрістің компонеттері арқылы анықталады, xoy жазықтығында орналасқан. Дәл осы жағдайда z осінің құраушылары жоқ. Сөйтіп, келесі қағидалар орындалуы қажет: өрісті анықтау кезінде тегістікте толқын таралуы өзгермеуі керек, онда
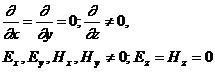 (2.5)
(2.5)
(2.5) қатынасын қолдану арқылы, (2.2) және (2.3) теңдеуін келесі түрде жазуға болады
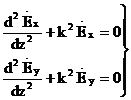 (2.6)
(2.6)
Әрбіреуін теңдеуден есептеу
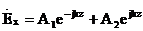 (2.7)
(2.7)
 (2.8)
(2.8)
Тұрақты интегралдау санын арттырмау үшін, 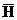 өрісіндегі компоненттерді табамыз, (2.7), (2.8) шешімдерін қолданып және Максвелл теңдеуін .
өрісіндегі компоненттерді табамыз, (2.7), (2.8) шешімдерін қолданып және Максвелл теңдеуін .
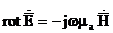 ,
,
 (2.9)
(2.9)
Бұл теңдеудің шешімі түрлендіргеннен кейін:
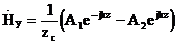 (2.10)
(2.10)
 (2.11)
(2.11)
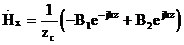 (2.12)
(2.12)
где 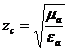 , [Ом] — ортаның сипаттамалық кедергісі, ортаның қасиетін анықтайтын.
, [Ом] — ортаның сипаттамалық кедергісі, ортаның қасиетін анықтайтын.
Формулалар (2.10), және (2.11)-(2.12) Пойнтинг векторын құрайды, z осі бойынша. Алынған есептер екі қосылған суммасын білдіреді. Әрбір қосылғыштың физикалық мәні анықтайық.
Сонымен, біз алған есептерде (2.10) бірінші қосылғыш - тегіс толқын үшін оң бағытта, екінші қосылғыш - теріс бағытта.
k толқындық санының физикалық мәнін анықтайық. k толқындық саны толқындық фазаның радианға өзгергендегі оның жолы 1 метр болғанда көрсетеді. Минимальдік қашықтығы толқындық фаза 2p-ге өзгереуін толқын ұзындығы деп атайды
 (2.13)
(2.13)
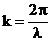 (2.14)
(2.14)
Алынған шешімдерді 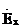 мысалында талдаймыз (2.7)-(2.11)
мысалында талдаймыз (2.7)-(2.11)
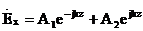 , (2.15)
, (2.15)
Бұл шешімдерде қосылғыштарды көрсетеміз, яғни толқынғв жанасатынын, z осьінде оң бағытта таралатын:
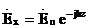 (2.16)
(2.16)
Лездік мәндеріне өтеміз:
 (2.17)
(2.17)
Келтірілген қатынаста төмендегіні қарастырамыз
- z = const кезінде тең фазаның беті өзінің тегістігін көрсетеі;
- тең амплитуданың беті тең фазаның бетімен сәйкес келеді;
- бағытталған таралуда құраушы өрісі жоқ ;
-өріскомпоненті тегіс толқында өзара- ортогональдік және толқынның таралуына перпендикуляр.
Орта біртекті, изотропты және жоғалтусыз болғандықтан,
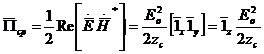 . (2.18)
. (2.18)
Энергия таралуының жылдамдығын анықтайық:
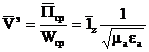 . (2.19)
. (2.19)
Фазалық жылдамдық үшін теңдеуі:
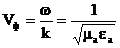 ,
,
мұндағы
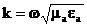 . (2.20)
. (2.20)
Онда ортаның жоғалтусыз жағдайы
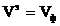 . (2.21)
. (2.21)
Толық шешімді әртүрлі комбинация үшін тегіс электромагниттік толқын бір және сол тегістік толқында әртүрлі таңдалған координаттық системаның ориентациясына қатысты.
2.3 Біртекті изотроптық ортада өткізгіштік нөлден ерекшеленетін тегіс толқын
Нөлден ерекшеленетін өткізгіштік ортада электромагниттік толқындардың энергиясы қозу және өткізгіштік тоғын қолдау үшін біртіндеп ішінара жұмсалады. Бұл кезде ортада диэлектрлік және магниттік жоғалтулар кездесуі мүмкін. Онда:
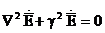 (2.22)
(2.22)
 (2.23)
(2.23)
Бұл жағдайда формула бойынша шешу алдыңғы параграфтағы мәліметтермен сәйкес келеді.
 (2.24)
(2.24)
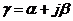 (2.25)
(2.25)
Физикалық мәнін анықтау үшін лездік берілгенге көшеміз:
 , (2.26)
, (2.26)
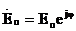 . (2.27)
. (2.27)
комплекстік тұрақты орналастыру g -дың тұрақты мәні:
b — оның негізгі бөлімі, мағынасы k-гі мәнімен бір , толқын фазасының радианда толқындық жолы 1 метр болғандағы өзгеруін көрсетеді;
a — жалған бөлімі g. Толқын амплитудасының 1 метр жолында қанша рет төмендеуін көрсетеді..
Ортадағы жоғалту соңғы өткізгіште болғанын қарастырамыз(тек Джоулевтық жоғалту):
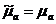 и
и 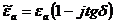 ,
,
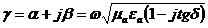 (2.28)
(2.28)
b и a үшін берілгенін алу үшін , квадратқа тұрғызамыз және келесі формуланы аламыз :
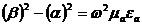 , (*)
, (*)
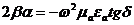 (2.29)
(2.29)
Екінші теңдеуде жалған бөлімін алып және бірінші бөлімге қойамыз:
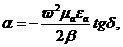
 , (2.30)
, (2.30)
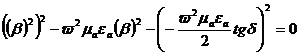 (2.31)
(2.31)
Квадраттық теңдеуді шешеміз:
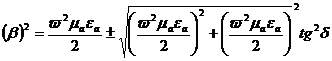 ,
,
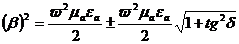 . (2.32)
. (2.32)
Сол жағында квадратқа орнатқан мәні тұрғандықтан, бұл қатынаста "+" мәні есептелінеді. Онда:
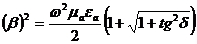 ,
,
Осы жерден аламыз: 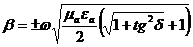 (2.33)
(2.33)
Жүйені қолданып (*), жалған бөлімі
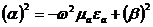 . (2.34)
. (2.34)
(2.32)-ны (*) қойамыз.
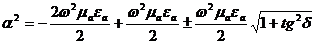 ,
,
 . (2.35)
. (2.35)
Сол бөлімі квадратқа орналғандықтан, оң бөлімі теріс болмайды. Аламыз :
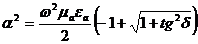 ,
,
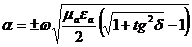 (2.36) Экспоненциальдық көбейткішті
(2.36) Экспоненциальдық көбейткішті 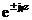 анализдаймыз. Қойып :
анализдаймыз. Қойып : 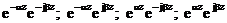 осы мәнді алуға болады. Физикалық нақтылық бірінші және екінші туынды болады. Біріншісі z ось оң бағытта таралған өшу толқынына сәйкес, ал соңғысы - z ось теріс бағыттағы. Демек , тегіс толқындық өріс жоғалту ортасында таралатын , келесі жүйеде көрсетіледі:
осы мәнді алуға болады. Физикалық нақтылық бірінші және екінші туынды болады. Біріншісі z ось оң бағытта таралған өшу толқынына сәйкес, ал соңғысы - z ось теріс бағыттағы. Демек , тегіс толқындық өріс жоғалту ортасында таралатын , келесі жүйеде көрсетіледі:
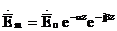 (2.37)
(2.37)
Осы жағдайда ортаның сипаттамалық кедергісі комплекстік өлшем болып табылады.
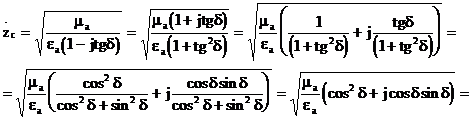
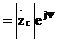 . (2.38)
. (2.38)
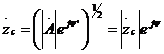 ,
,
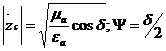 (2.39)
(2.39)
мұндағы 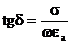 - диэлектикалық жоғалтудың тангенс бұрышы.
- диэлектикалық жоғалтудың тангенс бұрышы.
Тең фазаның беті z =const теңдеуімен анықталады. Тең амплитуданың беті тең фазаның бетімен сәйкес келеді, қарастырылып отырған процесс тегіс біртекті толқын болып табылады.
Өрістің құраушысы бар, толқынның таралу бағыты өзара-ортогональдық және перпендикулярлық, ол көлденең болады. Толқынның амплитудасы таралу барысында экспоненциальды азайтады. Осы жағдайда магниттік өрістің құраушысы электрлік бұрыштан 0 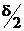 қалып отыр
қалып отыр
Электромагниттік толқынның негізгі сипаттамаларын қарастырамыз.
Фазалық жылдамдығы төмендегі теңдеуге тең
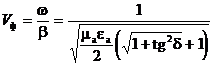 (2.40)
(2.40)
Бұл теңдеуден шығатыны, b>k, фазалық жылдамдық ортада жоғалтумен аз фазалық жылдамдық ортада жоғалтусыздан қарағанда, себебі 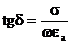 .
.
Фазалық жылдамдық жиілік функциясы болып табылады. Жиіліктің өсуіне байлынысты tgd азаяды және фазалық жылдамдық жоғарылайды. Фазалық жылдамдық ортаның өткізгішіне байланысты. Өткізгіштің өсуі tgd жоғарылайды және фазалық жылдамдық азаяды.
Толқын ұзындығы осылай анықталады
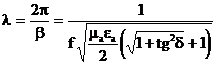 (2.41)
(2.41)
Жүйеден (2.41) көрінеді, l ортада жоғалту аз болса l бұл ортада жоғалту болмайды. Өткізгіштің өсуіне байланысты tgd өседі және l азаяды. Толқын таралуы эенргия тасымалы арқылы жүргізіледі. Пойнтинг векторы
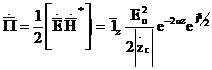 (2.42)
(2.42)
Энергия таралу жылдамдығын есептейміз
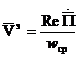 (2.43)
(2.43)
Ең басты принципиальдық айырмашылығы Vф , VЭ , zс ортада жоғалтусыз әрбір жиілікте өзгеріссіз және ортаның электродинамикалық параметрімен анықталады. Ортада жоғалтумен бұл параметрлер жиіліктің функциясы болады. Электромагниттік толқынның параметрлерінің жиіліктен байланысы дисперсия деп атайды, ал жанасымды ортада диспергирлік деп атайды. Дисперсия жоғалтуы жоқ ортада болуы мүмкін, егер бірде бір электродинамикалық параметрлер жиілік функциясы болса.
Электромагниттық толқынның нақты ортадағы екі жағдайын қарастырамыз, тегіс толқынның нақты диэлектрлік және металлдық параметрлерін анықтаймыз.
2.4. Толқынның нақты диэлектрлікте таралуы
Нақты диэлектрик үшін

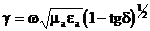 .
.
Онда фаза коэффициенті және өшу коэффициенті осындай түрде болады:
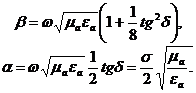 (2.44)
(2.44)
b қолдана отырып, аламыз:
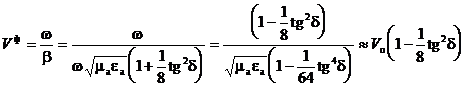 , (2.45)
, (2.45)
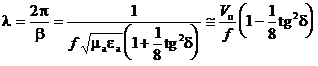 , (2.46)
, (2.46)
мұндағы Vо — ортадағы жарық жылдамдығы.
Қорытындылай келе, тегіс толқынның параметрі нақты диэлектрикте жоғалту жоқ ортаның параметрімен ерекшелінеді. Тұрақты өшу α нақты диэлектрикте өте кіші өлшем бірлік болып табылады және жиілікке қатысты емес.
2.5. Толқынның нақты металлда таралуы
Өткізгіш ортада 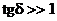 .
.
Бірлікті сақтап, аламыз:
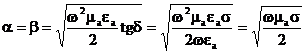 . (2.47)
. (2.47)
b және a сызықты емес w қатысты, өзгеруіне байланысты w олар өзгереді.
Фазалық жылдамдық үшін
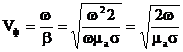 (2.48)
(2.48)
және толқын ұзындығы үшін
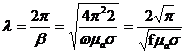 . (2.49)
. (2.49)
Кедергілік сипаттамасы:
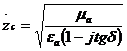 , (2.50)
, (2.50)
бірлікті сақтап, аламыз
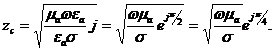 (2.51)
(2.51)
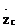 нақты және жалған бөлім үшін қарастырамыз:
нақты және жалған бөлім үшін қарастырамыз:
 . (2.52)
. (2.52)
Тегіс толқын параметрін вакуумда және мысты жиілікте f =1МГцсалыстырамыз
| Vф=VЭ=421 м/сек l=4,21*10-6 м zс=3,74*10-4 Ом |
| вакуум Vф=VЭ=3*108 м/с l=300 м zc=120p=377 Ом |
Нақты өткізгіште электромагниттық толқында өте күшті жұту болады. Мыста f = 1МГц жолында 1 мм өшуі құрайды
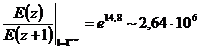 (2.53)
(2.53)
Металлды айнымалы электромагниттік өрісті қалқалау кезінде қолдануға болады.
2.6. Толқын поляризациясы
Поляризация жазықтық-уақыттық электрлік өрістің кернеу векторын бағдарлауын сипаттайды Е. Жазықтық, Е векторы арқылы өтетін және толқын таралу бағытын поляризация тегістігі деп атайды. Тегістік толқынды қарастырайық z осьі оң бағытында таралатын.
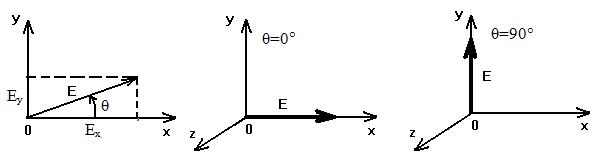
Сурет.2.1 Сурет. 2.2 Сурет.2.3
Е векторы теістіктің
түсуі Көлденең Тік
поляризация поляризация
Е вектор осындай толқынды хоу жазықтығында жатадыжәне екі проекциясы болады, фаза бойынша қозғалған φ өлшем бірлігіне.
E=x°Ј0xcos (ωt—kz)-у°Eоy.cos(ωt-kz-φ) (2.54)
Ориентацию вектора Е векторының бағдарлауы жазықтықта бұрышпен қою оңай
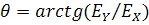 (2.55)
(2.55)
Е векторымен xoz жазықтығы арасын көлденең санаймыз
Берілгеніне байланысты E0X, Е0Y және φ (2.54) поляризацияның бірнеше түрін қарастыруға болады:
1. φ=0 и Еоx ≠Е0y. Келіскендей (2.54) және (2.55) θ=arctg(E0y/E0x). Вектор Е жазықтықта орналасқан , бұрышына иілген θ көлденең жазықтықта (сурет. 2.1). Поляризация тегістік және сызықтық деп аталады.
Жиі кезде, θ=0 (сурет.2.2) немесе θ=90° (сурет.2.3), сызықтық поляризация көлденең және тік деп аталады.
2. φ=90° және Е0х=Еоу=Е0. Бұл кезде
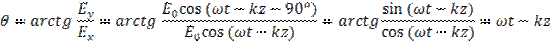 (2.56)
(2.56)
θ бұрышы кеңістікте уақыт бойынша өзгереді, ал поляризация жазықтығы айналады. z=const тең болғанда Е векторыω бұрыштық жылдамдықпен айналады, ал оның аумағы озгеріссіз қалады

Е векторының ұшы жазықтықтағы z=const шеңберді сипаттайды (2.4 а сурет), б кеңістіктегі шеңбер тектес спираль (2.4 в сурет). Поляризация шеңбер тектес деп аталады. Шеңбер тектес поляризацияның екі көрінісін көрсетеді: оң жақ, Е векторы толқын таралуымен сағат тілімен бағыттас (2.4, а сурет), және сол жақ- Е векторы сағат тіліне қарсы бағытталады (2.4, б сурет). Толқынның оң жақ поляризациясын Е+арқылы белгілейді, ал сол жақты Е -. Оң жақ айналым φ = 90° болған жағдайда болады, ал сол жақ φ = —90 болғанда.
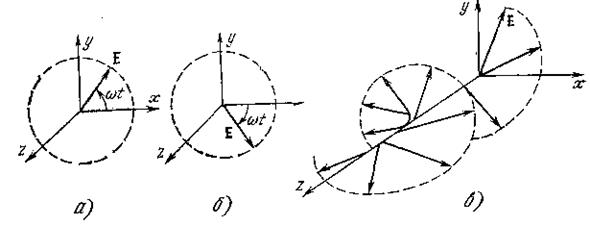
2.4 сурет Шеңбер тектес поляризация: сол және оң жақ айналым
3. Егер φ=±90° және Еох≠Еоу, Е векторы жазықтықта z=const бойынша айналады, бирақ оның ұзындығы өзгереді. Нәтижесінде Е векторының ұшы эллипсті сипаттайды , ал поляризация эллипс тектес поляризация деп аталады.(2.5 сурет). Фазаның жылжуы кезінде толқын элиппс тектес поляризация болып қала береді, бірақ эллипс осі х осіне γ бұрышына бұрылған (2.6 сурет), келесі формулада көрсетілген
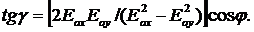 (2.57)
(2.57)
Шеңбер тектес толқын поляризациясы радиотехника және байланыста кең қолданылады. Айналмалы поляризация толқының қозуы үшін мұндай толқынның екі сызықты-поляризанған векторлары Е кеңістікте ортогональді болатын, амплитудалары бойынша тең және фаза бойынша 90 градусқа жылжыған толқындардың қосылуынан туғанын ескерген жөн.

2.5 сурет Эллипс тектес поляризация 2.6 сурет х осі мен γ бұрышы бойынша эллипстің эллипс тектес поляризациясы
Сызықтық поляризацияланған толқынды кері бағытта айналған және Е векторының бирдей амплитудасы ретінде екі толқынның шеңбер тектес поляризациясын суперпозиция ретінде ұсынуға болады. Әр түрлі ось бойынша толқынның таралу шығысында векторлық диаграммалары (2.7 сурет) көркемдейді.
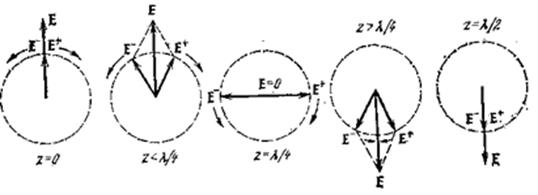
Рис.2.7 Векторлық диаграммалар
3. Екі ортаның шекарасында толқындық көріністердің тарауы
3.1. Еркін бағдарлы жазық толқындар
Алдыңғы парагафтарда декарталық жүйенің осьтерінде таралған жазық толқындарды қарастырған болатынбыз.
Орта шығындарсыз деп болжаймыз. Толқынның электрлік және магниттік құраушыларын қарастырайық.
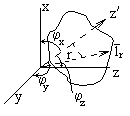
Сурет. 3.1 Цилиндрлік жүйедегі жазық толқын
мұнда:
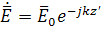 ,
,
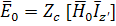 ,
,
мұнда: 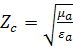 ,
,
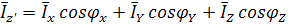 (3.1)
(3.1)
Толқынның бағытын айқындайтын бұрыш косинустары бағыттаушы деп аталады.
Фазалық жазықтықтың теңдеуі( 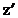 =const):
=const):
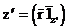 ,
,
мұнда 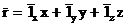 (3.2)
(3.2)
Онда скалярлық туындысы:
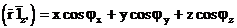 (3.3)
(3.3)
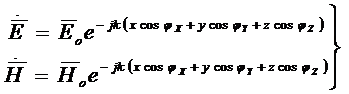 (3.4)
(3.4)
Орта шығынсыз деп болжаған болатынбыз. Ортада шығын болған жағдайда теңдеу өзгермейді, тек k-ның орнына g=b-ja қойылады. Қарастырмай тұрып толқындық көріністерге анықтама берейік.
Жазықтық, шекараға нормаль арқылы қатарлас өтетін, құлау жазықтығы деп аталады. Вектор  толқынның таралу бағытына перпендикуляр, ал толқынның құлау жазықтығына қатысты ол еркін түрде бағытталады.
толқынның таралу бағытына перпендикуляр, ал толқынның құлау жазықтығына қатысты ол еркін түрде бағытталады.
Пікірлердің жалпы түрін жоғалтпай, вектор  бағытының екі жағдайын қарастырсақ жеткілікті:
бағытының екі жағдайын қарастырсақ жеткілікті:
1)  векторы құлау жазықтығына перпендикуляр (бір қалыпты поляризация);
векторы құлау жазықтығына перпендикуляр (бір қалыпты поляризация);
2)  векторы құлау жазықтығына параллель (қатарлас поляризация).
векторы құлау жазықтығына параллель (қатарлас поляризация).
Вектор  -нің еркін бағыты кезінде, ол осы екі жағдайдың суперпозициясы түрінде түсіндіріледі.
-нің еркін бағыты кезінде, ол осы екі жағдайдың суперпозициясы түрінде түсіндіріледі.
3.2. Жазық толқынның екі диэлектрлік шекараға құлауы
Кіріспе ескерту
Жазық толқынның 3.2 суретте көрсетілгендей жазық орталарға құлауын қарасстырайық. Мысалы, орталарда шығындар жоқ деп ойлайық. Яғни құлау жазықтығы координаталардың декарттық жүйесінің xоy жазықтығымен сәйкес келеді деп есептейміз. Таралудың бағытталған бұрышы мен х осі арасындағы бұрыш – құлау бұрышы деп аталады. Орталардың шекаралары yоz жазықтықтарымен сәйкес келеді.
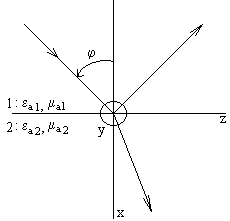
3.2 сурет Жазық толқынның жазық шекараға құлауы
Бағыттаушы косинустар келесі теңдеу бойынша анықталады:
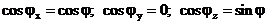 ,
,
т.е. фазалық көбейткіш 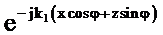 ,
,
мұнда : 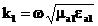 .
.
3.3. Бір қалыпты поляризация
Барлық жағдайда :
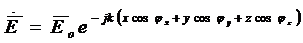 (3.5)
(3.5)
Бір жағдайда Е векторы у осі сияқты бағытталған .
Фазалық көбейткіш -  ;
;
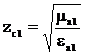 .
.
Құлау толқынының теңдеуін жазуға болады. Бастапқы ескертпелерді (3.5) және (3.6) өрнектеріне қойсақ онда өрнек
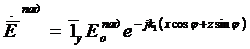 (3.6)
(3.6)
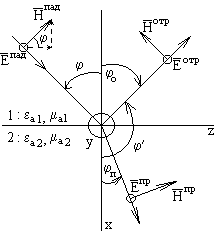
3.3 сурет Бір қалыпты поляризация
Ортақ жағдайда толқынның шекараға түсу нәтижесінде түскен толқан толығымен немесе біртіндеп шағылады немесе сынады.
Әрине бұл жерде шағылған немесе сынған толқын сол сияқты жазық, сызықты поляризацияланған деп санауға болады. Құлаған, шағылған және сынған толқынның таралу бағыты хоz жазықтығында жатыр деп ойлаймыз. Одан басқа, шағылған және сынған толқын, түскен толқын сияқты нормальді позяризацияланған болып табылады. Онда шағылған және сынған толқындар үшін төмендегідей жазуға болады:
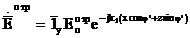 (3.7)
(3.7)
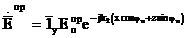 (3.8)
(3.8)
мұнда 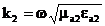 ;
; 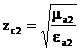 .
.
Бұл жағдайда құлаған толқынның j, 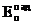 мінездемелері белгілі. Ізделіп өтырған шамалар j¢, jn,
мінездемелері белгілі. Ізделіп өтырған шамалар j¢, jn, 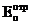 ,
,  . Егер тапсырманы шешу барысында біз келесі шекаралық шарттарды қанағаттандыратын шаманы алатын болсақ
. Егер тапсырманы шешу барысында біз келесі шекаралық шарттарды қанағаттандыратын шаманы алатын болсақ
 ;
; 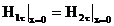 (3.9)
(3.9)
онда, бірліктілік теоремасына сәйкес, табылған шешім дұрыс және жалғыз мүмкін мән болып табылады. (3.9) қатынасы орталардың шекара бөліктерінің барлық нүктелерінде орындалуы тиіс, ол z осімен сәйкес, яғни кез келген z кезінде (3.9) шарты орындалуы тиіс. Ол егер түскен, шағылған және сынған толқындар z бойынша бірдей тәуелділікке ие болса ғана мүмкін.
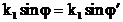 (3.10)
(3.10)
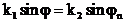 (3.11)
(3.11)
j¢ бұрышы 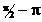 шектерін, ал j бұрышы
шектерін, ал j бұрышы 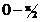 шектеріне ие екенін ескере отырып, бір төмендегі тұжырымға келеміз,
шектеріне ие екенін ескере отырып, бір төмендегі тұжырымға келеміз,
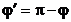 (3.12)
(3.12)
Осыған ұқсас тапсырмаларды жіктеген кезде әдетте бұрышты j¢ емес, қосымша бұрышты jо - шағылу бұрышын жиірек қолдануды дұрыс көреді.
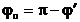 (3.13)
(3.13)
(3.12) қатынасын (3.13)-ке қойым, алатынымыз
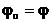 (3.14)
(3.14)
(3.14) формуласы – Сннелиустың бірінші заңы, ол құлау бұрышы шағылу бұрышына тең деп айтады.
(3.11) теңдеуін қолдансақ, төмендегі қатынастарды аламыз:
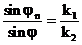 (3.15)
(3.15)
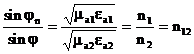 (3.16)
(3.16)
(3.15) теңдеуі (3.16) түрінде жазылған, ол Снеллиустің екінші заңы деп аталады, бұл жерде: құлаудың синус бұрышының шағылудың синус бұрышына қатынасы бірінші және екінші орталардағы шағылу коэффициенттерінің қатынасына тең дегенді білдіреді.
Шағылудың синус бұрышының құлау синус бұрышына қатынасы сынудың қатысты коэффициентіне тең. Шекаралық шарт (3.9) келесі түрде жазылады:
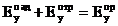 , x = 0 (3.17)
, x = 0 (3.17)
бұл жерде бірінші ортадағы тангенциалды компоненттер құлаған және шағылған толқындар арқылы пайды болады, ал екінші ортадаға тангенциалды компоненттер сынған толқындармен пайда болатыны ескерілген. (3.17) және (3.18) теңдеулеріне (3.3)-(3,8) теңдеулерінен сәйкес компоненттерді қойып,
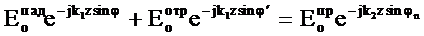 (3.18)
(3.18)
 (3.19) аламыз.
(3.19) аламыз.
Z бойынша бірдей тәуелділікті ескере отырып, барлық фазалық көбейткіштер бірдей және олар қысқартуға болады деп белгілейік. 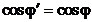 , аламыз:
, аламыз:
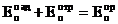 (3.20)
(3.20)
 (3.21)
(3.21)
Шағылысқан және сынған толқынның амплитудасы 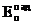 пропорционал, содан:
пропорционал, содан:
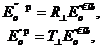
мұнда 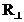 — шағылысу коэффициенті ,
— шағылысу коэффициенті , 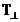 — сыну коэффициенті .
— сыну коэффициенті .
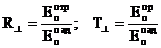 ,
,
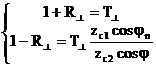 (3.22)
(3.22)
Бұл жүйені шеше отырып, аламыз:
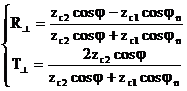 (3.23)
(3.23)
Шағылысу және сыну коэффициенттерін Френель коэффициенті деп жиі атайды.
3.4. Қатарлас (параллельная) поляризация
Жазық сызықты поляризацияланған толқынды қарастырайық.  векторы құлау жазықтығында болады (бірінші жағдай сияқты).
векторы құлау жазықтығында болады (бірінші жағдай сияқты).
Құлау, шағылған және сынған толқындарға арналған өрнек:
 х £ 0 (3.24)
х £ 0 (3.24)
 , х £ 0 (3.25)
, х £ 0 (3.25)
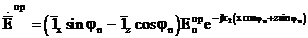 , х ³ 0 (3.26)
, х ³ 0 (3.26)
j¢, jn, 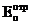 ,
, 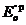 белгісіз болып табылады. Олар шекаралық өрнекті шешкен уақытта табылады:
белгісіз болып табылады. Олар шекаралық өрнекті шешкен уақытта табылады:
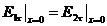 (3.27)
(3.27)
Бұл жағдайда арақатынас келесі түрде жазылады (3.27) :
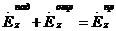 , х = 0 (3.28)
, х = 0 (3.28)
(3.27), (3.28) арақатынасы барлық шекара нүктелерінде орындалу керек, z координатаның барлық мәнінде. Бұл шарт түскен, шағылған және сынған толқындар z-тан бірдей тәуелді болса ғана орындалады, яғни:
 (3.29)
(3.29)
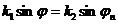 (3.30)
(3.30)
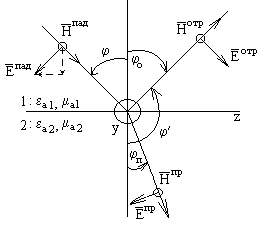
3.4 сурет Қатарлас (параллельная) поляризация
(3.29), (3.30) қатынастарынан Снеллиуса заңдары шығады:
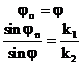 ,
,
Яғни Синнелиус заңдары түскен толқын поляризациясына бейтарап келеді.
(3,28) қатынасын сәйкес формулаға қойып, өріс проекциясы үшін келесі түрде жазамыз:
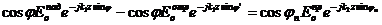 (3.31)
(3.31)
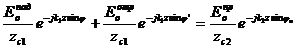 (3.32)
(3.32)
(3.29), (3.30) формулаларынан барлық экпоненталар тең екенін көреміз. Қысқартамыз, келесі формулаларды аламыз:
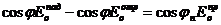 (3.33)
(3.33)
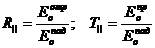 .
.
Онда арақатынастарды басқаша жазуға болады (3.33):
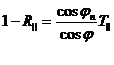 (3.34)
(3.34)
 (3.35)
(3.35)
Жүйені шеше:
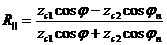 (3.36)
(3.36)
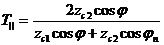 аламыз. (3.37)
аламыз. (3.37)
— қатарлас(параллель) поляризацияға арналған Френель коэффициенті.
j косинусын шығаруға болды

Бір қалыпты және қатарлас поляризацияға арналған Френель коэффициентін салыстыратын болсақ, онда әр түрлі поляризацияға Френель коэффициенті түрлі екенің байқауға болады.
Бұл жағдайда егер жазық толқын а жазықтығына нормаль берсе, жазықтықтың құлауы мағынаны жоғалтады. Бұл жағдайда берілу бұрышы, шағылу бұрышы және сыну бұрышы нөлге тең болады. Сонда Френель коэффициенті өрнегі жеңілдейді:
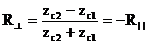 ,
,
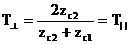 . (3.38)
. (3.38)
3.5. Толқынның екінші ортаға өтудің толық шарты
Брюстер бұрышы
Толқынның толық сыну нәтижесінде бірінші ортаға әсері байқалмайды және шағылыс коэффициенті нөлге тең болады. Қатарлас поляризацияның жағдайын қараймыз:
 (3.39)
(3.39)
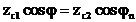 . (3.40)
. (3.40)
Құлау бұрышының косинусын синус арқылы жазсақ, содан он жақ және сол жақ өрнекті квадраттасақ
 , аламыз. (3.41)
, аламыз. (3.41)
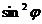 біркелкі шеше :
біркелкі шеше :
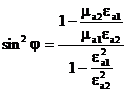 (3.42)
(3.42)
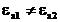 аламыз.
аламыз.
Шынайы диэлектриялық орта үшін өрнек орындалады: 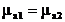 (*)
(*)
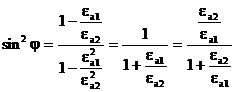 (3.43)
(3.43)
Белгілі тригонометриялық барабарлықты еске ала:
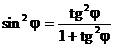 ,
,
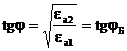 (3.44)
(3.44)
аламыз.
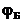 бұрышы, Брюстер бұрышы , және де толық поляризация бұрышы деп аталады.
бұрышы, Брюстер бұрышы , және де толық поляризация бұрышы деп аталады.
3.6. Екі ортаның шекарасынан толық шағылыс.
Екі диэлектрлік орта
Ортаның шекарасында сынған толқындардың болмау шарттарын анықтаймыз. Толық ішкі шағылыстың нәтижесі туады. Сыну бұрышы 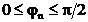 арасында өзгереді. 90° тең сыну бұрышының түсу бұрышы критикалық бұрыш деп аталады.
арасында өзгереді. 90° тең сыну бұрышының түсу бұрышы критикалық бұрыш деп аталады.
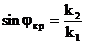 (3.45)
(3.45)
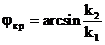 (3.46)
(3.46)
3.6 Екі ортаның шегінен толық шағылыс.
Екі диэлектрлік орта
Орта шегінде жоқ сынық толқынның шартын анықтаймыз, яғни, ішкі шағылудың толық эффектісі пайда болады. Сыну бұрышы 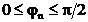 аралығында өзгереді. 90°-қа тең сыну бұрышының мәні сындық бұрыш деп аталады.
аралығында өзгереді. 90°-қа тең сыну бұрышының мәні сындық бұрыш деп аталады.
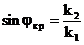 (3.45)
(3.45)
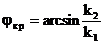 (3.46)
(3.46)
Түсу бұршының одан әрі көбеюінде, 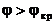 болғанда, түспе толқынның кез-келген поляризациясында шағылу коэффиценті 1-ге тең болады:
болғанда, түспе толқынның кез-келген поляризациясында шағылу коэффиценті 1-ге тең болады:
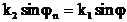 . (3.47)
. (3.47)
Онда 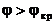 жағдайында төмендегі теңсіздік сақталуы керек:
жағдайында төмендегі теңсіздік сақталуы керек:
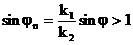 (3.48)
(3.48)
Бұрыш 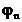 -ның шынайы мәнінде бұл теңсіздік болмайды. Содықтан,
-ның шынайы мәнінде бұл теңсіздік болмайды. Содықтан, 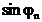 1-ден үлкен болуы үшін
1-ден үлкен болуы үшін 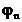 шамамен комплекстік бірлік болып табылады. Сонда:
шамамен комплекстік бірлік болып табылады. Сонда:
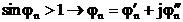 (3.49)
(3.49)
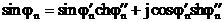 (3.50)
(3.50)
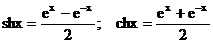 ,
,
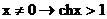 .
.
Біз осы қасиетті пайдаланамыз. Осы байланысты орындау үшін (3.48) керек, сонда:
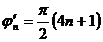 ,
, 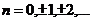 ,
,
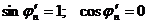 , (3.51)
, (3.51)
яғни 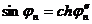 ,
,
сонда 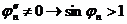
(3.51)-ден энергияның тығыздық ағыны шағылған және түспе толқында бірдей екенін көреміз.
3.7. Ішкі толық шағылыстың шарты.
1 шарт: 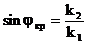 өйткені sinj<1 то k2<k1– екінші орта тығыздығыоптикалық түрде біріншісінен азырақ болуы керек.;
өйткені sinj<1 то k2<k1– екінші орта тығыздығыоптикалық түрде біріншісінен азырақ болуы керек.;
2 шарт: 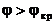 . Қорытынды толқынның құрылым алаңына бірінші ортада
. Қорытынды толқынның құрылым алаңына бірінші ортада 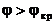 теңсіздігін аламыз.
теңсіздігін аламыз.
|
|
 ,
, 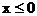 ; (3.52)
; (3.52)
|
|
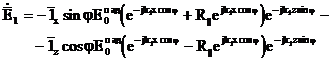 ,
, 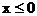 ; (3.53)
; (3.53)
Біздің жағдайымызда 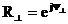 ,
, 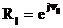
Орам байланысы үшін көбейткішті жақша сыртына шығару керек 
Орындалған озгерістерді есепке алғанда:
|
|
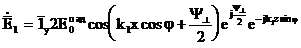 ,
, 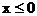 ; (3.54)
; (3.54)
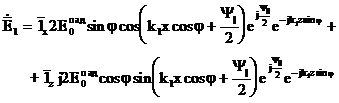 ,
, 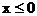 ;(3.55)
;(3.55)
|
|
Алынған ара-қатынастан шығады:
1. Олар тегіс электромагниттық толқынды суреттейді;
2. Әр түлі фазалардың беті бірдей жазықтықты құрайды;
Перпендикулярлық ось z, яғни, z = const теңдеуімен анықталады;
3. Жазық толқындардың амплитудасы j бұрышының құлауына және хкоординатына тәуелді;
4. Бірдей амплитуданың бірдей беті x = const теңдеуімен анықталады;
5. Бірдей амплитуданың беті әр түрлі фазаның бетімен сәйкес келмейді; 6. жазық толқын бiртектi емес болып келеді;
7. Жазық толқындар бірінші ортада z осі бойында таратылады, яғни, a шегінің бойында, ондай толқындар бағыттаушы деп аталады.
Әрі перпендикуляр, әрі параллель жағдайындағы поляризацияда жазық толқындар таратушының бағытында құраушы алаңға ие болады (перпендикулярлық поляризация жағдайында Нz, ал параллельдық поляризация жағдайында Ez), яғни, алынған қорытынды жазық біртекті толқынды көрсетеді.
Фазалық жылдамдықты анықтайық.
Жалпы көрініс
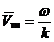 . (3.56)
. (3.56)
Біздің жағжайда
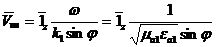 (3.57)
(3.57)
Анализ жасаймыз 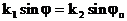 ,
,
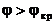
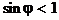 ;
; 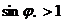 ,
,
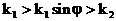 ,
, 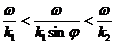 ,
,
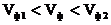 (3.58)
(3.58)
(3.58) анықтамадан бағыттаушы толқын фазалық жылдамдықпен таралатынын көреміз.
Таратылатын бағытта толқын ұзындығын анықтаймыз: 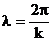 ,
,
Немесе осы жағдайда:
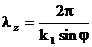 (3.59)
(3.59)
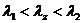
 қатынасынан перпендикулярлық шекарасы бағытында (параллель ось х), шекара тік тұрған кеңістіктік периодты толқын түріне ие болады
қатынасынан перпендикулярлық шекарасы бағытында (параллель ось х), шекара тік тұрған кеңістіктік периодты толқын түріне ие болады
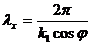 .
.
Осы қатынастарға қарап, көлденең бағыттаушы толқынның таралу алаңының компоненты ( 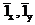 ) – синфазалық екенін атап өтуге болады. Бойлық көлденеңге қатысты 90 (z) фазалық ауытқуға ие.
) – синфазалық екенін атап өтуге болады. Бойлық көлденеңге қатысты 90 (z) фазалық ауытқуға ие.
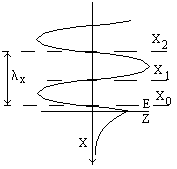
Сурет 3.5 Толқынның екінші ортаға өтуі.
Пойтингтың комплекстық векторын анықтайық.
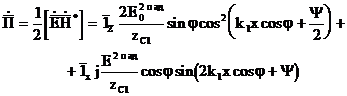 (3.59)
(3.59)
"+" таңбасы (3.59 ) анықтамадан қалыпты поляризацияға сәйкес келедi, ал
"-"белгісі поляризацияға сәйкес келеді. (3.59) анықтамадан, Пойтингтың комплекстық векторы нақты және жорамал бөлікке ие.
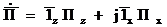
Пойтинг векторының период үшін орташа мағынасы z осі бойымен бағытталған.
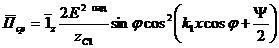 (3.60)
(3.60)
Яғни, орташа алғанда бір периодта энергия z осі бойымен бағытталады. Перпендикулярлық шекара бағытында қуаттың реактивті ағыны болады.
Бұл жазықтықтардың x осімен қиылысу нүктесін келесі теңдеуден анықтауға болады.
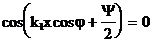 .
.
Поляризация жағдайында параллельдік шекарада Еzкомпоненты болады. Бұдан алдыңғы теңдеуден кейін мына теңдеу келеді:
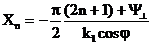 (3.61)
(3.61)
мұндағы n=1, 2, 3, … .
Жазықтықтық параллельдік a шекарасында орны көрсетілген (3.61) анықтамасында қанағаттандыратын шекаралық шарттар (Еt=0, Нn=0) мінсіз өткізгіш бетіндегі шарттарға сай келеді.
Егер біз осы жазықтықтың біреуін мінсіз өткізетін (хn)-мен алмастырсақ, онда, мынаны аламыз  (яғни, бірінші ортада жазықтықтың үстінде) алаң өзгеріссіз қалады.
(яғни, бірінші ортада жазықтықтың үстінде) алаң өзгеріссіз қалады.
Осы жазықтықтардың тағы бір ерекшелігі (3.61) осы беттен өтетін энергияның ағыны (әрі активті, әрі реактивті) нолге тең.
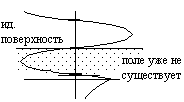 |
Сурет3.6 Энергияның бірінші ортада таралуы.
Бірінші ортада мына жағдайда 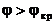 , энергетикалық трубканы бөліп аламыз, яғни, кеңістіктің бір бөлігі, жанама бет арқылы энергияның тасымалы, яғни,
, энергетикалық трубканы бөліп аламыз, яғни, кеңістіктің бір бөлігі, жанама бет арқылы энергияның тасымалы, яғни, 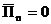
Энергетикалық трубка ретінде кеңістіктің бірдей беттермен шектелген бөлігін алған ыңғайлы және былай анықталады(3.61). Мысалы: xn , xn+1.
Бұл жағдайда құраушы алаң х координатына тәуелді екенін ескерсек, таралу жылдамдығының мәні үшін энергия интегралдауды өзіне қосады. Келесі компонентке қарай отырып және интегралдауды жүзеге асырып, мынаны аламыз:
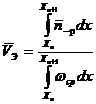 (3.62)
(3.62)
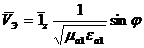 (3.63)
(3.63)
Энергияның таралу жылдамдығы бірінші ортада бірінші ортадағы жарық жылдамдығынан кіші екені (3.63)-тен көрінеді.
Фазалық жылдамдық үшін қорытынды
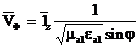
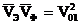 .
.
Екінші ортада өріасті талқылайық.
Бастапқы қатынастар:
|
|
 ,
, 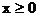 (3.64)
(3.64)
|
|
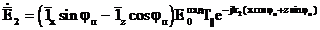 ,
, 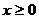 (3.65)
(3.65)
Егер 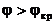
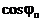 жорамал өлшем болады.
жорамал өлшем болады.
Белгілеу енгізген ыңғайлы:
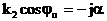 (3.66)
(3.66)
a егер 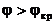 нақты өлшем болады:
нақты өлшем болады: 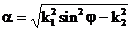
Снеллиус заңынан:
 ,
,  ,
,
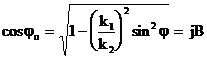 ,
, 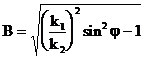 ,
, 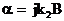 .
.
(3.66) минус таңбасы физикалық ұғынудан алынған
(3.66)-ны (3.62) - (3.65)-ға қоя отырып 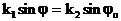 алатынымызды ескерген жөн:
алатынымызды ескерген жөн:
|
|
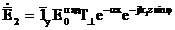 ,
, 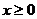 (3.67)
(3.67)
|
|
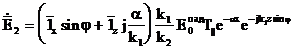 ,
, 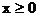 (3.68)
(3.68)
(3.67) - (3.68)-ден көрініп тұр, 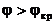 екінші ортадағы (әр түрлі фазаның беті z=const теңдеуімен анықталады) шекара бойында таралатын алаң жазық толқынға ие.
екінші ортадағы (әр түрлі фазаның беті z=const теңдеуімен анықталады) шекара бойында таралатын алаң жазық толқынға ие.
Бірдей амрлитуданың беттері (x=const) әр түрлі фазаның беттеріне перпендикуляр (z= const), яғни, жазық толқын біртекті емес болады.
z осі бойы бағытында таралатын алаңның құраушылары (Нzперпендикулярлық поляризация және Ez параллель поляризация жағдайында), яғни, жазық біртекті толқын қиылыспаған болады. Толқынның фазалық жылдамдығы және толқын ұзындығы бірінші ортадағы толқынға арналған қатынастармен анықталады.
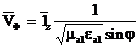 ,
, 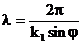 ,
,
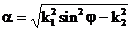 ,
, 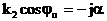 .
.
Тән өзгешелік: жазық толқынның амплитудасы шекараға қарай экспоненциальды төмендейді, яғни, алаң кейбір шекара бойындағы қабатта болады. Бағытталатын толқындар амплитудалары шекарадан алыстаған сайын экспоненциальды өше бастайды, ол беттік едп аталады.
Перпендикулярлық шекара ортасы бағытындағы амплитуданың толқын кемуін сипаттайтын a — коэффициент қай кезде өзгерететін анализ жасап көрейік.
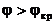 жағдайында a шынайы коэффицент болады. Өзгеріс жағдайында
жағдайында a шынайы коэффицент болады. Өзгеріс жағдайында
 a изменяется так
a изменяется так 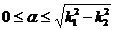 .
.
Энергияның таралу жылдамдығын анықтау үшін 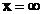 бастап
бастап  -ге дейін энергетикалық трубканың бір бөлігін алған жөн.
-ге дейін энергетикалық трубканың бір бөлігін алған жөн.
Бірінші ортадағы Пойтинг векторы:
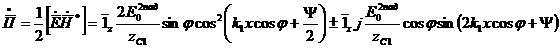
Энергияның таралу жылдамдығы екінші ортадағы теңдеу және бірінші ортадағы теңдеу бірдей қатынаспен анықталады.
Беттік эффект
4.1. Беттік эффекттің пайда болуы.
Айнымалы электромагниттық өріс және ток тығыздығының өткізу көлемі өткізуші ортада шекарадан ( 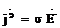 ) экспоненциалды түрде алыстаған сайын кеми беретіні өткен параграфта көрсетілген болатын. Яғни, ток және алаң жоғарғы жиілікте жіңішке шекаралық қабатта шоғырланған болады. Бұл құбылыс бетттік немесе эффект-скині деген атқа ие болды.
) экспоненциалды түрде алыстаған сайын кеми беретіні өткен параграфта көрсетілген болатын. Яғни, ток және алаң жоғарғы жиілікте жіңішке шекаралық қабатта шоғырланған болады. Бұл құбылыс бетттік немесе эффект-скині деген атқа ие болды.
Өткізгіштің беттік эффекттік тік қиылуы геометриялық қиылудан айтарлықтай кем болады және активті кедергінің өсуіне алып келеді (сурет 4.1)
 |
Сурет.4.1 Өткізгіштің бетіндегі ток концентрациясы
4.2. Өткізгіште энергияның жоғалуы.
Анық өткізгіш бетінде 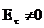 . Бұл өткізуші ортаның ішіне бағытталған энергия ағынының болуының себебі болад. Өткізгіш ортада қуат жоғалуының қатынасын аламыз.
. Бұл өткізуші ортаның ішіне бағытталған энергия ағынының болуының себебі болад. Өткізгіш ортада қуат жоғалуының қатынасын аламыз.
Өткізгіш дененің және минималды радиус қисығының өлшемі >> d (кірудің тереңдігі) деп есептейік. Бұл шарт жақындатылған шекаралық қолданудың Щукин-Леонтович шарты.
S бетінде Нt компоненті берілген деп есептейік.
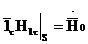
Еt Щукин-Леонтович шекаралық шартынан анықтауға болады.
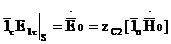
Ішкі ортаға жіберілетін Е және Н үшін энергия ағынының тығыздығын анықтаймыз.
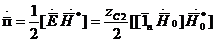 (4.1)
(4.1)
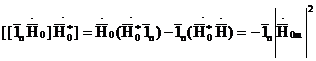 (4.2)
(4.2)
 |
Сурет 4.2 Өткізгіш шекарасы үстіндегі ток.
Осыдан
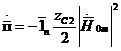 (4.3)
(4.3)
Мұнда 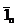 кері мәнді қабылдайды. Себебі ағын ішкі ортаға бағытталған, ал нормаль болса, ішкі ортаға қарағанда сыртқы болып келеді.
кері мәнді қабылдайды. Себебі ағын ішкі ортаға бағытталған, ал нормаль болса, ішкі ортаға қарағанда сыртқы болып келеді.
Егер дене өлшемі >> кіргізу тереңдігі d болса, онда энергия ағыны денеден өтеді. П векторын S арқылы интегралдау нәтижесінде қуаттың комплексті жоғалтуын анықтауға болады.

Векторлық элемент аумағын ескере отырып,
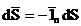 , аламыз
, аламыз
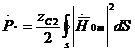 (4.4)
(4.4)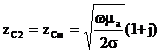
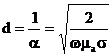
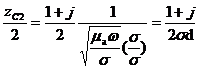 .
.
Сонда, 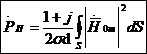 (4.5)
(4.5)
Бір период үшін комплекстік қуаттың орташа жоғалуы

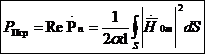 (4.6)
(4.6)
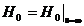

Беттік кедергілер
Тангенциалды компнент Е өткізгіш ортаның бетінде және беттік токтың тығыздық векторы бірдей бағытталған болады. Сондықтан мына қатынасты жазуға болады:
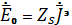 (4.7)
(4.7)
Мұндағы ZS беттік кедергі. Беттік токты ескере отырып
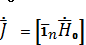 (4.8)
(4.8)
Және  (4.9)
(4.9)
Щукин-Леонтовичтың шекаралық шарты, (4.7) — (4.9) салыстырудан
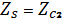 (4.10)
(4.10)
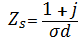 (4.11)
(4.11)
Беттік кедергінің толық бөлігін бөліп аламыз:
(4.12)
????????
(4.12) қорыта отырып, беттік эффектте өткізуші жартылай кеңістік өткізгіш қабатта қалыңдығы d, беттік эффектті есепке алмағанда, активті кедергіге ие.
Енгізілген жаңа беттік кедергіні комплекстік қуат жоғалтуы мәні үшін қолдануға болады.
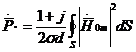
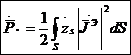 . (4.13)
. (4.13)
Сәйкесінше 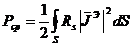 . (4.14)
. (4.14)
5 Электромагниттық толқындардың сәуле шығаруы.
5.1. Жалпы ұғым
Сәулелену ұғымында кеңістіктегі электромагниттік өрістегі энергияның энергия көзінен тасымалы түсіндіріледі. Электромагниттік өрістің кеңістіктегі тасымалдау қабілеті оның энергия сақтау заңындағы маңызды қасиетінің бірі болып табылады. Электромагниттік энергияның энергия көзінен тарамдарға бөлінуі диэлектрикта және ваккумда бола алатын ауысу тоғының арқасында болады. Сондықтан кеңістікте ауысу тоғын жасай алатын кез-келген энергия көзі электромагниттік толқындардың таратушысы болады.
Толқын таратудың мақсаты белгілі қажет емес тоқтардың бөлінуі бойынша электромагниттік толқынның тараған векторларын табу және ол әдетте қарапайым таратушылар үшін есептелінеді. Қарапайым таратушылар теориялық анализға ыңғайлы идеалды моделі болып табылады.
Айнымалы токтың линиялық элементін толқын ұзындығымен салыстырғанда азырық болса, онда ол элементарлы электрлік сәуле шығарғыш деп аталады, яғни, l кесіндісі (сурет 5.1,a) бойымен ток өтеді, яғни фазамен, амплитуданың таратылуы сәуле шығарушының бойында өзгеріссіз қалады.
Айнымалы токпен ораманы (шегі) толқын ұзындығымен салысырғында азырақ болса, онда ол элементарлы магниттік сәуле шығарушы деп аталады (сурет 5.11б)
dS фронттың элементарлы аумағында таратушы толқын:
(сурет 5.1,в) Гюйгенс элементі деп аталады.
Сфералық система координатында орындауға болады. Талдауға аумақтық сәуле таратқышы ЭЭИ қолайлы болады, оның ортасында сәуле таратқыш (сур. 5.2) орналасқан. Электромагниттің векторының сәулеленуі үш проекциядан турады:
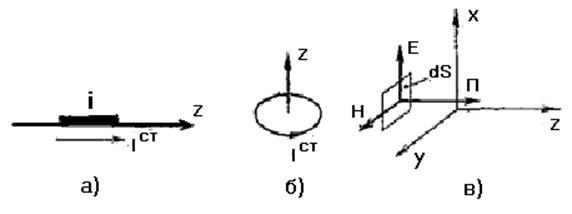
Сур.5.1.Қарапайым электрлік сәуле таратушы
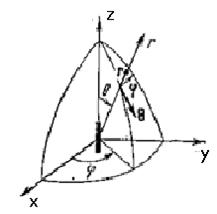
Сур.5.2. Қарапайым электрлік сәуле таратушы сфералық координатты системада
Сур.5.3.Қарапайым электрлік сәуле таратушы аумақ
 (5.1)
(5.1)
 (5.2)
(5.2)
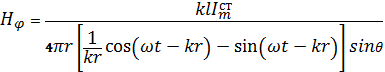 (5.3)
(5.3)
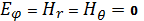 (5.4)
(5.4)
(5.1-5.4) формуласы гормоникалық электрамагнитті толқынның аумағын бейнелейді, радиалдық бағытта таратылады және күрделі кеністікті құрылымы бар. Себебі жеке аумақтын компонентінде бар әр түрлі байланысты аралық r, аумақтық зерттеуге женілдік болу үшін барлық кеністікті үш зонаға бөледі:
1) Бергi тиiстi қашықтықтарды, kr<<1
2) аралық— kr≠1;
3) алыстағы — kr>>1
Формула бойынша 5.1-5.4, жақындатылған арақатынастарды, характерлі аумаққа жақындағы және алыстағы зоны алуға болады, (kr<<1):
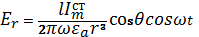 (5.5)
(5.5)
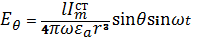 (5.6)
(5.6)
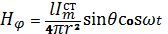 (5.7)
(5.7)
Талдауда, жақын манындағы зонада толқын характерлі болмайды (фаза кернеудін электрлік және магниттік аумақтан байланысты емес кеністікті координат). Векторы 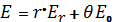 и
и  қозғалған фаза бойынша 90°. Осыдан көруге болат, тығыздықтын энергия ағыны
қозғалған фаза бойынша 90°. Осыдан көруге болат, тығыздықтын энергия ағыны
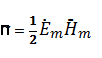
реактивті характерлі, ал ортанғы ағын энергиясы болмайды, себебі тен. Жақын арадағы зона реактивті аумақ деп аталады.
Аралық зона мына формуламен көрсетілет5.1-5.4кейде аталады сәуле таратқыш жақын арадағы аумақ деп аталат немесе дифракция Френельдін зонасы. Алыстағы зонадағы аумақ мына түрге келтіріледі:
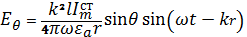 (5.8)
(5.8)
 (5.9)
(5.9)
Бұл 5.8-5.9 Еr≈0, себебі бұл вектордын Е алыстағы зонаның құраушысы.
Аумақ 5.8-5.9 сфералық толқынды көрсетіледі, себебі оның сферасы
r = const. Күштік сызықты аумақты сауле таратқыш ЭЭИ алыстағы зонада көрсетілген (сур. 5.3,а). Талдау 5.8-5.9 сфералық толқынның сипатын алыстағы зонада ЭЭИ көрсетеді:
· векторлары Е және Н перпендикулярлы, себебі Е = θЕθ , H=φHφ;
· векторлары Е және Н ортогональді бағытқа таратылатын толқын, себебі таратылады радиалды бағытта, ал векторларда болмайды радиалды құраушы (Еr= Hr = 0);
· векторлары Е және Н синфазалық;
· қарым-қатынастары амплитудалық векторлардын Е және Н байланысты сипатына
Параметр Zc характерлік кедергі толқында шексіз деп аталады. Вакумда және бос кеністікте

ЭЭИ-нен кейін алыстағы зонада бар құраушылар Eφ және Hθ, (рис.5.3,б).
5.3.Диаграмма бағыты ЭЭИ
Формуладан 5.8-5.9, амплитуда Ет және Нт байланысты екенін координаттан θ және r-дан көруге болады:
θ = 0 Em = Hm = 0, бұл кезде θ = 90° Em және Нт максималды мағына көрсетеді. Бұл түсіндіреді, егерде аумақ сәуле таратқышы ЭЭИ бағыттаса, осы характеристикаға сәйкес келсе олар енгізіледі бағытты диаграммаға (ДН).
Бағытты диаграмма — бұл график байланысты амплитудаға Ет немесе Нт бұдан бағытталған арақашықта (r = const). Сфералық система координатасында (сур.5.2) бағытталған көру нүктесіне қойылады екі бұрыштық координаттар θ және φ. Көбінесе нормиративті мағынада максималді амплитудаға жақын қолданылады,.
Функция
F(θ,φ) =Ет(θ, φ)/Етmax= Sin θ
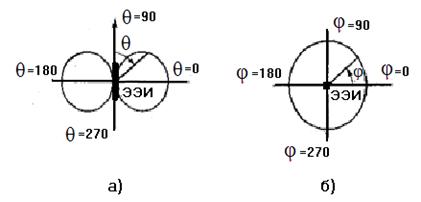
Сур.5.4 Бағыт диаграммасы ЭЭИ
Аталады нормиративті характеристика бағыты. Алынған формуладан көруге болады, аумақты ЭЭИ меридионалды бұрышқа θ және азимутальді бұрышқа φ тәуелді болады. Графиктар F (θ, φ) меридиональдіде (φ=const) (сур.5.4, а) және азимутальдіде (θ=const) (сур.5.4, б) жазықтықтарында сәйкес қолданылады.
6. Бағытталған және беткі толқын
6.1. Толық ішкі шағылысу
Практикада көп қолданылады толық шағылысу электромагниттік толқынның шекарадан бастап екі диелектрик, себебі бұл шекаралар қабілетті бағыттауға электромагниттік энергияны. Енгіземіз шарт, зерттеледі толық шағылысу,және құрылым пайда болатын толқындық процесс кезінде.
Толық шағылысу байланысты өшу сынық толқынына. Сур. 3.4көрінет, бұрыш сынығы өзгереді 0 ден бастап 90°ға дейін, мағынасыθ = 90° болады предельді. Құлау бұрышы , сәйкес келедіθ = 90°, атауға боладыграникалықжәнекритикалық(φКр).2 закон Снеллиус бойыншакөрінет, sinφкр = n1/n2. Себебі sinφKp<1, пайда болған тендік болуы мүмкін, екі диэлектр кезінде ғанаn2<n1, т.е екиншісі оптикалық катты толық емес, біріншісіне қарағанда.Егерφ>φкр, өлшем бірлігі sin θ = (n1/n2) sinφбірліктен улкен болса, жоғалтады өзінің мағыналық функциясын геометриялық бұрыштын және қарау мүмкін параметр ретінде зерттелетін прочестін.Шағылысу коэффицентін табу үшін Френель формуласын қолданамыз.
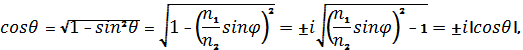 (6.1)
(6.1)
Бұл формуланы келесі түрге түрлендіреміз (формулалар 3.21 және3.22
 .
.
Санауышта және знаменательда әр бул формуладан табылады комплекстті мағына, модульдары тен болады, онда  , бұл көрсетеді толық шағылысқан толқынды зерттелген шекарадан а.
, бұл көрсетеді толық шағылысқан толқынды зерттелген шекарадан а.
Осылай, толық шағылысқан электромагниттік толқын шекарадан а бастап екі диэлектрик болуы мүмкін,біріншіден, бұрыш құлауында, улкейеді φкр, екіншіден, біріншісіне қарағанда екиншиорта азырақ толық оптикалық болады.
Толқын көрсетеді толық шағылысты нақты шекарадан бастап.Бұдан кқруге болады (3.22,3.23), себебі кедергінің характеристикасы σ2=∞ ға тен
6.2.Бірінші ортадағы аумақтағы орташа поляризации
Бірінші ортада аумақтағы E1пайда болады суперпозиция түсу аумақ ретінде және шағылысқан толқын ретінде. Себебі и , бұдан
Келесі формуладан Eпадm=y0E0e-ik1(cosφ+zsinφ)
И Eотр0= y0E0e-ik1(-xcosφ+zsinφ)бірінші аумақ мынандай түрге келтіріледі:
Ортақ көбейтіндіні жақша сыртына шығарғанда 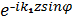 ,жіне де
,жіне де 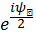 формуланы Эйлер бойынша шығарамыз
формуланы Эйлер бойынша шығарамыз
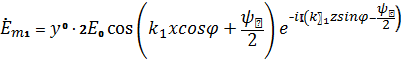
Лездік түрге келгенде
 ,
,
Пайда болат, бірінші аумақта пайда болат жазық толқын, таратылат z ось бағытында, т. е. шекара манында толқын санымен 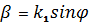 .
.
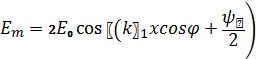
Амплитудалық аумақжазықтық бойынша турақты толқын заны 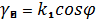 .санымен өзгереді.
.санымен өзгереді.
Осылай, бірінші ортада шекара манында, таратылады жазықтықты бірдей емес толқын. Мұндай толқын бағытталған деп аталады.
6.3. Екінші ретті ортадағы аумақ орташа поляризация ретінде.
Бірінші екінші ретті ортаны қараймйз. Бұл мақсатта қолданамыз мынандай формуланы
Eпрm= yоEпрe-ik2(-xcosθ+zsinθ)
Оны мына түрге келтіруге болады:
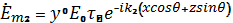 .
.
Физикалық мағынасына (6.1.) байланысты тандаймызтанба «—», жазамыз 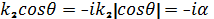 . 2 Зан бойынша Снеллиустын
. 2 Зан бойынша Снеллиустын
 . Осы бойынша:
. Осы бойынша:
 немесе
немесе 
Ең сонғы формула көрсетеді жазықты толқынның аумағын. Таратылатын екінші ортада шекара манында, ал толқын саны β. Бұл толқынның ерекшелігі экспоненционалды өшу аумағы шекараға бағытталған. Бұдан көруге болады, аумаққа екінші орта енгізілмеит және беткі жақтарда болады. Осындай толқынды беткі деп атайды.Тендік толқындардың саны βбағытталған және беткі толқынды көрсетеді олардын фазалық жылдамдығын.
Таратылған беткі толқын характерлі болады арақашықтыққа∆°,азаюы болады толқынның А = 1 Нп (өшу аумағы е рет). Себебі 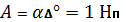 , тосондықтан ∆°=1/α. Толық шағылысқан беткі толқын болмайды.
, тосондықтан ∆°=1/α. Толық шағылысқан беткі толқын болмайды.
7.Аумақтын кескіні, пайда болатын шынайы металлдық тегіс құлау кезіндегі тегіс толқын
7.1.Вектор Ежатыр тегіс түсуде. Электрлік толқын турі
Бағытталған векторПойнтингатүсу толқыны. 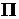 . Мұнадағы түсу толқыны жіне тегіс бірдей фаза, вектор П ға нормальдә болады. (сур. 7.1).
. Мұнадағы түсу толқыны жіне тегіс бірдей фаза, вектор П ға нормальдә болады. (сур. 7.1).
Сур. 7.1.ВекторЕтегіс тұсуде
Әр сызық қозғалған онын қасындағы сызықтын арақашықтығына байланысты, тен болады онын жарты сызық толқынына. Әр сызықтын шегіне байланысты векторЕ өзгермейді өлшемі мен бағыты бойынша. Көршілес сызықта вектор Е бірдей өлшемі мен бағыты бойынша. Вектордын Е бағыты тандалған кезде қандай да болсын сызық фронтында және бағытын біле отырып вектор П-нын , осыған байланысты бірден вектор Н-ді табуға болат.Құлау толқыны, металлдық тегіске жеткен кезде , шағылысады толқын , онын фронты таралады вектор Пойтинг бағытына шағылысқан толқын П.
Сур. 7.2.Электрлік аумақтын күштік сызығы
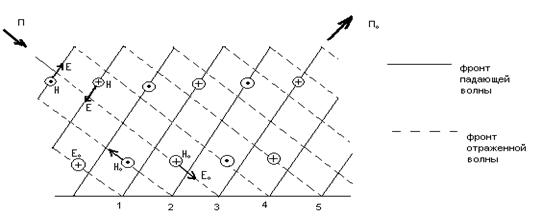
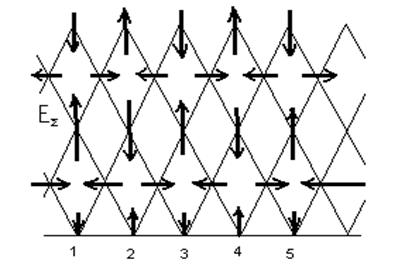
Сур 7.2 көрсетілген түсу векторларының суммасы 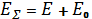 .Сур.7. 3 сетка түрінде көрсетілген.
.Сур.7. 3 сетка түрінде көрсетілген.
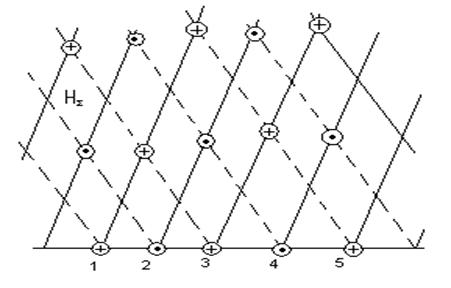
Сур. 7.3.Магнитті аумақтын куштік сызығы
Сур.7.4 көрсетілген ортақ сурет жартыкеністікте куштік сызықты электрлік және магниттік аумақ, құрылымы сур. 7.2 и 7.3. Көрсетілген сурет сәйкес келеді фиксиалдық уақытқа. Олар металлдық тегісіне қарай жылжыйды солдан онға.Осы суреттен табамыз, масштабын көрсетілген суреттін және онын қозғалысының жылдамдығын.
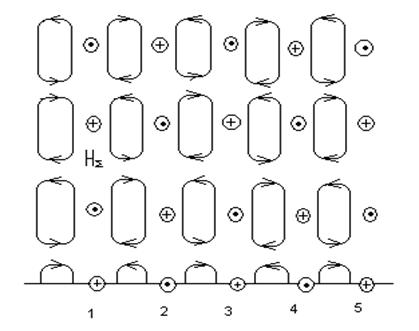
Сур. 7.4.Электрлік және магниттік аумақтын жалпы суреті
сур7.5. көрсетілген жеке қосылған екі фронттын түсу толқынына байланысты екі фронтпен шағылысқан толқын. Суретке байланысты
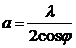 ,
, 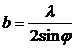 . (7.1.)
. (7.1.)
Осыдан, суреттінмасштабыанықталады сызықты толқынның және тегіс толқынның құлау бурышы металлдық тегіс бойынша.
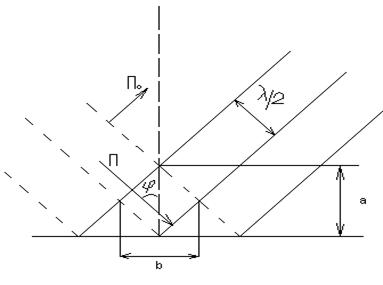
Сур7.5.Құлау толқынының екі фронты шағылысқан толқыны
Сур 7.4. тен көруге болады ,аумақта шекаранын жанындағы магниттік аумағы болад H. Электрлік аумақ Е , векторға сәйкес фазалық жылдамдағы болады.
Мұндай толқынды электрлік типті толқын деп та атайды және оны Е түрінде белгілейд, мұндайда озинде векторлі кернеулі электрлі аумағы және ода жоқ болады векторлық кернеудің магниттік аумақтын құраушысы.
7.2.Вектор Е перпендикулярлі құлау тегісіне. Магнитті типтегі толқын.
Әр жолды қараған кезде екінші ретті аналогты болады біріншіден. Олардын арасындағы айырмашылық бұл жабық болуы сызықтар Е арасы ,екінші ретте олар ауыстырылады Н ссызықтарымен.
Осы суреттердін аумақтарынын масштабтары және көрсетілімдері фазалық жылдамдыққа аналогты болып есептелінеді. Бірінші ретте пайда болады Е түріндегі толқын, ал екінші ретте аумақта Е болмайды онын құраушысы, онын векторынын бағытынын фазалық жылдамдығына тен болмайды, перпендикулярлы болады онын таралуына.
Сызықты құраушысында болады аумақты H. Мұндай толқынды атайды, магнитті типтегі толқын деп және де оны Н әрпімен белгілейді.Жасалынған талдау бойынша , көрсетілді шектеулі таралуды электромагниттік аумақта. Осы бойынша электромагниттік аумақты екі жақтан шектеп, оны параллельді етіп, бірінші металдық тегісті екіншіге орналастыруды қарастырамыз.
7.3. Екі тегістік толқын
Орналастырамыз жоқарыдағы бірінші металлдық тегісті екінші шексіз тегіске идеалды металл арқылы, осылай біз толық суретті бұзып алмаймыз.Сол үшін екінші тегісті орналастыру керек 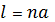 арақашықтықта, мында n=1,2,3,… - толық саннын жолағы. Осыдан Е тура келеді тегіс металлға, ал аумақ H – тангенциальді болады. Шекаралық шарт бойынша , суреттегі аумақтын арақашықтықтығын екі тегіс арасында бірінші тегіс кезінде сияқты сақтау болады.
арақашықтықта, мында n=1,2,3,… - толық саннын жолағы. Осыдан Е тура келеді тегіс металлға, ал аумақ H – тангенциальді болады. Шекаралық шарт бойынша , суреттегі аумақтын арақашықтықтығын екі тегіс арасында бірінші тегіс кезінде сияқты сақтау болады.
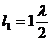 .
.
Минимальное расстояние, при котором возможно существование волны с n=2,
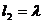 .
.
При 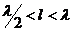 (7.3)
(7.3)
Бейнеде n=1аумағын және Е толқын түрі 7.6-суретте келтірілген. Толқын ұқсас бағытқа перпендикуляр жазықтықтар бойының аумағымен бiр өзгермелi нұсқасымен ие болады және E1 толқын түрiндегi деп аталады. Бейне n=2 аумағын және H2 толқын түрі көрсетілген.
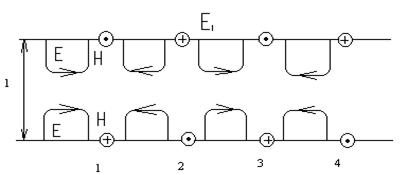
7.6-сурет. Бейне аумағының толқын түрі Е

7.7-сурет. Бейне аумағының толқын түрі H
Жазықтықтар арасындағы қашықтықты (7.1 ) есептеуi:
 (7.2)
(7.2)
Өлшем бірлігі  бұрыштық түсуімен φ байланысты. Мысалы, егер толқын жоғары түрiндегi талап етiлсе, онда 2n есе бұрыш φ өзгермейді, себебі оның пайда болу қашықтығы
бұрыштық түсуімен φ байланысты. Мысалы, егер толқын жоғары түрiндегi талап етiлсе, онда 2n есе бұрыш φ өзгермейді, себебі оның пайда болу қашықтығы  екі рет үлкейтілуі керек. Минималды қашықтық толқынның болу себебі n=1болғанда:
екі рет үлкейтілуі керек. Минималды қашықтық толқынның болу себебі n=1болғанда:
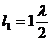 .
.
Минималды қашықтық толқынның болу себебі n=2 болғанда,
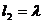 .
.
Бұдан 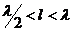 (7.3)
(7.3)
бұл шарт n=1 толқынның даралығын білдіреді. Барлық толқындар үлкен индекстермен екi жазықтықтардың арасында тарата алмайды. Бұл қашықтықта 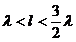 толқын n=2 тең болғанда пайда болады және n=3 тең болғанда толқын пайда болмайды. Дегенмен бiр мезгiлде толқын n=1 бола алады және негізгі деп атаймыз. Қорыта келгенде, жазықтықтар арасындағы қашықтықтың жолымен тиiстi таңдауы толқынның даралығының шарты негiзгi түрiндегi қамтамасыз етiлуге болады және толқындарды даралықтың шарты жоғарғы түрiндегi қамтамасыз етiлуге болмайды. Екiншi жазықтықты енгiзу электромагниттiк кеңiстiкте аса шектеуге тағы рұқсат еттi. Екi шексiз жазықтықтардың жүйесi физикалық түрде шынайы емес. Әрі қарай шынайы арналардың жүйесі мен толқындары қарастырылады.
толқын n=2 тең болғанда пайда болады және n=3 тең болғанда толқын пайда болмайды. Дегенмен бiр мезгiлде толқын n=1 бола алады және негізгі деп атаймыз. Қорыта келгенде, жазықтықтар арасындағы қашықтықтың жолымен тиiстi таңдауы толқынның даралығының шарты негiзгi түрiндегi қамтамасыз етiлуге болады және толқындарды даралықтың шарты жоғарғы түрiндегi қамтамасыз етiлуге болмайды. Екiншi жазықтықты енгiзу электромагниттiк кеңiстiкте аса шектеуге тағы рұқсат еттi. Екi шексiз жазықтықтардың жүйесi физикалық түрде шынайы емес. Әрі қарай шынайы арналардың жүйесі мен толқындары қарастырылады.
Бастапқы формуланы (7.2)-ші формуладан көруге болады, яғни 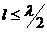 екіжазықтықты толқында толқынның Е және Н түрі болмауы мүмкін.
екіжазықтықты толқында толқынның Е және Н түрі болмауы мүмкін.
Дегенмен, егер магнитті алаңының күш сызықтары жазықтық тангенстің қатынасына байланысты, ал күш сызықтары электрлік алаңына перпендикуляр, 7.8-суретте көрсетілген, толқынның болуы Пойтингінің векторы толқын арнасына жағалай бағытталған. Толқын сол сияқты бойлық құрайтын электрге ие болмайды және магнитті алаңы толқын түрі Т деп аталады. Себебі мұндай толқында Пойтингтің векторы ось бойынша таратылады, толқынның фазалық жылдамдығы Т жарық жылдамдығына тең және толқынды толықтырады. Бұрыштың түсуі
φ мұндай толқын 90°-қа тең болады.
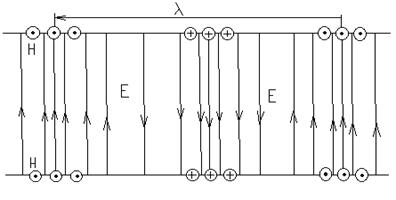
7. 8-сурет. Өзара орналасқан векторлар Е және Н
8. Бағыттайтын жүйелер және электрмагниттiк толқынның бағыты
8.1. Бағыттайтын жүйелер
Толқын бағытының айырмашылығы кеңістікте кеңінен таралуы тек бағытталған элементтерде пайда болуы мүмкін. Бағыттайтын элементтер жиынтығын бағыттайтын жүйелер құрады. Бағыттайтын жүйелерді сонымен қатар қуат беру тораптары деп те атайды.
Барлық беру торабын екi үлкен сыныптарға бөлуге болады: беру торабы ашылған түрiндегi және беру торабы жабық түрiндегi. Беру торабының жабық түрінде барлық қуат бір кеңістікте бағытталған және экранның сырты металмен қабатталған. Беру торабы ашық түрiндегi ЭМП тура айтқанда, кеңістікте кеңінен таралған. Дегенмен, ашық жол туралы әдетте атқарылған, ЭМП басым түскен қуаттың бір бөлігі желіден тікелей жақындықта шоғырланған.
8.2 Толқындарды бағыттауды жіктеу
Толқынның бағыты бөлінеді: көлденең, электрлік, магниттік және араласқан. Көлденең және толқын түрі Т толқын деп аталады,таралуы бағытында қуаттың кеңінен бағытталуы электр құраушының және магнит аумағының векторларының болмауынан. 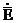 және
және  векторлары кеңінен жазықтықта перпендикуляр бағытталған. Электрлік немесе толқын түрі Е толқын деп аталады, басқа электр өрісінің векторларында көлденең құрайтын бойлық ие болады. Магнитті алаңның бойлық векторы нөлге тең. Магниттік және толқын түрі Н толқын деп аталады, басқа магнит аумағының векторы көлденең құрайтын бойлық толқын дейді. Электр өрісінің бойлық құраушысы нөлге тең. Араласқан (гибридті) толқын деп атайды, басқа электрлік және магниттік аумақтың векторларын көлденең құрайды.
векторлары кеңінен жазықтықта перпендикуляр бағытталған. Электрлік немесе толқын түрі Е толқын деп аталады, басқа электр өрісінің векторларында көлденең құрайтын бойлық ие болады. Магнитті алаңның бойлық векторы нөлге тең. Магниттік және толқын түрі Н толқын деп аталады, басқа магнит аумағының векторы көлденең құрайтын бойлық толқын дейді. Электр өрісінің бойлық құраушысы нөлге тең. Араласқан (гибридті) толқын деп атайды, басқа электрлік және магниттік аумақтың векторларын көлденең құрайды.
8.3 Бойлық және үздіксіз бағыттайтын жүйеде көлденең құрайтын байланыс арасы
Туындының шексіз ұзындығының бағытталған жүйесі Z осіне жағалай бағытталуын қарастырамыз. Осыған орай, бағытталған жүйенің қателігін енгізеді және ол біртекті, сонымен:
· түпкі қиманың пішіні Z-ке бағынышты болмайды;
· ЭМП таратқан ортаның параметрлері және шекаралық шарты Z-ке бағынышты болмайды.
Шеткері көздері 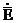 Гельмгольцтың біртекті теңдеуімен қанағаттануы керек:
Гельмгольцтың біртекті теңдеуімен қанағаттануы керек:
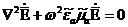
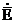 және
және  координаталарының тәуелділігі Z -ке көбейтіліп
координаталарының тәуелділігі Z -ке көбейтіліп 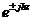 суреттеледі, біртекті Гельмгольц теңдеуінде
суреттеледі, біртекті Гельмгольц теңдеуінде 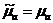 және
және 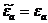 алғанда:
алғанда:
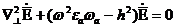 (8.1)
(8.1)
Мағынасы
 (8.2)
(8.2)
мұнда g – толқын саны.
(8.1) теңдеуде, эквивалентті үш скалярлық теңдеу бойлық үшін және екі көлденеңді құрайды. Көлденең құрайтыны арқылы бойлық ара қатынастардың көмегiмен бiлуге болады және бұдан Максвеллдің дифференциалдық теңдеуі шығады.
Максвеллдің біртекті теңдеуін түрлендіреміз:
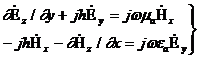 (8.3)
(8.3)
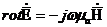
Шешімін таба отырып, (8.3) қатысты 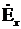 аламыз:
аламыз:
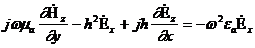
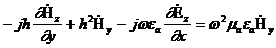
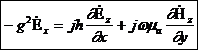 (8.4)
(8.4)
Сонымен ұқсастығын (8.4) 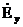 аламыз:
аламыз:
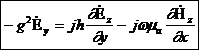 (8.5)
(8.5)
Теңдеу жүйесінің (8.4)-(8.5)көлденең және бойлық құрайтын аумақта декарттық жүйесімен байланысты. Ерiктi координаттар жүйесiне байланысты теңдеулердi векторлық пiшiнге өтемiз. Векторды енгіземіз  . Осы теңдеудің орнына қойып
. Осы теңдеудің орнына қойып 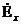 және
және 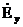 осылардан мәнін (8.4) - (8.5) аламыз:
осылардан мәнін (8.4) - (8.5) аламыз:
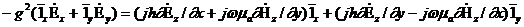
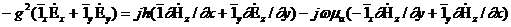 .
.
Осының мағынасы 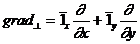
есептей отыра, 
аламыз 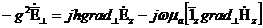 (8.6)
(8.6)
Ұсас теңдіктер шығады.
Қорыта келгенде, толық құрылымның аумағын табуы үшiн екi дифференциалдық теңдеудi шекаралық шарттармен есептеуімен шешiлу керек:
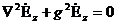 (8.7)
(8.7)
және теңдеудің теңдігі (8.6) көлденең құрауын анықтайды.
8.4. Сындық жиілігі. Сындық жиілігінің толқыны

h, нақты мәні болса, онда
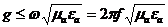 (8.8)
(8.8)
жалған мәні, онда
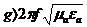 (8.9)
(8.9)
Біріншіден фаза жағдайында Z сызықтық заң бойынша, толқындардың кеңінен таралуы фазаның тұрақта жылдамдықпен ось бойынша жағалай өзгереді. Екіншіден Z осімен жағалай жүруі фазаның тұрақты жағдайда қалып отырады, ал амплитуда жағалай бағытталған жүйені қуатты тасымалдау жоқтығынан экспонента бойымен кемиді.
Жиілік шартының анықталуы
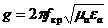 (8.10)
(8.10)
сындық деп атайды.
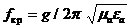 (8.11)
(8.11)
Толқын ұзындығы тиiстi мына сындық жиiлiкке тең:
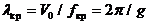 (8.12)
(8.12)
Онда 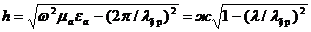 (8.13)
(8.13)
где 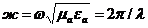 - толқын саны,
- толқын саны,
а 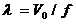 - толқын ұзындығы параметр ортасында
- толқын ұзындығы параметр ортасында 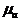 және
және 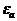 тең.
тең.
Сәйкесінше (8.9) кеңінен таралған толқындардың бағытталу жүйесі жиіліктің сындық орнын көтереді 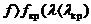 .
.
Толқын ұзындығы  көлденең қималарының арасындағы минималды қашықтықты бағыттайтын жүйеде толқын ұзындығымен және Z координата осінде фаза бойымен 2p-ге жылжып отырады. Координата Z құрайтын аумағының тәуелділігі көрсетілген:
көлденең қималарының арасындағы минималды қашықтықты бағыттайтын жүйеде толқын ұзындығымен және Z координата осінде фаза бойымен 2p-ге жылжып отырады. Координата Z құрайтын аумағының тәуелділігі көрсетілген: 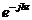 , яғни
, яғни
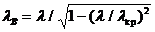 (8.14)
(8.14)
9 Көлденең электромагниттік толқындар
9.1 (Еz =0 , Нz =0) Толқынның сындық ұзындығы
Арақатынасында (8.7) и (8.8) Еz = Нz =0 , аламыз
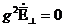 ,
, 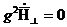 (9.1)
(9.1)
осы мәнді қанағаттандырады 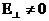 и
и 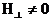 ,
,
тек қана 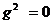 (9.2)
(9.2)
Сәйкесінше (8.11) , (8.12) осы мәндерде g-ді алады және 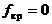 . Сондықтан, осы бағытталған жүйеде, мұндағы Т кеңінен тарлған толқын әр түрлі жиілікте болады.
. Сондықтан, осы бағытталған жүйеде, мұндағы Т кеңінен тарлған толқын әр түрлі жиілікте болады.
9.2 Тұрақты таралуы.Толқынның фазалық жылдамдығы
 ,
, 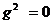 Þ
Þ 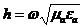 (9.3)
(9.3)
 (9.4)
(9.4)
Аумақтың потенциалдық сипаттамасы.
Бұл теңдеуде 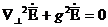

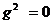
Еz = Нz =0
аламыз: 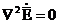 (9.5)
(9.5)

(9.5) теңдеуде екі өлшемді Лаплас теңдеулер болады. Лаплас теңдеуі қанағаттанарлық ықтимал болып көрінеді. (9.5) теңдеудің шешімі екенін және кейбір функцияның градиенті болуы мүмкіндігін көрсетеді. Мысалы:
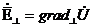 (9.6)
(9.6)
мұнда  -скаляр потенциалы, сонымен қатар Лаплас теңдеуін қанағаттандырады:
-скаляр потенциалы, сонымен қатар Лаплас теңдеуін қанағаттандырады:
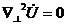 .
.
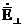 векторы бір-бірінен айырылып тұрады. Мұнда (8. 6) , Еz = Нz =0,
векторы бір-бірінен айырылып тұрады. Мұнда (8. 6) , Еz = Нz =0,
қатынасына келсек:
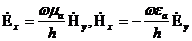 ,
,
векторлық түрде жазуға болады:
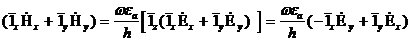
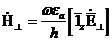 (9.7)
(9.7)
осыған орай, векторлары 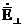 және
және  толқыны Т бір-бірене перпендикуляр.
толқыны Т бір-бірене перпендикуляр.
9.3 Кедергілердің сипаттамасы
(9.3) және (9.6) формуланы қоя отырып, мынаны аламыз
 (9.8)
(9.8)
мұндағы 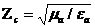 - кедергілер толқынының сипаттамасы Т.
- кедергілер толқынының сипаттамасы Т.
(9,8) теңдеуде жиілік кірмейді. Осыдан қорытынды алсақ, толқын құрылымы Т жиілікке тәуелді емес. Желiні көлденең қимада Т толқынды электр өрiсiсiнiң үлестiруi жеке алғанда сол жүйедеге статикалық электр өрiсiсiнiң үлестiруiмен үйлеседi. Ұқсас сәйкестікте және магниттік өрістің арақатынасында болады. Бұл суретте электрлік және магниттік өрістің көлденең қимасы екі өткізгішті және коаксиальды желінің құрылымдық сұлбасы көрсетілген.
Осы сияқты толқынның құрылымдық сұлбасы Т әр түрлі жиілікте болады. Толқын Т кеңінен таралған бағытталған жүйенің қуатына берілуі мүмкін.
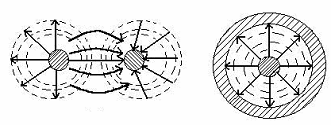 |
9.1-сурет. Электрлік және магнит өрісінің көлденең қимасының екі өткізгішті және коаксиальды желінің құрылымдық сұлбасы.
Тұрақты тоқта мұндай бағытталған жүйе кемінде екі немесе оданда көп сымдардан тұрады.
Көлденең жазықтықта Т толқынында, өзгерiссiз қалмаған статикалық жағдай болғанын кешiккенiнде емес, синусоида заңы бойымен өз амплитудалар үздiксiз өзгерткенiнде, Z координата бойынша тәуелді.
ЭМП-ның өткізгіштерiн мiнсiз өткiзу қабiлетi жанындағы металға кiредi. Щукин - Леонтовичтың шекаралық шарттарымен сәйкес нөлден бастап электрлік өрісінде параллель жалғанған Z осі, Т толқынның болуы мүмкін емес. Дегенмен толқынның металл құрылымы биiк өткiзу қабiлетiнiң жанында толқын аумағының Т құрылымнан аз ерекшеленедi және жағдайын өзгелiк көпшiлiгiнде елемеуге болады.
10 Электрлік толқыны
10.1 Байланыс аумағының арасында ( 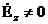 және
және 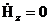 )
)
Осы қатынастан:
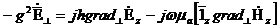 ,
,
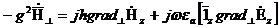 ,
,
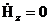 , аламыз:
, аламыз: 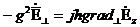 , (10.1)
, (10.1)
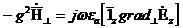 , (10.2)
, (10.2)
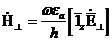 . (10.3)
. (10.3)
Сонымен 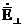 және
және  векторлары оның Е толқынына перпендикуляр.
векторлары оның Е толқынына перпендикуляр.
10.2 Кедергінің сипаттамасы
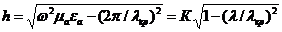 . (*)
. (*)
Сонымен (10.3) кедергінің сипаттамасын былай жазуға болады:
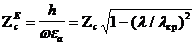 , (10.4)
, (10.4)
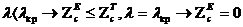 .
.
бұл l > lкр ® 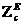 - жалған мәні. Бұл электр векторының құраушысы көлденең қимасы және магниттi өрісі 90 градустарға фаза бойымен жылжытылған. Пойнтингтiң векторы бұл ретте таза жалған мағыналар қабылдағаны анық, және айнымалы белсендi қуатты тасымалдауды болмайды. Сондықтан экспоненталық сызық бойымен кемуі l > lкр энергия шығындары немесе реактивті ЭМП сызығының сипаттамасы.
- жалған мәні. Бұл электр векторының құраушысы көлденең қимасы және магниттi өрісі 90 градустарға фаза бойымен жылжытылған. Пойнтингтiң векторы бұл ретте таза жалған мағыналар қабылдағаны анық, және айнымалы белсендi қуатты тасымалдауды болмайды. Сондықтан экспоненталық сызық бойымен кемуі l > lкр энергия шығындары немесе реактивті ЭМП сызығының сипаттамасы.
10.3 Фазалық жылдамдық. Дисперсия
 (8.5) , Vф > V0 ; l = lкр ® Vф = µ.
(8.5) , Vф > V0 ; l = lкр ® Vф = µ.

Фазалық жылдамдықтың тәуелділігі Vф жиіліктің дисперсиясы деп аталады, ал толқын дисперсиясының алатын орнын дисперсияланған деп атауға болады.
11 Бағытталған жүйе
11.1 Тік бұрышты толқын арнасы. Электрлік толқын ( 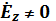 и
и 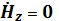 ).
).

Рис.11.1 Прямоугольный волновод
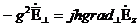 ,
,
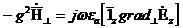 .
.
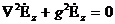
имеет в декартовой системе координат вид:
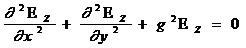 , (11.1)
, (11.1)
Решение (11.1) 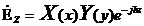 . (11.2)
. (11.2)
где Х(Х) - функция только Х , Y(y) - функция только Y.
(11.2)® (11.1) Þ 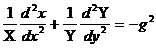 (11.3)
(11.3)
Выполнение (11.3) при произвольных значениях Х и Y возможно, если
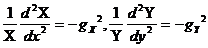 , (11.4)
, (11.4)
где 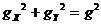 , (11.5)
, (11.5)
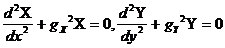 . (11.6)
. (11.6)
Решение (11.6) имеет вид:
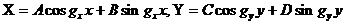 (11.7)
(11.7)
(11.7)® (11.2) Þ 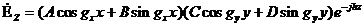 (11.8).
(11.8).
Так как стенки волновода предполагаются идеально проводящими, то, применяя граничное условие 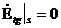 :
:  при х=0, х=a и при y=0, y=b
при х=0, х=a и при y=0, y=b


это возможно, если:
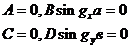
для этого необходимо : 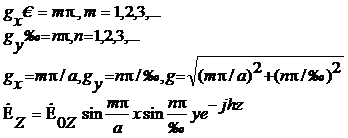 (11.9)
(11.9)
где 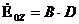 и имеет смысл амплитуды продольной составляющей
и имеет смысл амплитуды продольной составляющей 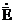 .
.
(11.1)и (11.2) в декартовой системе координат имеют вид:
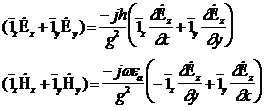
Подставляя (11.9) получим:
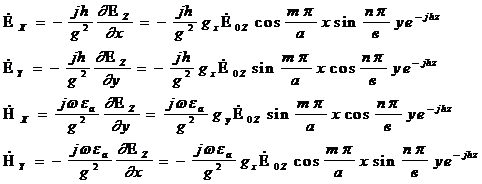 (11.10)
(11.10)
Как следует из (11.9), (11.10) структура поля волн типа Е в плоскости поперечного сечения соответствуют структуре стоячих волн, причем m равно числу полуволн, укладывающихся вдоль стенки длиной а, и n - число полуволн, укладывающихся вдоль стенки длиной b. Каждой паре чисел m и n соответствует определенная структура ЭМП, обозначаемая Еmn.
Отметим, что структуру волны Еz1 можно получить повторением структуры волны Е11 вдоль соответствующей координаты.
 ,
,
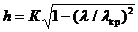 ,
,
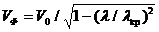
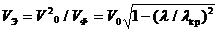 ,
,
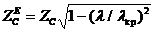 .
.
Низшим типом среди волн Еmn , обладающей наибольшей lкр, является волна Е11. Волны Еmn с различной структурой поля, которым соответствуют одинаковые значения g, имеющие равные коэффициенты распространения, фазовые скорости и скорости распространения энергии, называются вырожденными.
11.2. Магнитные волны ( 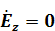 и
и 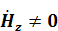 ).
).
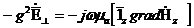 ,
,
 .
.
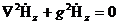
имеет в декартовой системе координат вид:
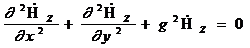 , (11.11)
, (11.11)
 . (11.12)
. (11.12)
На поверхности идеально проводящих стенок волновода должно выполнятся граничное условие: 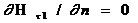 .
.
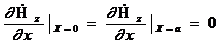 , (11.12)
, (11.12)
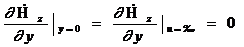 . (11.13)
. (11.13)
Подставляя (11.13), (11.14) в (11.12), приходим к соотношениям
 (11.15)
(11.15)
Как следует из (11.15), у волн Н, как и у волн Е,
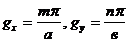 ,
,
т.е. волны Н и Е с равными индексами являются вырожденными.
Подставляя в (11.12) (11.15) и значения 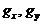 , получим:
, получим:
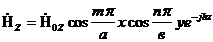 . (11.16)
. (11.16)
где Н0Z - =АС - амплитуда продольной составляющей магнитного поля.
Соотношения (11.1) , (11.2) в декартовой системе координат имеет вид:
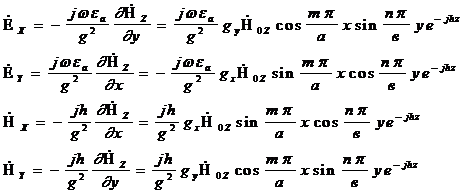 (11.17)
(11.17)
Как следует из равенств (11.16), (11.17), у волн Н, в отличие от волн Е, обращение в нуль одного из индексов (m или n) не влечет за собой обращения в нуль всех составляющих поля. Поэтому, если полагать а>b, то низшим типом волн Н является волна Н10.
 ,
,
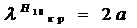
Поскольку 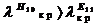 , то волна Н10 является низшим типом волны не только среди волн Н, но и среди всех возможных типов волн в прямоугольном волноводе. Это означает, что при l>2а передача энергии по прямоугольному волноводу невозможна.
, то волна Н10 является низшим типом волны не только среди волн Н, но и среди всех возможных типов волн в прямоугольном волноводе. Это означает, что при l>2а передача энергии по прямоугольному волноводу невозможна. 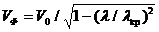 ,
,
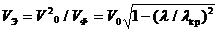 ,
,
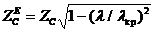 .
.
11.3. Волна Н10
Волна Н10 имеет наибольшую критическую длину волны. Поэтому на заданной частоте размеры поперечного сечения волновода, при которых возможна передача энергии по волноводу, наименьшие для этой волны.
Полагая в (11.16), (11.17) m=1 и n=0 , получим:
 , (11.18)
, (11.18)
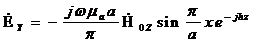 , (11.19)
, (11.19)
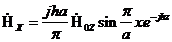 , (11.20)
, (11.20)
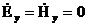 . (11.21)
. (11.21)
Остановимся на картине распространения поля волны Н в плоскостях параллельных широкой стенке волновода.
В ЭМП волны Н10, магнитные силовые линии охватывают токи смещения, текущие между широкими стенками параллельно оси у.
Максимальная плотность тока смещения находится в центре замкнутых магнитных силовых линий, где напряженность электрического поля равна нулю
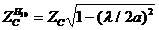 ,
,
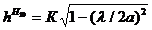 ,
,
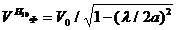 ,
,
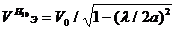 ,
,
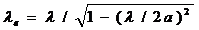 .
.
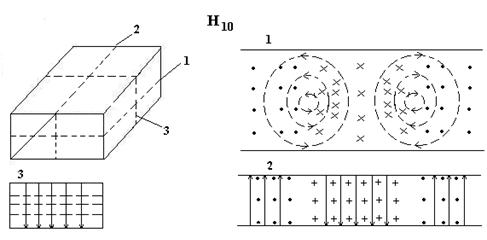
Рис. 11.2.Структура поля волны Н10

Рис.11.3. Диаграмма типов волн прямоугольного волновода
Круглый волновод

Рис.11.4. Круглый волновод
В круглом волноводе возможно существование волн E и H и невозможно распространение волн T.
Электрические волны
При анализе воспользуемся цилиндрической системой координат, совместив ось с продольной осью волновода.
Ур-ние 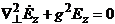 в полярной системе координат примет вид:
в полярной системе координат примет вид: 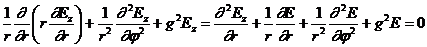 (11.22)
(11.22)
Решение (11.22) 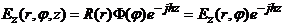 . (11.23)
. (11.23)
Подставив (11.23) в (11.22), умножив обе части на r2, выпполнив дифференцирование и ив полученное уравнение на  , получим
, получим
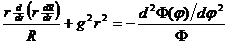 (11.24)
(11.24)
Левая часть (11.24) зависит только от r, правая - только от j. Переменные r и j - независимые. Следовательно (11.24) - равенство двух независимых функций. Это возможно, если каждая из функций равна постоянной. Обозначая постоянную m2, приходим к двум дифференциальным уравнениям:
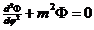 , (11.25)
, (11.25)
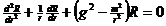 (11.26)
(11.26)
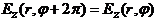 (11.27)
(11.27)
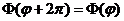 (11.28)
(11.28)
Решение уравнения (11.25) имеет вид
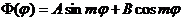 ,
,
где A и B - произвольные постоянные. Условие (11.28) выполняется, если m=0,1,2...
Уравнение (11.26) является уравнением Бесселя. Его решение можно представить в виде
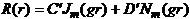 . (11.29)
. (11.29)
где 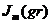 и
и  - функции Бесселя m-го порядка первого и второго рода, а
- функции Бесселя m-го порядка первого и второго рода, а 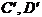 - произвольные постоянные.
- произвольные постоянные.
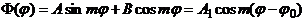 , (11.30)
, (11.30)
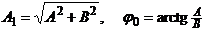 .
.
В отношении (11.30) функция Бесселя второго рода при 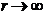 стремится к ¥. Так как напряженность поля в любой точке волновода должна быть ограничена, то необходимо потребовать
стремится к ¥. Так как напряженность поля в любой точке волновода должна быть ограничена, то необходимо потребовать 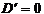 . Тогда
. Тогда
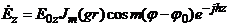 . (11.31)
. (11.31)
где 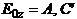 - амплитуда продольной составляющей электрического поля
- амплитуда продольной составляющей электрического поля
учитывая, что 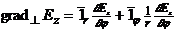 :
:
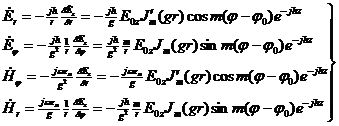 (11.32)
(11.32)
где штрих означает дифференцирование по всему аргументу функции Бесселя.
Согласно граничному условию
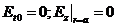 . (11.33)
. (11.33)
Подставляя (11.31) в (11.33), получаем
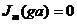 (11.34)
(11.34)
Имеется бесконечно большое число значений аргумента, при которых функция Бесселя равна нулю. Эти значения называются корнями функции Бесселя. Обозначая n-й корень функции Бесселя m-го порядка через  , из (11.34) находим
, из (11.34) находим
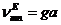 , откуда
, откуда 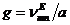 (11.35)
(11.35)
Нумерация Е волн, отличающихся друг от друга по структуре поля в плоскости поперечного сечения волновода, осуществляется в соответствии с порядковым номером корня уравнения (11.34). При этом индекс m соответствует числу целых стоячих волн поля, укладывающихся по окружности волновода, а индекс n характеризует распределение стоячих волн вдоль радиуса волновода.
Несколько первых корней функции Бесселя 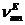 в порядке их возрастания и соответствующие им критические длины волн
в порядке их возрастания и соответствующие им критические длины волн 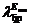 представлены в таблице.
представлены в таблице.
| Тип волны | E01 | E11 | E21 | E | E | E | E | E |

| 2.405 | 3.832 | 5.135 | 5.520 | 6.379 | 7.016 | 7.586 | 8.407 |
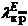
| 2.613 | 1.640 | 1.223 | 1.138 | 0.985 | 0.895 | 0.828 | 0.746 |
Низшим типом среди волн E в круглом волноводе является волна E01.
 ,
,
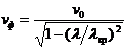 ,
,
 ,
,
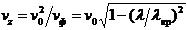 ,
,
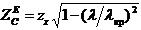 .
.
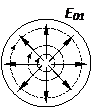

Рис.11.5. Структура поля волны Е01
11.6. Магнитные волны ( 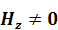 ,
,  )
)
Будем рассуждать аналогично случаю с электрическими волнами
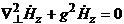
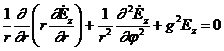
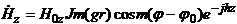
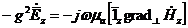
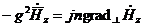
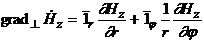
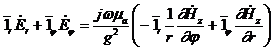
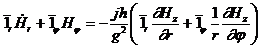
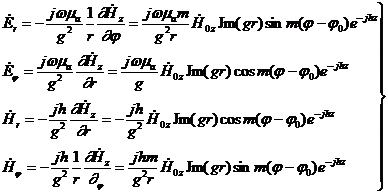 (11.37)
(11.37)
Отметим, что при выполнении Jm(ga)=0 согласно 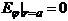
 (11.38)
(11.38)
Несколько первых корней функции Бесселя 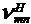 в порядке их возрастания и соответствующие длины волн
в порядке их возрастания и соответствующие длины волн 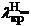 представлены в таблице.
представлены в таблице.
| Тип волны | H11 | H21 | H01 | H31 | H41 | H12 | H51 | H21 | H02 |
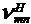
| 1.84 | 3.05 | 3.83 | 4.20 | 5.32 | 5.33 | 6.42 | 6.71 | 7.02 |
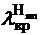
| 3.41 | 2.06 | 1.64 | 1.50 | 1.182 | 1.178 | 0.979 | 0.934 | 0.838 |
Низшим типом среди не только волн H, но и всех волн в круглом волноводе, как следует из сравнения двух таблиц, является волна H11.

Рис.11.6.Структура поля волны Н11
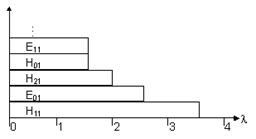
Рис.11.7. Диаграмма типов волн круглого волновода
Коаксиальный волновод
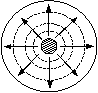

Рис. 11.8 Структура поля коаксиального волновода
Волна T. Волновое сопротивление коаксиальной линии
В коаксиальных линиях возможно существование волн T, E и H.
Так как у волны T 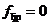 , то эта волна является низшим типом волны в коаксиальной линии.
, то эта волна является низшим типом волны в коаксиальной линии.
Уравнение Лапласа ( 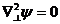 ) в полярной системе координат имеет вид
) в полярной системе координат имеет вид
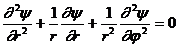 (11.39)
(11.39)
Уравнению (11.39) соответствуют два решения:
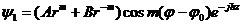 (11.40)
(11.40)
 , (11.41)
, (11.41)
где m - целое число.
На поверхности внутреннего проводника и на внутренней поверхности внешнего проводника, которые полагаются идеально проводящими, касательная составляющая электрического поля должна обращаться в нуль
 (11.42)
(11.42)
Следовательно, решение (11.40) при  и
и  не удовлетворяет граничному условию (11.42) и его следует отбросить. Для второго решения
не удовлетворяет граничному условию (11.42) и его следует отбросить. Для второго решения

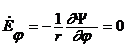 ,
,
т.е. граничное условие (11.42) выполняется тождественно при произвольном значении константы D и функция Y2 является искомым решением.
Подставляя в ( 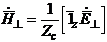 ) функцию Y2, находим
) функцию Y2, находим
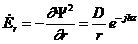 , (11.43)
, (11.43)
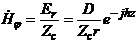 (11.44)
(11.44)
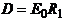 , где E0 - модуль напряженности эле критического поля у поверхности внутреннего проводника.
, где E0 - модуль напряженности эле критического поля у поверхности внутреннего проводника.
Структура поля, соответствующая (11.43), (11.44) изображена на рис.11.8

Разность потенциалов между центральным и внешним проводниками равна
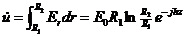 (11.45)
(11.45)
Ток, текущий по поверхности центрального проводника и по внутренней поверхности внешнего проводника, равен
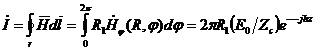 (11.46)
(11.46)
Отношение напряжения u к току I в режиме бегущей волны называется волновым сопротивлением коаксиальной линии
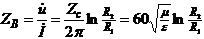 (11.47)
(11.47)
Дата добавления: 2018-02-28; просмотров: 928; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!