Формулы размещения, сочетания, перестановки
Основные понятия комбинаторики: правила сложения и умножения, формулы размещений, сочетаний, перестановок
Понятие о комбинаторике
Комбинаторика – ветвь математики, изучающая различные комбинации и перестановки объектов. Возникла комбинаторика в 17 веке. Развивалась наука в 18 веке благодаря научным трудам итальянских ученых Кардано, Тартальи, Галилея; французских математиков Паскаля и Ферма; немецких ученых Лейбница и Эйлера. Впервые название науки «комбинаторика» ввел Леонард Эйлер.
Первоначально комбинаторика возникла на основе азартных игр. К таким играм относятся: карты, кости, шашки, шахматы, нарды. Выигрывает в них тот, кто лучше изучил выигрышные комбинации, просчитал все возможные исходы на несколько шагов вперед и избежал проигрыша.
Не только игры давали пищу для комбинаторных размышлений. Разведчики, дипломаты, стремясь к тайне переписки, изобретали различные шифры и коды.
В современном обществе с развитием ЭВМ комбинаторика добилась новых успехов. Она применяется довольно широко: в теории случайных процессов; в статистике; в математическом программировании; в вычислительной математике; в военном искусстве; в управлении и т.д.
С помощью комбинаторики, например, была решена проблема «четырех красок». Любую географическую карту можно раскрасить в четыре цвета так, что никакие две страны, имеющие общие границы, не будут окрашены в один цвет.
|
|
|
Правила умножения и сложения
Установим два важных правила, которые часто применяются при решении комбинаторных задач. Для этого рассмотрим решение следующей задачи.
Пример 1.В группе студентов 30 человек. Необходимо выбрать старосту и профорга. Сколькими способами можно это сделать?
Решение. Старостой может быть выбран любой из 30 учащихся, т.е. существует 30 способов выбора старосты. После того как староста уже выбран, профоргом можно выбрать любого из оставшихся 29 учащихся. Таким образом, одному способу выбора старосты соответствует 29 способов выбора профорга. Следовательно, общее число способов выбора старосты и профорга равно 30*29=870.
Рассуждения, которые были проведены при решении предыдущих задач, подтверждают справедливость следующего простого утверждения.
Правило умножения.Пусть требуется выполнить одно за другим какие-то k действий. Если первое действие можно выполнить n1 способами, второе действие – n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nк способами, то все к действий вместе могут бать выполнены n1∙ n2∙ n3∙…∙ nк способами.
Это правило дает удобный универсальный метод решения многих комбинаторных задач.
|
|
|
Пример 2.Четыре мальчика и четыре девочки садятся на 8 расположенных подряд стульев, причем мальчики садятся на места с четными номерами, а девочки - на места с нечетными номерами. Сколькими способами можно это сделать?
Первый мальчик может сесть на любое из четырех четных мест, второй – на любое из оставшихся трёх мест, третий – на любое из оставшихся двух мест. Последнему мальчику предоставляется всего одна возможность. Согласно правилу умножения, мальчики могут занять четыре места 4*2*3*1=24 способами. Столько же возможностей имеют и девочки. Таким образом, согласно правилу умножения, мальчики и девочки могут занять все стулья 24*24=576 способами.
Пример 3.Нефтекамский завод «Искож» выпускает трикотажные изделия. На складеимеется 20 изделий 1-го сорта и 30 изделий 2-го сорта. Необходимо выбрать два изделия одного сорта. Сколько способов выбора двух изделий возможно в данной ситуации, если учитывается порядок выбора изделий?
Условимся первым действием считать выбор изделий 1-го сорта, вторым – выбор изделий 2-го сорта. По правилу умножения два изделия 1-го сорта можно выбрать 20*19=380 способами. Аналогично, два изделия 2-го сорта можно выбрать 30*29=870 способами. Согласно условию задачи следует выбрать два изделия одного сорта, не важно какого. Это могут быть либо изделия 1-го сорта, либо изделия 2-го сорта. Таким образом, должно быть выполнено либо первое действие, либо второе, но не первое действие, а затем второе. Эти действия не могут быть выполнены одновременно, поскольку они взаимно исключают друг друга. Поэтому общее число способов выбора изделий одного сорта равно 380+870=1250.
|
|
|
Соображения, которые были приведены при решении последней задачи, позволяют сформулировать правило сложения.
Правило сложения.Если два действия взаимно исключают друг друга, причем одно из них можно выполнить m способами, а другое – n способами, то выполнить одно любое из этих действий можно n+m способами.
Это правило легко распространить на любое конечное число действий.
Формулы размещения, сочетания, перестановки
Комбинаторика занимается вопросами о том, сколько комбинаций определенного типа можно составить из данных элементов. Группы, составленные из каких-либо элементов, называются соединениями.
Пусть имеется некоторое множество, содержащее конечное число членов. Например, множество учебных групп в колледже, множество книг на полке, множество населенных пунктов в данной области или, например, множество целых положительных чисел, меньших 10, и т.д. Все элементы такого множества можно пронумеровать, т.е. каждому элементу множества можно поставить в соответствие одно из чисел: 1, 2, 3, 4, …,n; в результате получается некоторая последовательность элементов данного множества, которые обычно записывают в виде а1, а2, а2, …, ап. Такие “ занумерованные” множества будем называть упорядоченными. Таким образом, упорядоченное множество представим в виде некоторой последовательности, что будет использовано в дальнейшем. Очевидно, если в упорядоченном множестве поменять местами хотя бы два его элемента, то получим новое упорядоченное множество, которому будет соответствовать новая последовательность элементов данного множества. Введем определение факториала.
|
|
|
Определение.Произведение всех натуральных чисел от 1 до п включительно называют n − факториалом и пишутn! = 1∙2∙3∙4∙…∙(n – 1)∙n
Определение. Размещением из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения.
Пример 4. Пусть имеется множество, содержащее четыре буквы:{A, B, С; Д}. Таких размещений 12: AB, AC, AD, BC, BD, CD, BA, CA, DA, CB, DB, DC.
Заметим, что размещения отличаются порядком входящих в них элементов и их составом. Размещения АВ и ВА содержат одинаковые буквы, но порядок их расположения различен. Поэтому эти размещения считаются разными.
Пример 5.Следующие последовательности цифр являются размещениями по 4 элемента из 10 элементов множества:{0,1,2,3,4,5,6,7,8,9,}: 3021, 4590, 8612, 7485, 1234.
В последнем примере не выписаны все возможные размещения, так как таких размещений более 5000.
На практике чаще представляет интерес количество размещений, а не их конкретный вид. Число размещений из nэлементов по mбудем обозначать символом Атп,где m<nилиm=n.
Теорема.Число размещений из n элементов по m равно 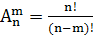
Пример 6.Сколько можно записать четырехзначных чисел, используя без повторения все десять цифр?
Так как в любом числе важную роль играет порядок входящих в него цифр, то для ответа на поставленный вопрос, очевидно, следует определить число размещений из 10 цифр по 4:
А410 = 10!/6!=7*8*9*10=5040.
Однако все последовательности из 4 цифр представляют собой четырёхзначное число, поскольку среди них есть и такие, у которых на 1-м месте находится 0. Найдем число таких последовательностей. Так как у рассматриваемых последовательностей на 1-м месте уже стоит 0, то следует выбрать ещё 3 цифры из оставшихся 9. Найдем число размещений из 9 по 3: А39=9!/6!=7*8*9=504. Таким образом, искомое число четырехзначных чисел равно разности А410 - А39 =5040-504=4536.
Рассмотрим теперь отдельно случай, когда m=n. Соответствующие этому случаю размещения называются перестановками.
Перестановками из n элементов называются такие соединения из всех n элементов которые отличаются друг от друга порядком расположения элементов.
Пример 7.Пусть имеются числа 3, 5, 7. Этому множеству чисел соответствует 6 перестановок: 357, 375, 537, 573, 753,735.
Пример 8.Слова “барк” и “краб” образованы в результате перестановки букв, составляющих слово “брак”. Число таких перестановок равно 24, так как
А44 = 4!/0!=4!=1*2*3*4=24.
Отметим, что перестановки состоят из одних и тех же элементов, но отличающихся между собой порядком. Число перестановок nразличных элементов будем обозначать символом Рп .
Теорема.Число перестановок n различных элементов равно n!, т.е.  =n!
=n!
Так как перестановки являются частным случаем размещений, то при n=mполучаем
 =
= 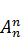 =n!/0!=n!
=n!/0!=n!
Пример 9.Сколькими способами можно расставить 9 различных книг на полке, чтобы определенные четыре книги стояли рядом?
Способ 1. Будем считать выделенные книги за одну книгу. Тогда для шести книг существует Р6=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой Р4=4!=24 способами. По правилу умножения имеем Р6 ∙ Р4 =720∙24=17 280.
Способ 2.Возможны следующие случаи: первая из четырёх книг стоит на 1-м месте, тогда четвёртая стоит на 4-м месте; первая книга стоит на 2-м месте, а четвертая стоит на 5-м месте, первая стоит на 6-м месте, тогда четвертая стоит на последнем, 9-м месте. Число таких случаев равно шести. Сами книги могут быть переставлены Р4=4!=24 способами. Значит, по правилу умножения выделенные четыре книги можно расставить 6∙Р4=144 способами. Оставшиеся 5 книг можно переставить Р5=5!=120 способами. Воспользовавшись снова правилом умножения, приходим к тому же результату, который был получен при первом способе решения: Р4∙6∙Р5 = Р6 ∙ Р4 = 17 280.
Если два различных размещения состоят из одинаковых элементов некоторого множества, то они обязательно отличаются порядком входящих в них элементов. Иногда возникает необходимость не учитывать порядок элементов, входящих в размещение. В этом случае все m!размещений, которые состоят из одних и тех же элементов, считаются неразличимыми.
Предположим, что из чисел 3, 5, 7 необходимо составить различные произведения двух чисел. Таких произведений только три: 3∙5=15, 3∙7=21,5∙7=35. Это объясняется тем, что произведения вида 3∙5 и 5∙3 совпадают, так как порядок сомножителей, входящих в произведение, не учитывается. Если требуется из указанных цифр составить двузначные числа, то таких чисел уже шесть. Запишем эти числа: 35, 53, 37, 73, 57, 75. Как видно, здесь уже пришлось учитывать порядок цифр.
При выборе делегации в составе 3 человек из 30 учащихся не надо учитывать порядок выбранных делегатов, так как все члены делегации равноправны. Однако, выбирая физорга, старосту, профорга из тех же учащихся, порядок уже приходится учитывать. Каждый конкретный результат выбора из 30 учащихся делегации в составе 3 человек – это сочетание из 30 по 3 в отличие от размещения из 3 по 3.
Сочетаниями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.
Пример 10.Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Из смысла задачи следует, что порядок выбора книг не играет роли. Здесь важен только их состав. Как известно из предыдущего (см. задачу 5), число размещений из 10 по 4 равно А410=5040. Пусть теперь выбраны 4 книги из 10. Число таких возможных выборов, где не учитывается порядок выбранных книг, равно С410. Однако каждому из этих сочетаний будут соответствовать Р4=24 перестановки выбранных книг. Тогда выбор 4 книг из 10 с учетом их порядка по правилу умножения возможен С410 ∙ Р4 способами. С другой стороны, число указанных способов – это число размещений А410. Таким образом, число возможных способов выбора подарка равна 210.
Теорема.Число сочетаний из n элементов по m равно

Пример 11. Имеется 10 белых и 5 черных шаров. Сколькими способами можно выбрать 7 шаров, чтобы среди них были 3 черных?
Решение. Среди выбранных шаров 4 белых и 3 черных. Белые шары можно выбрать С410 =10!/4!∙6!=210 способами. Черные шары можно выбрать С35 =5!/3!∙2!=10 способами. Тогда по правилу умножения искомое число способов равно С410 ∙ С35 =2100.
Пример 12. Десять команд участвуют в розыгрыше первенства России по хоккею, лучшие из которых занимают 1-е, 2-е и 3-е места. Две команды, занявшие последние места, не будут участвовать в следующем таком же первенстве. Сколько разных вариантов результата первенства может быть, если учитывать только положение первых трех и последних двух команд?
Решение. Первые три места могут быть распределены А310=10!/7!=720 способами. В результате останется семь команд, две из которых выбывают из следующего первенства. Так как в этом случае порядок выбывших команд не важен, то это может произойти С27=7!/2!∙5!=21 способами. Согласно правилу умножения получаем, что число разных результатов первенства равно А310∙ С27=15 120. [4]
Упражнения для закрепления
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?
5. Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо?
6. Из трех математиков и десяти экономистов надо составить комиссию, состоящую из двух математиков и шести экономистов. Сколькими способами это можно сделать?
7. Вычислить:
1)  2)
2) 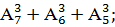 3)
3) 
8. Решите уравнения:
1)  ; 2)
; 2)  3)
3)  4)
4) 
Контрольные вопросы
1. Что является предметом изучения комбинаторики?
2. Сформулируйте правило произведения и правило сложения.
3. Какие соединения называют размещениями?перестановками
4. Какие множества называют упорядоченными?
5. Какие соединения называют сочетаниями?
6. Дайте определение факториала.
Дата добавления: 2018-02-28; просмотров: 782; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
