Лекция. Уравнение равновесия звезды
Для звезды, находящейся в равновесии, сила гравитационного притяжения, действующая на какой-либо элемент массы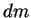 
, должна быть скомпенсирована равной по величине и противоположной по направлению силой. Такая уравновешивающая гравитацию сила в звездах обусловлена давлением вещества (точнее, градиентом давления).
В общем случае давление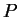 
является величиной, позволяющей описать силу, действующую на выделенный в жидкости или газе объем 
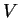произвольной формы со стороны окружающего его вещества, как интеграл по разделяющей поверхности
|
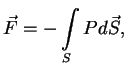
где давление 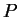зависит только от состояния вещества на этой поверхности. Вектор 
( 
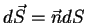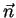-- нормаль к элементу поверхности 
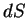) направлен в любой точке наружу от поверхности. Размерность давления 
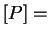дин/см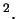 
Для жидкости, в которой давление однородно (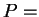 
const), имеем очевидное выражение для силы, действующей на замкнутую поверхность: 
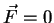. Пусть теперь давление неоднородно. В общем случае в малой окрестности некоторой точки, раскладывая в ряд, можно записать:
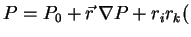 вторые производные 
|
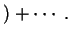
Подставляя найдем, что с точностью до величин второго порядка малости сила, действующая на объем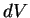 
, ограниченный поверхностью 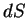, равна 
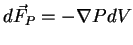, т.е. сила давления является объемной силой -- она пропорциональна 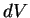и направлена из области большего давления в область меньшего. Масса объем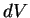а равна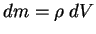 
. Сила гравитационного притяжения, которая является массовой силой, равна 
.
|
|
|
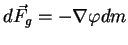В равновесии для невращающейся звезды эти две силы должны компенсировать друг друга, т.е.
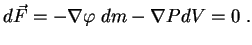
Окончательно условие механического равновесия записывается в виде
|
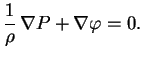
| Рис. 7. |
Для сферически-симметричных звезд уравнение гидростатического равновесия имеет вид
|
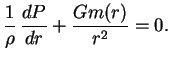
Сила гравитационного притяжения направлена к центру звезды. Уравновешивающая сила давления пропорциональна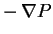 
, т.е. для поддержания равновесия звезды давление должно с необходимостью монотонно расти от поверхности к центру звезды.
Выделим внутри звезды единичный цилиндрический объе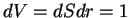м ( 
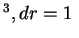см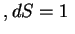 
см 
см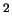 
) так, чтобы основания цилиндра были перпендикулярны радиусу. Для такого объема сила, обусловленная давлением, равна 
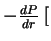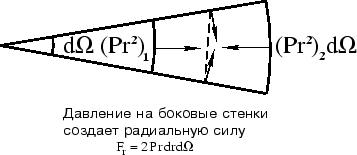
дин/см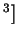 
. Выделим теперь шаровой сектор с раствором телесного угла 
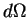. Казалось бы, поскольку сила давления на внешнюю поверхность шарового сектора равна 
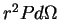, то результирующая сила давления, действующая на единичный объем этого сектора, равна 
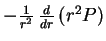. Не будет ли более правильным подставлять это выражение в вместо величины 
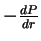? Оказывается нет. При выводе силы, действующей на шаровой сектор, мы не учли давление на боковые поверхности сектора, что дает добавочную силу вдоль радиуса 
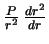. С учетом последнего мы опять приходим к выражению для силы газового давления .
|
|
|
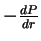В общем случае неизотропного давления следует применять выражение
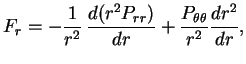
где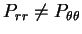 
. Для обычных газовых звезд давление изотропно - выполняется закон Паскаля: 
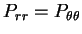и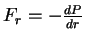 
.
Предположим, что нам известно уравнение состояния в виде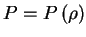 
, т.е. давление является функцией только плотности. Зададимся значениями в центре 
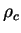и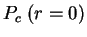 
. Тогда имеем систему двух обыкновенных дифференциальных уравнений первого порядка:
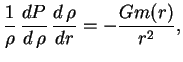
| (1.7) |
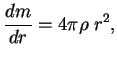
| (1.8) |
решая которую, получаем распределение плотности и давления вдоль радиуса.
Рассмотрим асимптотическое поведение решения в центре (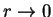 
) и на краю звезды ( 
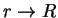). При 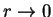получим
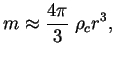
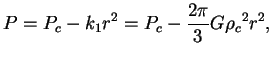
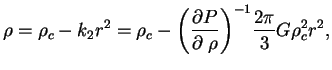
т.е. в центре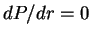 
и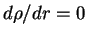 
.
На краю звезды имеем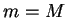 
и, интегрируя уравнение равновесия, получим
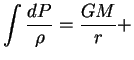const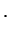 
Для того чтобы звезда имела определенную внешнюю границу, интеграл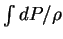 
должен сходиться при 
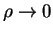. Например, для изотермической атмосферы 
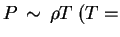const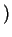 
интеграл расходится, т.е. изотермическая атмосфера должна быть бесконечна.
Если давление является степенной функцией плотности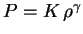 
, то необходимым (но не достаточным) условием конечности атмосферы является 
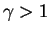. В этом случае
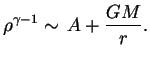
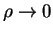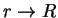Из условия при получим 
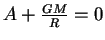и
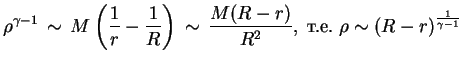
вблизи края звезды. Для частного, но встречающегося часто случая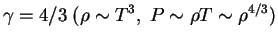 
, получим 
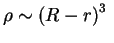при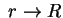 
.
|
|
|
|
| Рис. 8. |
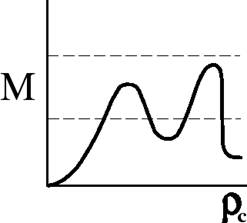
При определенном уравнении состояния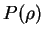 
не всегда можно решить задачу для данной массы (может оказаться, что решений для выбранной массы вообще не существует). Однако, задаваясь центральной плотностью 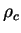, можно найти набор решений с различными массами, т.е. построить кривую 
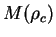. После этого уже видно, какие решения соответствуют данной массе, при каких массах существуют решения (т.е. состояния равновесия) и т.п.
Такой же подход применим и в ОТО. Качественно все остается по-прежнему: решение можно находить, интегрируя от центра, так как внешние слои не создают ускорения.
Дата добавления: 2018-02-28; просмотров: 818; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!