Для получения зачета без написания билета и решения задачи необходимо в тетради иметь решение следующих задач

На 3ку

Решить пример

Пример 22. Найти вероятность того, что при подбрасывании трех монет: a) только на одной из них появится «герб»;

Пример 22. Найти вероятность того, что при подбрасывании трех монет: b) хотя бы на одной монете появится «герб».

Пример 31. В урне 4 черных и 5 белых шаров. Из урны случайным образом вынимают 3 шара. Найти вероятность того, что среди вынутых шаров:

b) все шары одного цвета;

c) 2 белых шара;

Пример 44. Имеются две урны: в первой – 3 белых и 2 черных шара, во второй – 4 белых и 6 черных шаров. Из каждой урны вынимают наугад по одному шару. Найти вероятность того, что вынутые шары разного цвета.

Пример 51. Имеются две урны: в первой – 2 белых и 3 черных шара, во второй – 4 белых и 1 черный шар. Найти вероятность того, что извлеченный наудачу шар из наудачу выбранной урны окажется белым.

Пример 52. В группе студентов, пришедших на зачет, 30% подготовлены отлично, 50% – хорошо, 20% – посредственно. Всего имеется 30 билетов. Отлично подготовленный студент знает все билеты, хорошо подготовленный – знает только 25, посредственно – 15. Найти вероятность того, что вызванный наугад студент знает попавшийся ему билет.

Пример 54. Имеются три урны: в первой – 2 белых и 3 черных шара, во второй – 4 белых и 1 черный шар, в третьей – 3 белых и 2 черных шара. Извлеченный наудачу шар из наудачу выбранной урны оказался белым. Найти вероятность того, что: а) вынимали из первой урны; b) вынимали из второй урны; с) вынимали из третьей урны.

Пример 4. Монету подбрасывают 8 раз. Какова вероятность того, что 6 раз она упадет «гербом» вверх?

Пример 33. На отрезок АВ длины 4 см наудачу поставлена точка С. Найти вероятность того, что каждый из полученных отрезков АС и СВ имеет длину большую, чем 1 см.

Пример 55. Имеются три урны: в первой – 2 белых и 3 черных шара, во второй – 4 белых и 1 черный шар, в третьей – 3 белых и 2 черных шара. Извлеченный наудачу шар из наудачу выбранной урны оказался белым. Найти вероятность того, что: а) вынимали из первой урны; b) вынимали из второй урны; с) вынимали из третьей урны.

Пример 5. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 5000 рублей и 10 выигрышей по 1000 рублей. Найти закон распределения (ряд распределения), математическое ожидание и дисперсию случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета.

Задача 6. Случайная величина X задана функцией плотности вероятности

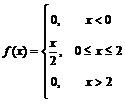
Найти функцию распределения F(x) случайной величины X. Построить графики плотности вероятности и функции распределения. Вычислить для X ее математическое ожидание, дисперсию, моду и медиану.

На 4ку

Решить задачу

31. Имеются две урны, в каждой из которых содержится 1 белый, 1 черный и 1 красный шар. Из обеих урн вынимают наугад по шару. Найти вероятность того, что: а) оба вынутых шара белые; b) оба вынутых шара одного цвета; с) среди вынутых шаров ровно один черный; d) среди вынутых шаров есть красные; е) среди вынутых шаров нет белых.

32. В учебном корпусе имеются 2 столовые. Три студента независимо друг от друга идут на обед, причем каждый из них выбирает для себя какую-то одну из этих двух столовых наугад. Найти вероятность того, что: а) все три студента придут в одну столовую; b) все три студента придут в первую столовую; с) в первую столовую придет только один студент.

47. В бригаде 4 женщины и 3 мужчины. Среди членов бригады разыгрываются 4 билета в театр. Какова вероятность того, что среди обладателей билетов женщин и мужчин окажется поровну?

52. В пакетике 4 красных и 6 зеленых леденцов. Найти вероятность того, что вынутые наудачу из пакетика 3 леденца окажутся одного цвета.

103. Вероятность попадания в цель первым стрелком 0.7, а вторым – 0.8. Стрелки выстрелили одновременно. Какова вероятность того, что один из них попадет в цель, а другой не попадет?

128. В группе спортсменов 20 пловцов, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для пловца – 0.9, для велосипедиста – 0.8 и для бегуна – 0.75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит квалификационную норму.

142. В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0.95, а при выстреле из винтовки без оптического прицела – 0.8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?

4. В результате каждого визита страхового агента договор заключается с вероятностью 1/4. Найти вероятность того, что из 10 визитов страхового агента 5 закончатся заключением договора?

Пример 34. Автобус ходит с интервалом 20 мин. Найти вероятность того, что человеку, пришедшему на остановку в произвольный момент времени, придется ждать не более 5 минут.

144. В пирамиде стоят 20 винтовок, из них 5 с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, может поразить мишень с вероятностью 0.8, а стреляя из винтовки без оптического прицела, – с вероятностью 0.5. Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.

Задача 2. Фирма участвует в 2 проектах, первый проект может закончиться удачей с вероятностью 0.7, второй – 0.6. В случае удачи какого-либо проекта фирма получает прибыль 800 т.р. за проект. Случайная величина X – размер прибыли фирмы при реализации этих проектов. Постройте ряд распределения, функцию распределения и найдите математическое ожидание, дисперсию, СКО и моду СВ X.

Задача 6. Случайная величина X задана функцией плотности вероятности

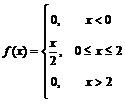
На 5ку

Решить задачу подобную лекционным

Пример 22. Найти вероятность того, что при подбрасывании трех монет: a) только на одной из них появится «герб»; b) хотя бы на одной монете появится «герб».

b) все шары одного цвета;

c) 2 белых шара;

Пример 4. Монету подбрасывают 8 раз. Какова вероятность того, что 6 раз она упадет «гербом» вверх?

Пример 53. Имеются две урны: в первой – 3 белых и 2 черных шара; во второй – 5 белых и 3 черных шара. Из первой урны во вторую перекладывают, не глядя, два шара. После этого из второй урны берут наугад один шар. Найти вероятность того, что этот шар будет белым.

Пример 45. Студент сдает три экзамена. Вероятность того, что он сдаст первый экзамен, равна 0.7, второй – 0.8, третий – 0.9. Найти вероятность того, что студентом будет сдан только один экзамен.

Задача 6. Случайная величина X задана функцией плотности вероятности

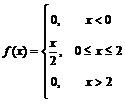
Для получения зачета без написания билета и решения задачи необходимо в тетради иметь решение следующих задач

Задача 6. Случайная величина X задана функцией плотности вероятности

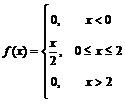
Дата добавления: 2018-02-28; просмотров: 531; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!