Построение линии среза тела вращения
ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ МОРСКОГО И РЕЧНОГО ФЛОТА
ИМЕНИ АДМИРАЛА С.О.МАКАРОВА»
________________________________________________________________
ИНСТИТУТ ВОДНОГО ТРАНСПОРТА
Кафедра основ инженерного проектирования
Т.О. Карклина
Начертательная геометрия и инженерная графика
ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ
Санкт-Петербург
2016
УДК 514.18
ББК 22.151.3
Рецензент:
Кандидат технических наук, доцент В.Я. Готлиб
Т.О.Карклина. Начертательная геометрия и инженерная графика. Проекционное черчение. Часть 1.:Методические указания. СПБ.: ГУМРФ им. адмирала С.О.Макарова, 2016.-51 с.
Изложены основные понятия и правила выполнения и чтения машиностроительных чертежей. Приведены положения единой системы конструкторской документации, определяющие эти правила.
Предназначены для студентов специальности
26.03.02 «Кораблестроение, океанотехника и системотехника объектов морской инфраструктуры» всех форм обучения.
13.03.02 « Электроэнергетика и электротехника»
08.03.02. «Строительство»
20.03.02. «Природообустройство и водопользование»
23.03.03. «Эксплуатация транспортно-технологических
машин и комплексов»
УДК 514.18
ББК 22.151.3
© Т.О.Карклина, 2016
© Государственный университет морского и речного флота
имени адмирала С.О.Макарова, 2016
Введение
Проекционное черчение является составной частью курса начертательной геометрии, используя ее основные положения, как теоретическую основу курса черчения, и предусматривает отработку навыков отображения пространственных тел на плоскости.
Работа по проекционному черчению в первой части включает в себя серию задач на построение простейших геометрических тел со сквозными отверстиями, а также задачи по построению линии среза на деталях, представляющих собой комбинацию тел вращения.
Общие указания по выполнению задания
Выполнение заданий осуществляется студентами в соответствии со своим вариантом (он определяется по порядковому номеру фамилии исполнителя в групповом журнале) на отдельных листах чертежной бумаги формата А4 (210х297) в соответствии с ГОСТ 2.301-68.
На каждом листе выполняется рамка, основная надпись и текстовые пояснения (при необходимости) шрифтом согласно ГОСТ 2.304-81. Изображения должны быть крупными и четкими. Тип линий выбирается в соответствии с ГОСТ 2.303-68.
Все листы с выполненными заданиями подписываются преподавателем и вместе с титульным листом (приложение 1) брошюруются в альбом.
Образцы выполненных чертежей приведены в приложениях 2 – 7.
Проецирование геометрических тел.
Любая машиностроительная деталь представляет собой сочетание различных простейших геометрических тел – цилиндра, призмы, конуса, сферы и пр.
При отображении пространственных тел на плоскости используется принцип ортогонального проецирования. Для определения проекций характерных точек, лежащих на поверхности тела, используют вспомогательные образующие или вспомогательные секущие плоскости.
Принцип использования вспомогательных образующих основан на свойстве принадлежности точки прямой линии. А если точка принадлежит любой линии, лежащей на поверхности тела, то она принадлежит этой поверхности. В качестве такой линии выбираем образующую n, проведенную по поверхности пирамиды (рис. 1), на которой лежит точка А.

Рис.1. Метод вспомогательных образующих на примере пирамиды.
Фронтальная проекция точки Алежит на фронтальной проекции образующей n’’. Для определения положения горизонтальной и профильной проекций точки А, сначала строим горизонтальную n’ и профильную n’’’проекции образующей n на поверхности пирамиды, а затем по правилам ортогонального проецирования находим положение фронтальной и профильной проекций точки А.
Аналогичным образом реализуется способ вспомогательных образующих и на поверхности конуса (рис. 2).
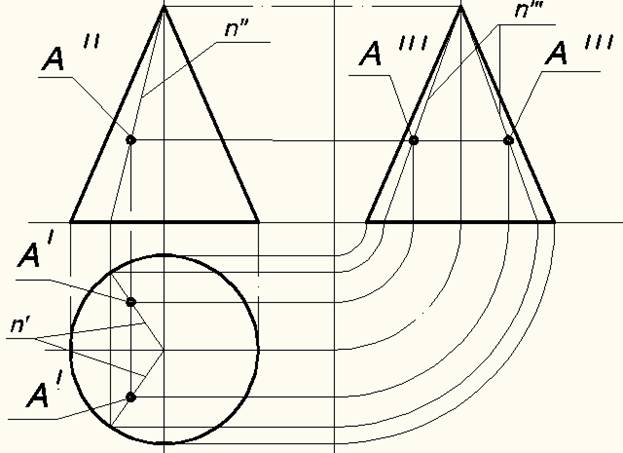
Рис. 2. Метод вспомогательных образующих на примере конуса.
Вспомогательные секущие плоскости используются для определения недостающих проекций точек на поверхности пирамиды, конуса и сферы.
Так, для определения горизонтальной и профильной проекций точки А при заданной ее фронтальной проекции (рис. 3, 4), через фронтальную проекцию точки проводится вспомогательная горизонтальная секущая плоскостьα. На горизонтальной проекции строится линия пересечения этой плоскости с поверхностью тела. Для пирамиды и конуса это фигура, подобная основанию, т.е. для конуса – окружность соответствующего радиуса (рис. 3), а для пирамиды – многоугольник (рис. 4). Искомая горизонтальная проекция точки будет находиться на линии пересечения вспомогательной плоскости с поверхностью тела. Для определения проекций N-го количества точек, лежащих на поверхности тела, используется N секущих плоскостей.

Рис. 3. Метод секущих вспомогательных плоскостей на примере конуса.

Рис. 4. Метод секущих вспомогательных плоскостей на примере пирамиды.
Изображение призмы.
Призма – это гранная фигура, у которой верхнее и нижнее основания являются многоугольниками. Элементы призмы: два основания, боковые грани, боковые ребра, ребра основания, вершины. На рис. 5 изображена прямоугольная призма со сквозным отверстием. Прямоугольной называется призма, у которой боковые поверхности перпендикулярны основаниям. Любая точка, лежащая на боковых поверхностях такой призмы, на виде сверху проецируется на контур основания (точки 1' – 10' на рис. 6).
В задании студентам дается два вида призмы – главный (фронтальный) и вид сверху (рис. 6). Построение вида слева призмы осуществляется в
такой последовательности:
- обозначают фронтальные и горизонтальные проекции вершин;
- по двум проекциям вершин находят их профильные проекции;
- строится вид слева, используя метод параллельного ортогонального проецирования (линии связи проводятся тонкими линиями и не стираются).
Затем приступают к построению выреза призмы. Для этого необходимо обозначить фронтальные проекции характерных точек выреза. Затем определяют положение сначала горизонтальных проекций этих точек, а затем профильных. После определения видимости, характерные точки соединяют соответственно сплошными (видимые) или пунктирными (невидимые) линиями (рис. 5).

Рис.5. Прямоугольная призма со сквозным отверстием.

Рис.6. Проекции прямоугольной призмы со сквозным отверстием.
Изображения цилиндра.
Цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя основаниями. Цилиндр, у которого в основании лежит круг, а образующие перпендикулярны к плоскости основания, называется цилиндром вращения (рис. 7).
Любая точка, лежащая на боковой поверхности цилиндра вращения, на виде сверху будет располагаться на окружности (точки 1' – 10' на рис. 8),
которая на виде сверху представляет собой горизонтальную проекцию боковых поверхностей цилиндра (они перпендикулярны основанию).
При пересечении цилиндра плоскостью, фигура сечения зависит от угла наклона секущей плоскости к образующим. Так, если секущая плоскость перпендикулярна образующим, форма сечения представляет собой окружность; если параллельна образующим – прямоугольник; а если наклонена к образующим под произвольным углом, отличным от 90 градусов – эллипс.

Рис. 7. Цилиндр вращения со сквозным отверстием.
Для построения вида слева необходимо отметить все характерные точки выреза, а на наклонных линиях и промежуточные (минимум пять точек,
включая крайние). Определить их горизонтальные и профильные проекции, соединить с учетом видимости соответствующим типом линий. Плавные кривые строятся с использованием лекал.

Рис. 8. Проекции цилиндра со сквозным отверстием.
Изображение пирамиды.
Пирамида – гранная фигура, у которой основание является многоугольником, а боковые грани – треугольники, имеющие общую вершину (рис. 9). Элементы пирамиды: вершина, основание, боковые грани, боковые ребра, ребра основания.

Рис. 9. Пирамида со сквозным отверстием.
Принцип построения вида сверху и слева пирамиды такой же, как и для призмы. Для определения положения точек, лежащих на поверхности
боковых граней, используют вспомогательные образующие (раздел 3, рис. 1) или вспомогательные секущие плоскости (раздел 3, рис. 4).
Пример построения вида сверху и вида слева пирамиды со сквозным отверстием приведен на рис. 10.
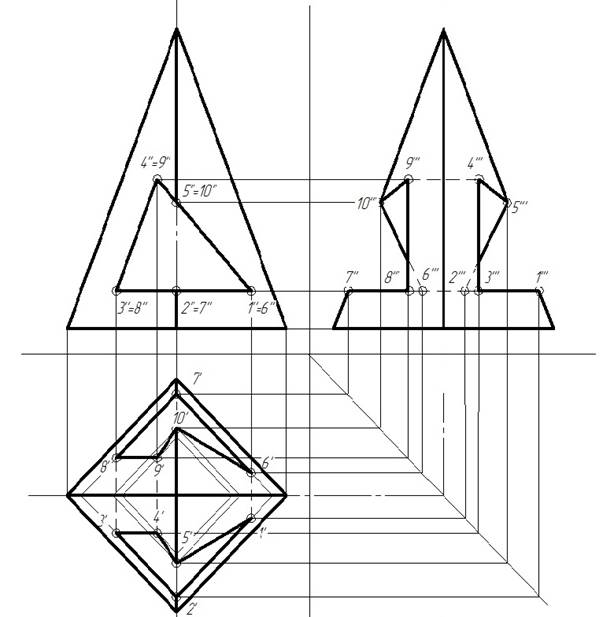
Рис. 10. Проекции пирамиды со сквозным отверстием.
Изображение конуса.
Конусом называется геометрическое тело, ограниченное конической поверхностью и плоским основанием. Конус, основанием которого является круг, а высота – перпендикуляр, опущенный из вершины на основание и проходящий через центр круга, называется конусом вращения (рис.11).

Рис. 11. Конус вращения.
На виде сверху конус проецируется в круг, центр которого является проекцией его вершины. На главном виде и виде слева - в равнобедренный
треугольник, основание которого равно диаметру окружности, а высота – высоте конуса (рис. 12).

Рис. 12. Проекции конуса вращения со сквозным отверстием.
Для определения проекций точек, лежащих на поверхности конуса вращения, может быть использован метод вспомогательных образующих (раздел 3, рис. 2) или вспомогательных секущих плоскостей (раздел 3,
рис. 3).
Линией пересечения боковой поверхности прямого кругового конуса с секущей плоскостью могут быть (рис. 13):
- две прямые-образующие конуса, если секущая плоскость проходит через вершину конуса (рис. 14);
- окружность, если секущая плоскость перпендикулярна оси конуса;
- парабола, если секущая плоскость параллельна одной из образующих конуса;
- гипербола, если секущая плоскость параллельна двум образующим конуса;
- эллипс, если секущая плоскость пересекает все образующие конуса и не перпендикулярна его оси.

Рис. 13. Форма линии пересечения секущих плоскостей с поверхностью прямого кругового конуса в зависимости от их расположения.
Для определения вида сверху и слева требуется построить горизонтальные и профильные проекции точек, принадлежащих вырезу; а также промежуточные точки, необходимые для проведения плавных лекальных линий.

Рис. 14. Секущая плоскость проходит через вершину конуса.
Изображение шара.
Шаром называется тело вращения, ограниченное сферической поверхностью, все точки которой одинаково удалены от центра «О» (рис.15). Любая ось, проходящая через центр шара, является осью симметрии. А любая плоскость, включающая центр шара, является плоскостью симметрии.
Шар проецируется на все три плоскости проекций в виде круга. Любая плоскость пересекает сферическую поверхность по окружности. Если угол зрения на секущую плоскость не равен 90 градусам, форма сечения сферической поверхности проецируется в эллипс.

Рис. 15. Шар со сквозным отверстием.
Для определения линии выреза на виде сверху и слева необходимо построить горизонтальные и профильные проекции точек, принадлежащих вырезу (точки 1,2,5,8,9) , а также промежуточные точки (точки 3,4,6,7) которые соединяют плавной кривой с использованием лекала.
Для построения проекций точек используется способ вспомогательных секущих плоскостей (рис. 16).
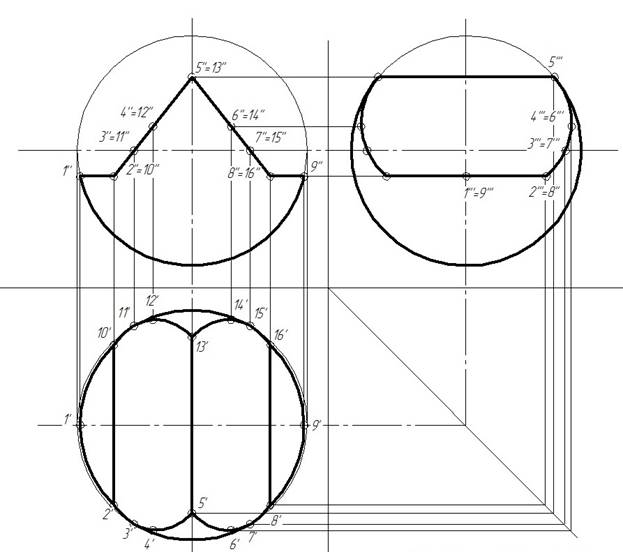
Рис. 16. Проекции шара со сквозным отверстием.
Построение линии среза тела вращения.
В практике часто встречаются задачи на построение линии среза на деталях, представляющих собой комбинацию тел вращения. В качестве примера на рис.17 изображено тело вращения, срезанное с обеих сторон плоскостями, параллельными фронтальной плоскости проекций.
Приведенная на рисунке деталь состоит из полушара, конуса и цилиндра.
Поверхности указаны в последовательности их расположения слева направо.

Рис. 17. Тело вращения с линией среза.
На видах сверху и слева линия среза проецируется в виде прямых, совпадающих со следами фронтальных плоскостей,которые расположены симметрично относительно оси детали (рис.18).
Для построения линии среза на фронтальной проекции используется метод секущих вспомогательных плоскостей. Каждая из проведенных
профильных плоскостей пересекает поверхность тела вращения по окружностям, которые проецируются на профильную плоскость без
искажения. Пересечение каждой такой окружности со следами плоскости среза определяет положение профильных проекций точек, принадлежащих искомой линии среза (например, точка 1'''). Фронтальную проекцию точки
находят проведя линию связи от точки 1''' до соответствующей вспомогательной профильной секущей плоскости, получив в данном примере точку 1''. Таким же образом строят фронтальные проекции остальных точек линии среза, и соединяют их сплошной линией видимого контура.
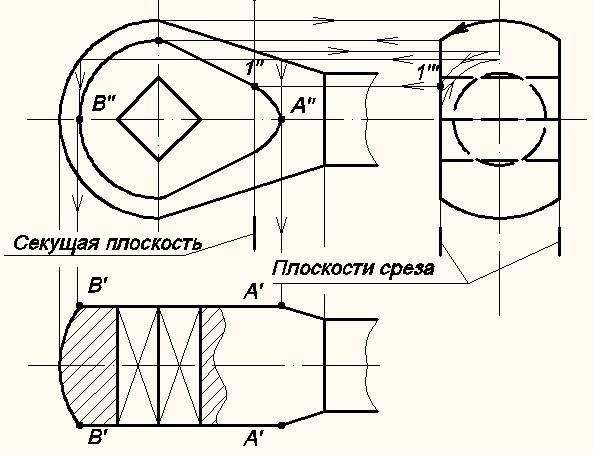
Рис. 18. Построение линии среза.
В процессе построения линии среза на фигуре, представляющей собой комбинацию тел вращения, необходимо помнить о закономерностях при сечении таких тел плоскостью. Так, например, при пересечении шара плоскостью получается окружность, цилиндра (плоскостью параллельной образующим) – прямоугольник и т.д.
Характерные точки «А''» и «B''» определяют следующим образом: сначала находят окружность, вписанную между следами фронтальных плоскостей среза на видеслева, а затем находится то место на фронтальной проекции детали, где ее диаметр равен диаметру вписанной окружности.
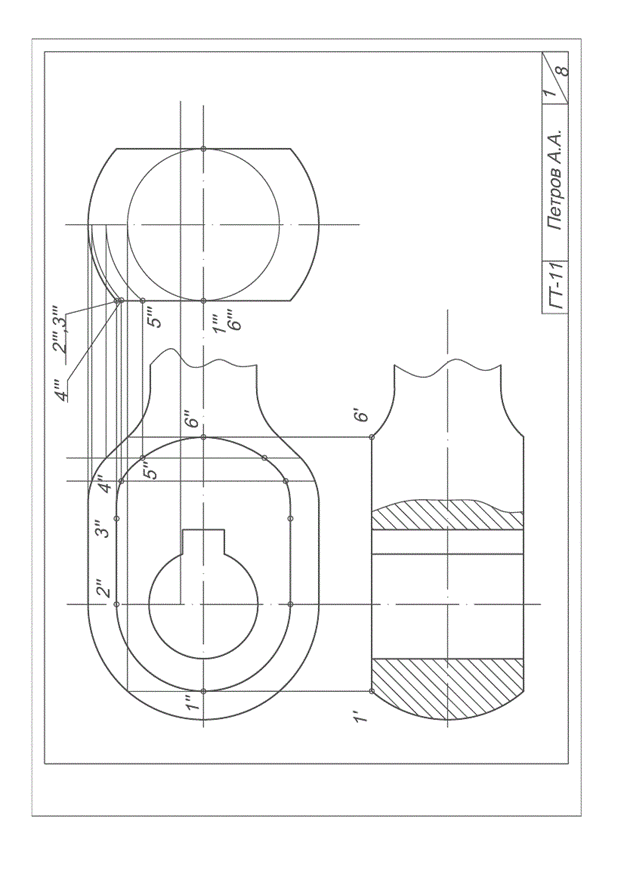
Работа по построению линии среза детали вращения выполняется на формате А3 (420х297).
Вначале студенты переносят на лист ватмана задание в соответствии с указанными размерами, в масштабе 1:1. Затем выполняют построение линии среза. После этого строиться вид сверху. Если в детали имеются отверстия,
на виде сверху выполняется разрез.
В приложении приведены примеры графического оформления титульного листа и основной надписи чертежей, а также примеры решения задач:
Приложение 1. Пример графического оформления титульного листа.
Приложение 2. Пример графического оформления и решение задачи на пересечение поверхности прямоугольной призмы сквозным отверстием.
Приложение 3. Пример графического оформления и решение задачи на пересечение поверхности цилиндра вращения сквозным отверстием.
Приложение 4. Пример графического оформления и решение задачи на пересечение поверхности конуса сквозным отверстием.
Приложение 5. Пример графического оформления и решения задачи на пересечение поверхности шара сквозным отверстием.
Приложение 6. Решение задачи на построение линии среза тела вращения.
Приложения
Приложение 1

Приложение 2

Приложение 3

Приложение 4

Приложение 5
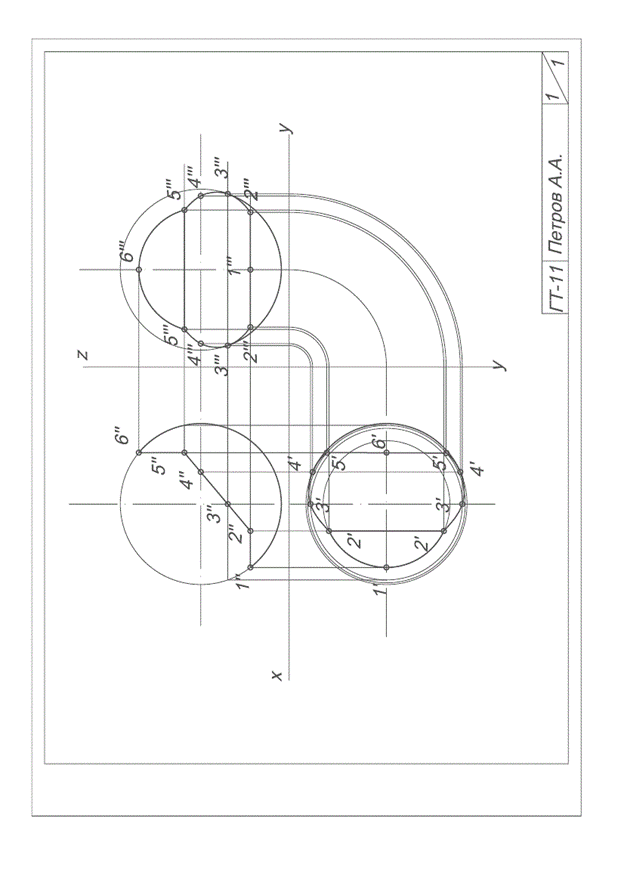
Приложение 6
Библиографический список
1. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. М.: Высшая школа, 2009. 272 с.
2. Манцветова И.В., Маянц Д.Ю., Гамиченко К.Я. Проекционное черчение с задачами. М.: Высшая школа, 1978. 344 с.
3. Единая система конструкторской документации. Сборник государственных стандартов. М.: Издательство стандартов, 2007.
Содержание
Введение……………………………………………………………….. 3
1. Общие указания по выполнению задания ………………………...4
2. Проецирование геометрических тел……………………………….5
3. Изображение призмы………………………………………………..8
4. Изображение цилиндра……………………………………………..10
5. Изображение пирамиды…………………………………………….13
6. Изображение конуса………………………………………………...15
7. Изображение шара…………………………………………………..18
8. Построение линии среза тела вращения…………………………...20
Приложения………………………………………………………….24-29
Библиографический список……………………………………………30
Карклина Татьяна Осиповна
Кандидат технических наук,
профессор кафедры основ инженерного проектирования
Дата добавления: 2018-02-28; просмотров: 9008; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
