Законы распределения погрешности измерений
При использовании вероятностного подхода к описанию погрешности требуется знание законов распределения погрешности измерений. Встречающиеся в метрологии законы распределения можно свести к следующим:
- трапецеидальные (плосковершинные);
- экспоненциальные;
- уплощенные (приблизительно плосковершинные);
- семейство распределений Стьюдента;
- двухмодальные.
К трапецеидальным относятся равномерное, собственно трапецеидальное, составленное как композиция из двух равномерных законов, имеющих различную ширину и треугольное распределение, представляющее собой частный случай предыдущего (при равной ширине составляющих равномерных распределений). Равномерное распределение (рис. 1) имеют погрешности квантования в цифровых приборах, округления при отсчете показаний стрелочного прибора, от трения в стрелочных приборах и т.д. 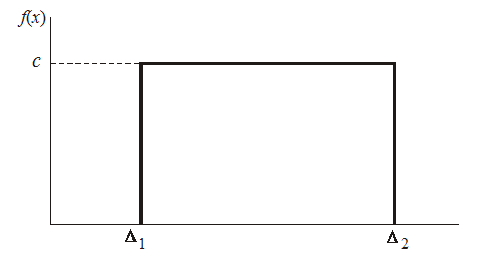
Рис. 1. Равномерный закон распределения случайной погрешности Δ
При равномерном законе распределения случайная погрешность Δ принимает значения лишь в пределах конечного интервала Δ1 - Δ2 с постоянной плотностью вероятностей р(x). Математически равномерный закон выглядит так:
p(Δ)=с, при Δ1≤Δ≤Δ2 ;
p(Δ)=0, при Δ1>Δ>Δ2 ,
Площадь под кривой распределения равна единице: с(Δ2 - Δ1) = 1, отсюда
c=1/(Δ2-Δ1) .
Тогда формула примет вид
p(Δ)=1/(Δ2-Δ1) , при Δ1≤Δ≤Δ2 ;
p(Δ)=0, при Δ1>Δ>Δ2 .
Математическое ожидание и среднее квадратическое отклонение случайной погрешности Δ
M(Δ)=(Δ2+Δ1)/2 ;
σ=(Δ2-Δ1)/2√3 .
Как уже указывалось, моды у равномерного закона распределения не имеется.
Математическая зависимость нормального закона
Одним из экспоненциальных законов распределения является так называемое нормальное распределение (распределение Гаусса). Закон распределения погрешностей результата измерения принято считать нормальным в том случае, когда полная погрешность образуется из большого числа независимых случайных составляющих (частных погрешностей), независимо от их законов распределения, при условии, что ни одна из этих частных погрешностей не преобладает над всеми остальными.
Формула для плотности вероятности нормального распределения погрешностей имеет следующий вид:
p(Δ)=1/(σ√(2π))∙exp[-(Δ-M(Δ))/(2σ2)] .
Как видно из формулы, нормальный закон полностью характеризуется двумя числовыми характеристиками - математическим ожиданием M(Δ) и дисперсией σ. Колоколообразная кривая нормального распределения симметрична относительно оси ординат. Это означает, что погрешности, одинаковые по величине, но противоположные по знаку, встречаются одинаково часто. Кроме того, малые погрешности встречаются чаще, чем большие. Данные свойства иллюстрирует рис. 2. Так, площадь под кривой плотности распределения вероятности в интервале Δ2-Δ1 существенно больше, чем площадь в равном интервале Δ4-Δ3. Площадь же под кривой плотности распределения вероятностей характеризует вероятность появления погрешностей.

Рис. 2. График p(Δ) для нормального закона распределения случайной погрешности
Рис. 3 иллюстрирует изменение формы кривой плотности распределения вероятностей при различных значениях средних квадратических отклонений (σ1>σ2>σ3). Видно, что чем большее значение имеет σ, тем больше результаты измерений рассеянны, тем больше вероятность проявления больших погрешностей. Таким образом, чем меньше значение σ, тем выше качество измерений.

Рис. 3. Графики нормального закона распределения при различных значениях σ
Отметим, что рассмотренные выше законы распределения описывают поведение случайных непрерывных величин. На практике результаты измерений и соответствующие им случайные погрешности являются дискретными величинами. При использовании дискретных величин производится оценка параметров их законов распределений на основе выборок - определенного ряда значения измеряемой величины на основе n независимых наблюдений. К выборке предъявляется требование репрезентативности (представительства), т.е. она должна достаточно хорошо представлять пропорции генеральной совокупности случайных величин. На основе выборки определяются оценки параметров, которые сами являются случайными величинами, значения которых зависят от объема экспериментальных данных.
Таким образом, мерой степени согласия между результатами последовательно проводимых измерений одной и той же величины является повторяемость измерений, причем предполагается, что измерения производятся одним и тем же методом, на одной и той же аппаратуре, при неизменных рабочих условиях и в течение короткого отрезка времени. Чем выше повторяемость, тем меньше неопределенность результата многократного измерения. Воспроизводимость результата измерения характеризуется близостью результатов, получаемых при повторных измерениях одной и той же величины, выполняемых при различных условиях и режимах работы, растянутых на длительное время. Очевидно, что вследствие влияния систематических погрешностей воспроизводимость результата измерения обычно ниже, чем повторяемость.
Список литературы по лекциям 1-2
1. Раннев Г.Г.* Информационно-измерительная техника и электроника. М.: Академия, 2006, 512 с.
2. Авдеев Б.Я., Антонюк Е.М., Душин Е.М. Основы метрологии и электрические измерения. Академия. 2007.-376 с.
3. Новицкий П.В., Зограф И.А. * Оценка погрешностей результатов измерений.- Л.: Энергоатомиздат. С-Пб. Отделение, 2015.-248 с.
- Шахнин В.А.* Обработка результатов измерений. Методические указания по дисц. ИИТ и Э. Владимир: Изд-во ВлГУ. 2002. 51 с.
*Книги из фонда библиотеки ВлГУ
ЛЕКЦИЯ 3.
СРЕДСТВА ИЗМЕРЕНИЙ
План лекции:
3.1. Классификация средств измерений
3.2. Меры электрических величин
Дата добавления: 2018-02-28; просмотров: 7924; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
