Вычисление объемов земляных работ
Линия нулевых работ разбивает некоторые квадраты на геометрические фигуры (трапеция, прямоугольный треугольник, многоугольник). Все геометрические фигуры, образованные линией нулевых работ, нумеруются произвольно (рис.4). Число строк в ведомости объемов земляных работ равно числу фигур (таб.2).
Объем земляных работ вычисляется по формуле V = Sф·hср.,
где Sф – площадь геометрической фигуры,
hср. – средняя рабочая отметка фигуры.

Рис.3. Пример картограммы земляных работ.

М 1:500 h = 0,25м
Рис.4. Пример плана строительной площадки.
Для вычисления площадей фигур (квадрата, трапеции, прямоугольного треугольника) используются общие формулы геометрии. При вычислении площади в качестве сторон фигуры принимаются сторона квадрата a и расстояния d1 и d2, предварительно выписанные на картограмме. Площадь смежных фигур (например, фигуры 3 и 8) можно вычислять как дополнение до площади квадрата.
Пример: S1 = a2 = 202 = 400м2; S2 =  м2 ;
м2 ;
S3 = 400 – 264 = 136м2; S7 = 15,6·6,9/2 = 53,8м2; S8 = 400-53,8 = 346,2м2;
Средняя рабочая отметка фигуры вычисляется как среднее арифметическое (по модулю) из рабочих отметок вершин фигуры, учитывая и точку нулевых работ.
Например: h2ф ср. =  h7ф ср.=
h7ф ср.= 
Ведомость объемов земляных работ.
Таблица 2
| №№ фигур |
Sф, м2 |
hср., м | Объемы V,м3 | |
| Vнасыпь | Vвыемка | |||
| 1 | 400 | 0,47 | 188 | |
| 2 | 264 | 0,13 | 34,3 | |
| 3 | 136 | 0,08 | 10,9 | |
| 4 | … | … | … | |
| 5 | … | … | … | |
| 6 | … | … | … | |
| 7 | 53,8 | 0,08 | 43,0 | |
| 8 | 346,2 | 0,22 | 76,2 | |
∑ = 253,4 ∑ = 252,6
Вычисленные объемы земляных работ записывают в соответствующую графу ведомости (насыпь – выемка). Вычисляют суммарный объем насыпи и выемки. Вычисляют погрешность определения объемов земляных работ:

Примечание: суммарные объемы насыпи и выемки берутся по модулю.
Пример: δV=[(253.4-252.6)/(253,4+252,6)]·100 = 0,03%
КОНТРОЛЬНАЯ РАБОТА № 3
Работа состоит из двух заданий. Ответы на вопросы и выполнение всех заданий высылаются на рецензирование одновременно.
ЗАДАНИЕ 1. Ответы на вопросы по темам 11,12 раздела 2.
Геодезическое обеспечение изысканий, проектирования и строительства сооружений.
Студент должен ответить на 2 вопроса из списка вопросов для самостоятельной работы по темам 11,12. Номер вопроса, как и в контрольных работах №1,2, определяется последней цифрой шифра зачетной книжки. Требования к ответам на вопросы изложены в общих методических указаниях. В тех случаях, когда для пояснения ответа необходимы рисунок или чертеж, то они должны быть представлены.
ЗАДАНИЕ 2. Перенесение на местность проектов застройки и планировки.
Расчет разбивочных элементов для перенесения проекта на местность.
Литература: [5, гл. 3 §20]
Проектируемое сооружение привязано к опорной геодезической сети полярным способом.
Задание:выполнить расчет разбивочных элементов для перенесения на местность точек пересечения основных осей здания (А и В) – горизонтальных углов β и полярных расстояний d (рис.5).
Исходные данные:координаты опорных пунктов геодезической сети М и N - ХМ, УМ и ХN, УN; координаты точек пересечения основных осей здания – ХА, УА и ХВ, УВ.
Координаты точек А,В, N - общие для всех студентов.
Координаты точки М - ХМ, УМ – каждый студент изменяет с учетом своего номера варианта: ХМ = ХМ + 1м·Nв УМ = УМ + 1м·Nв,
где Nв – номер варианта, равный последней цифре шифра зачетной книжки студента.
Пример: Nв = 4
ХМ = 806,8м+1м·4 = 810,8м УМ =410,5м+1м·4 = 414,5м
Вариант задания.
| Х,м | У,м | |
| M | 806,80 | 410,50 |
| N | 795,70 | 491,80 |
| A | 825,30 | 416,20 |
| B | 832,40 | 470,50 |
Разбивочные углы β1 и β2 вычисляют как разность дирекционных углов α двух смежных направлений (рис.5). Дирекционные углы линий, образующих разбивочные углы β, вычисляют по координатам конечных точек проекта (А,В) и опорных пунктов (М,N) решением обратной геодезической задачи по формулам:
tg r =  ; tg rМА =
; tg rМА =  ; tg rNB =
; tg rNB =  ;
;

Рис.5.
По алгебраическим знакам числителя и знаменателя определяют румбы линий r и дирекционные углы α (таб.3).
Таблица 3.
| Знаки приращений |
Четверть | Формула связи α и r | |
| ± ∆х | ± ∆у | ||
| + | + | СВ | α = r |
| - | + | ЮВ | α = 180º- r |
| - | - | ЮЗ | α = 180º + r |
| + | - | СЗ | α = 360º - r |
По дирекционным углам линий вычисляют разбивочные углы β:
β1=αMN - αMA β2=αNB – αNM
Дирекционный угол αNM вычисляют как обратный направлению MN:
αNM = αMN ± 180º
Полярные расстояния d находят по формулам:
d = √ ∆х2 + ∆у2, d = ∆у/sin r, d = ∆х/cos r
Пример: tg rМА= 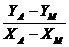 =
= 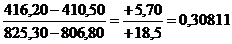
аrctg 0,30811 = 17,12459º = 17º07'
Приращения координат ∆x и ∆y имеют знаки «+» и «+» соответственно.
Следовательно румб rМА принадлежит I четверти.
rМА = 17º07' CB
В I четверти связь между румбом и дирекционным углом следующая:
α = r.
Следовательно αМА = 17º07'.
Полярное расстояние между точками А и М равно:
d1 = dМА = 5,70/0,29437 = 18,50/0,95571 = √5,72 + 18,52 = 19,36м
Вычисления остальных разбивочных элементов аналогичны.
Примечание: горизонтальные углы β1 и β2 должны быть положительными. В противном случае следует искать ошибку в вычислении дирекционных углов α.
СПИСОК ЛИТЕРАТУРЫ
ОСНОВНАЯ
1. Инженерная геодезия под ред. Д.Ш. Михелева, М., Высшая школа, 2001.
2. Практикум по инженерной геодезии под ред. В.Е.Новака, М., Недра, 1987.
ДОПОЛНИТЕЛЬНАЯ
3. Инженерная геодезия. Г.В. Багратуни, В.Н. Ганьшин, М., Недра, 1984.
4. Справочник по геодезическим работам в строительно-монтажном производстве под ред. Ю.В. Полищука, М., Недра, 1990.
5. Геодезическое обеспечение проектирования, строительства и эксплуатации зданий, сооружений. Т.И. Хаметов, М., АСВ, 2002.
6. Справочник по геодезии для строителей. М.П. Сироткин, М., 1987.
7. Прикладная геодезия. Н.П. Булгаков и др., М., Недра, 1990.
8. Строительные нормы и правила. СНиП 3.01.03-84. Геодезические работы в строительстве.
9. Условные знаки для топографических планов масштабов 1:5000, 1:2000, 1:1000 и 1:500, М., Картоцентр-Геодезиздат, 2000.
Дата добавления: 2018-02-28; просмотров: 10665; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
