Поверхности относимости. Референц-эллипсоид
Поверхность, которая соответствует принятой модели, называется поверхностью относимости. Т.е. реальная физическая поверхность Земли первоначально отображается на поверхность относимости.
В некоторых странах или группе стран во время обработки геодезических измерений используют эллипсоиды с параметрами, полученными по результатам геодезических работ на территории данной страны или нескольких стран. Такие «рабочие» эллипсоиды называются местными эллипсоидами или референц-эллипсоидами. Референц-эллипсоид можно рассматривать как эллипсоид, который наилучшим образом подходит только для некоторой части поверхности Земли.
В Украине, как и в России, а также в бывшем СССР, в качестве отсчетного эллипсоида используется референц-эллипсоид Красовского, который характеризуется следующими параметрами:
 Данный эллипсоид был принят в качестве рабочего в бывшем СССР в 1946 году.
Данный эллипсоид был принят в качестве рабочего в бывшем СССР в 1946 году.
Поскольку полярное сжатие референц-эллипсоида очень маленькое, то при решении многих задач за фигуру Земли принимают сферу, которая равна по объему земному эллипсоиду. Для референц-эллипсоида Красовского радиус такой сферы составляет 6371,11 км.
Параметры размеров Земли.
Размер Земли, так же, как и размер всех остальных небесных тел, измеряют по таким параметрам, как масса, плотность, объем, площадь поверхности и экваториальный/полярный/средний диаметр. Хотя мы живем на этой планете, очень немногие могут назвать значения для этих параметров. Ниже приведена таблица со значениями данных, которые используются для определения размера Земли.
|
|
|
Масса – 5 9736×1024 кг, Объем – 1.083×1012 км3, Средний диаметр – 12 742 км, Площадь поверхности – 510 072 000 км2, Плотность – 5.515 г/см3, Длина окружности – 40 041 км
ИЗОБРАЖЕНИЕ ЗЕМНОЙ ПОВЕРХНОСТИ НА ПЛОСКОСТИ
Метод проекций в геодезии
Изобразить земную поверхность на плоскости - значит изобразить на ней очертания различных предметов местности. Всякий контур - это непрерывный ряд точек. Изображение земной поверхности на плоскости сводится таким образом к изображению отдельных точек. При изображении на плоскости (листе бумаги) различных контуров земной поверхности все их точки проектируют со сложной физической поверхности Земли на более простую поверхность по перпендикулярам к этой поверхности (рисунок 1.10). Таковыми поверхностями могут быть поверхность земного эллипсоида, шара или плоскость.
11. Горизонтальная проекция
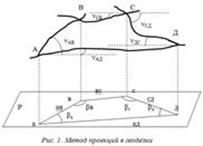 Для изображения физической поверхности Земли на бумаге ее сначала проецируют отвесными линиями на горизонтальную (уровенную поверхность). Поскольку отвесные линии перпендикулярны геоиду, то мы имеем ортогональную (прямоугольную) проекцию. В геодезии эта проекция называется горизонтальной. А, В, С, Д – точки физической поверхности, а, в, с, д – их горизонтальные проекции. Если наш участок имеет размеры, меньшие 25 км2, и его можно принять за горизонтальную плоскость.
Для изображения физической поверхности Земли на бумаге ее сначала проецируют отвесными линиями на горизонтальную (уровенную поверхность). Поскольку отвесные линии перпендикулярны геоиду, то мы имеем ортогональную (прямоугольную) проекцию. В геодезии эта проекция называется горизонтальной. А, В, С, Д – точки физической поверхности, а, в, с, д – их горизонтальные проекции. Если наш участок имеет размеры, меньшие 25 км2, и его можно принять за горизонтальную плоскость.
|
|
|
АВСД – четырехугольник в пространстве, авсд – его горизонтальная проекция. Участок менее 25 км2, Р – горизонтальная плоскость.
Проекция линии местности на горизонтальную плоскость называется горизонтальным проложением этой линии: ав есть горизонтальное проложение линии АВ и т.д.
Проекции пространственных углов на горизонтальную плоскость называются горизонтальными углами: вад, авс и т.д. есть горизонтальные углы.
Угол между линией местности и ее проекцией на горизонтальную плоскость называется углом наклона ее или вертикальным углом: ν1,ν2 и т.д. являются углами наклона.
Чтобы на листе бумаги изобразить горизонтальную проекцию участка местности, необходимо знать горизонтальные проложения линий и горизонтальные углы между ними. Горизонтальные проложения можно найти, если известно наклонное расстояние между точками и угол наклона: ав=АВ·соs ν1; вс =ВС· соs ν2
Таким образом, для получения проекций точек на горизонтальную плоскость необходимо знать три величины: наклонное расстояние, угол наклона (вертикальный угол) и горизонтальный угол. Именно эти три величины и измеряют в геодезии.
|
|
|
12. Центральная проекция
 Чтобы изобразить объемный предмет на плоском чертеже, применяют метод проекций. К простейшим проекциям относятся центральная и ортогональная проекции.
Чтобы изобразить объемный предмет на плоском чертеже, применяют метод проекций. К простейшим проекциям относятся центральная и ортогональная проекции.
При центральной проекции (рис.) проектирование выполняют линиями, исходящими из одной точки, которая называется центром проекции. Пусть требуется получить центральную проекцию четырехугольника ABCD на плоскость проекции P; центр проекции – точка S.
Проведем линии проектирования до пересечения с плоскостью проекции, получим точки a, b, c, d, являющиеся проекциями точек A, B, C, D. Плоскость проекции и объект могут располагаться по разные стороны от центра проекции; так при фотографировании центром проекции является оптический центр объектива, а плоскостью проекции – фотопластинка или фотопленка.
Дата добавления: 2018-02-28; просмотров: 2343; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
