Вычисление площадей плоских фигур
Применение определенного интеграла
Прямоугольные координаты. Пусть в прямоугольных координатах дана плоская кривая AB, уравнение которой y = f (x), где a ≤ x ≤ b (рис. 2).
Под длиной дуги AB понимается предел, к которому стремиться длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремиться к нулю. Применим схему I (метод сумм).
1.Точками X  = a, X
= a, X  , … , X
, … , X  =b (X
=b (X  ≤ X
≤ X  ≤ … ≤ X
≤ … ≤ X  ) разобьем отрезок [a, b] наn частей. Пусть этим точкам соответствуют точки M
) разобьем отрезок [a, b] наn частей. Пусть этим точкам соответствуют точки M  = A, M
= A, M  ,…, M
,…, M  = B на кривой AB.
= B на кривой AB.
Проведем хорды M  M
M  , M
, M  M
M  ,…, M
,…, M  M
M  , длины которых обозначим соответственно через ΔL
, длины которых обозначим соответственно через ΔL  ,ΔL
,ΔL  ,…, ΔL
,…, ΔL  .
.

Рис. 2
Получим ломанную M  M
M  M
M  … M
… M  M
M  , длина, которой равна L
, длина, которой равна L  = ΔL
= ΔL  + ΔL
+ ΔL  + … + ΔL
+ … + ΔL  =
=  ΔL
ΔL  .
.
2.Длину хорды (или звена ломанной) ΔL  можно найти по теореме Пифагора из треугольника с катетами ΔX
можно найти по теореме Пифагора из треугольника с катетами ΔX  и ΔY
и ΔY  :
:
ΔL  =
=  , где ΔX
, где ΔX  = X
= X  - X
- X 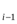 , ΔY
, ΔY  = f(X
= f(X  ) – f(X
) – f(X 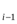 ).
).
По теореме Лагранжа о конечном приращении функции ΔY  =
=  (C
(C  ) ΔX
) ΔX  , где C
, где C 
 (X
(X 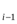 , X
, X  ). Поэтому ΔL
). Поэтому ΔL  =
=  =
=  ,
,
а длина всей ломанной M  M
M  M
M  … M
… M  M
M  равна
равна
L 
 =
=  ΔL
ΔL  =
= 
 . Длина кривой AB, по определению, равна L =
. Длина кривой AB, по определению, равна L =  L
L  =
= 
 ΔL
ΔL  . Заметим, что при ΔL
. Заметим, что при ΔL 
 0 также и ΔX
0 также и ΔX 
 0 (ΔL
0 (ΔL  =
=  и следовательно | ΔX
и следовательно | ΔX  | < ΔL
| < ΔL  ). Функция
). Функция  непрерывна на отрезке [a, b], так как, по условию, непрерывна функция f
непрерывна на отрезке [a, b], так как, по условию, непрерывна функция f  (X). Следовательно, существует предел интегральной суммы L
(X). Следовательно, существует предел интегральной суммы L  =
=  ΔL
ΔL  =
= 
 , кода max ΔX
, кода max ΔX 
 0:
0:
L = 

 =
= 
 dx.
dx.
Таким образом, L = 
 dx.
dx.
|
|
|
Пример 1. Найти длину окружности радиуса R. (рис. 3).
Решение:Найдем ¼ часть ее длины от точки (0;R) до точки (R;0). Так как y = 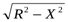 ,
,
¼L = 
 dx = R arcsin
dx = R arcsin 
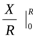 = R
= R  .
.
Значит L = 2  R.
R.
Полярные координаты
Пусть кривая AB задана уравнением в полярных координатах r = r(  ),
),  . Предположим, что r(
. Предположим, что r(  ) и r
) и r  (
(  ) непрерывны на отрезке [
) непрерывны на отрезке [  ]. Если в равенствах x = rcos
]. Если в равенствах x = rcos  , y = rsin
, y = rsin  , связывающих полярные и декартовы координаты, параметром считать угол
, связывающих полярные и декартовы координаты, параметром считать угол  , то кривую AB можно задать параметрически
, то кривую AB можно задать параметрически  , тогда
, тогда 
Поэтому  =
=  =
=

Применяя формулу L = 
 , получаем L =
, получаем L = 
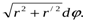
П  ример 2.Найти длину кардиоиды r = a(1 + cos
ример 2.Найти длину кардиоиды r = a(1 + cos  ).
).
Решение:Кардиоида r = a(1 +cos  ) симметрична относительно полярной оси. Найдем половину (рис. 4) длины кардиоиды:
) симметрична относительно полярной оси. Найдем половину (рис. 4) длины кардиоиды:
½ L = 
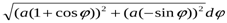 =
=
a 
 = a
= a 
 =
=
2a  cos
cos  d
d  = 4a sin
= 4a sin 
 = 4a.
= 4a.
Вычисление объема тела.
Произвольное ограниченное множество точек пространства будем называтьтелом.
Вычисление объема тела по известным площадям параллельных сечений.Пусть требуется найти объем V тела (рис. 5), причем известны площади сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ox: S = S(x), a≤ x≤ b.

Применим схему II (метод дифференциала).
1.Через произвольную точку x  [а; b]проведем плоскость П, перпендикулярную оси Ох. Обозначим через S(x) площадь сечения тела этой плоскостью; S(x) считаем известной и непрерывно изменяющейся при изменении x. Через v(x) обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на отрезке [а; x]величина v есть функция от x, т. е.v = у(x) (v(a) = 0, v(b) = V).
[а; b]проведем плоскость П, перпендикулярную оси Ох. Обозначим через S(x) площадь сечения тела этой плоскостью; S(x) считаем известной и непрерывно изменяющейся при изменении x. Через v(x) обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на отрезке [а; x]величина v есть функция от x, т. е.v = у(x) (v(a) = 0, v(b) = V).
|
|
|
2. Находим дифференциал dV функции v = v(x). Он представляет собой
“элементарный слой” тела, заключенный между параллельными плоскостями, пересекающими ось Ох в точках x и x + Δx, который приближенно может быть принят за цилиндр с основанием S(x) и высотой dx.Поэтому дифференциал объема dV = S(х) dх.
3.Находим искомую величину V путем интегрирования dА в пределах от a доb:
V =  S(x) dx
S(x) dx
Формула объема тела по площади параллельных сечений

Пример 3.Найти объем эллипсоида  (рис. 6).
(рис. 6).
Р
Рис. 6
ешение: Рассекая эллипсоид плоскостью,
параллельной плоскости OYZ и на расстоянии х от нее (-a≤ x≤ b.), получим эллипс

Площадь этого эллипса равна S(x) =  bc(1 -
bc(1 -  ). Поэтому, по формуле имеемV =
). Поэтому, по формуле имеемV =  bc
bc  (1 -
(1 -  )dx =
)dx = 
 abc.
abc.
Объем тела вращения
Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией у = f(х) ≥ 0, отрезком а ≤ х ≤ b и прямыми х = а и
х = b (рис. 7). Полученная от вращения фигура называется телом вращения.Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Oх), есть круг с радиусом у = f(х).Следовательно,  S(x)=
S(x)=  y
y  . Применяя формулу V =
. Применяя формулу V =  S(x) dx объема тела по площадипараллельных сечений, получаемV
S(x) dx объема тела по площадипараллельных сечений, получаемV  =
= 
 y
y  dx. Если криволинейная трапеция ограничена графиком непрерывной функции x =
dx. Если криволинейная трапеция ограничена графиком непрерывной функции x =  (x) ≥ 0 и прямыми x = 0, y = c, y = d (c < d), то объем тела, образованного вращением этой трапеции вокруг оси Оу, по аналогии с формулой
(x) ≥ 0 и прямыми x = 0, y = c, y = d (c < d), то объем тела, образованного вращением этой трапеции вокруг оси Оу, по аналогии с формулой
|
|
|
V =  S(x) dx, равен V =
S(x) dx, равен V = 
 x
x  dy.
dy.
Пример 4.Найти объем тела, образованного вращением фигуры, ограниченной линиями у = 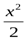 , x = 0, у = 2
, x = 0, у = 2  вокруг оси Оу.
вокруг оси Оу.
Решение: По формуле V = 
 x
x  dyнаходим:
dyнаходим:
V  =
= 
 2ydy =
2ydy =  y
y 
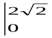 = 8
= 8  .
.
Пример 5.Найти объем тела, которое будет получено при вращении около оси абсцисс криволинейной трапеции у=1-х2, у=0.
Решение:Объем тела вычисляется по формуле V=  (x)dx. Найдем промежуток интегрирования 1-х2=0, имеем х1=1 и х2=-1. Поэтому V=
(x)dx. Найдем промежуток интегрирования 1-х2=0, имеем х1=1 и х2=-1. Поэтому V= 
 +
+ 
 +
+ 
 =
=  куб.ед.
куб.ед.
Пусть кривая АВ является графиком функции у = f(х) ≥ 0, где х  [а;b], а функция у = f(х) и ее производная у' = f'(х) непрерывны на этом отрезке.
[а;b], а функция у = f(х) и ее производная у' = f'(х) непрерывны на этом отрезке.
Найдем площадь S поверхности, образованной вращением кривой АВ вокруг оси Ох (рис. 8). Применим схему II (метод дифференциала).
1  . Через произвольную точку х
. Через произвольную точку х  [а; b] проведем плоскость П, перпендикулярную осиОх. Плоскость П пересекает поверхность вращения по окружности с радиусом у - f(х). Величина S поверхности части фигуры вращения, лежащей левее плоскости, является функцией от х, т. е. s = s(х)
[а; b] проведем плоскость П, перпендикулярную осиОх. Плоскость П пересекает поверхность вращения по окружности с радиусом у - f(х). Величина S поверхности части фигуры вращения, лежащей левее плоскости, является функцией от х, т. е. s = s(х)
|
|
|
(s(а) = 0 и s(b) = S).
2. Дадим аргументу х приращение Δх = dх.Через точку х + dх  [а; b]также проведем плоскость, перпендикулярную оси Ох. Функцияs = s(х) получит приращение Δs, изображенного на рисунке в виде “пояска”.
[а; b]также проведем плоскость, перпендикулярную оси Ох. Функцияs = s(х) получит приращение Δs, изображенного на рисунке в виде “пояска”.
Найдем дифференциал площади ds, заменяя образованную между сечениями фигуру усеченным конусом, образующая которого равна dl, а радиусы оснований равны у и у + dу. Площадь его боковой поверхности равнаds=  (у + у + dу) • d1 = 2
(у + у + dу) • d1 = 2  ydl +
ydl +  dydl.Отбрасывая произведение dу d1 как бесконечно малую высшего порядка, чем ds, получаем ds = 2
dydl.Отбрасывая произведение dу d1 как бесконечно малую высшего порядка, чем ds, получаем ds = 2  уdl, или, так как d1 =
уdl, или, так как d1 =  dx.
dx.
1.Интегрируя полученное равенство в пределах от х = а до х = b,получаем
S  = 2
= 2 
 y
y  dx.
dx.
Если кривая AB задана параметрическими уравнениями x = x(t), y = y(t), t  ≤ t
≤ t  ≤ t
≤ t  , то формула для площади поверхности вращения принимает вид
, то формула для площади поверхности вращения принимает вид
S  = 2
= 2  dt.
dt.
Пример 6.Найти площадь поверхности шара радиуса R.
Решение:Можно считать, что поверхность шара образована вращением полуокружности y =  , -R ≤ x ≤ R, вокруг оси Ox. По формуле S
, -R ≤ x ≤ R, вокруг оси Ox. По формуле S  = 2
= 2 
 y
y  dx находим S = 2
dx находим S = 2  =
=

Вычисление площадей плоских фигур.
Прямоугольные координаты
Пусть функция f(х) непрерывна на сегменте [а;b]. Если f(х )≥0 на [а; b]то площадь S криволинейной трапеции, ограниченной линиями у =f(х), у = 0, х = а, х = b, равна интегралу  Если же f(x) ≤ 0 на [а; b]то f(х) ≥ 0 на [а; b].Поэтому площадь S соответствующей криволинейной трапеции выразится формулой:
Если же f(x) ≤ 0 на [а; b]то f(х) ≥ 0 на [а; b].Поэтому площадь S соответствующей криволинейной трапеции выразится формулой:
 или
или 
Е  сли, наконец, кривая y=f(х) пересекает ось Ох, то сегмент [а;b]надо разбить на части, в пределах которых f(х) неменяет знака, и к каждой такой части применить ту из формул, которая ей соответствует.
сли, наконец, кривая y=f(х) пересекает ось Ох, то сегмент [а;b]надо разбить на части, в пределах которых f(х) неменяет знака, и к каждой такой части применить ту из формул, которая ей соответствует.
Пример 7.Найти площадь плоской фигуры, ограниченной параболой y = x2, прямыми х=1, х = 3 и осью Ох (рис. 9).
Решение: Пользуясь формулой  , находим искомую площадь S =
, находим искомую площадь S = 
Пример 8.Найти площадь плоской фигуры, ограниченной графиком функцииу = sinх и осью абсцисс при условии  (рис. 10).
(рис. 10).
Р  ешение:Разбиваем сегмент [0;
ешение:Разбиваем сегмент [0;  ] на два сегмента [0;
] на два сегмента [0;  ] и [
] и [  ; 2
; 2  ]. На первом из нихsinx ≥ 0, на втором sinx ≤ 0. Следовательно, используя формулы
]. На первом из нихsinx ≥ 0, на втором sinx ≤ 0. Следовательно, используя формулы  и
и  , имеем, что искомая площадь
, имеем, что искомая площадь 
Полярные координаты.
Пусть требуется определить площадь сектора ОАВ, ограниченного лучами  =
= 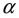 ,
,  =
=  и кривой АВ (рис. 11), заданной в полярной системе координат уравнением r = r (
и кривой АВ (рис. 11), заданной в полярной системе координат уравнением r = r (  ), где r (
), где r (  ) — функция, непрерывная на сегменте [
) — функция, непрерывная на сегменте [ 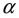 ;
;  ].
].
Р  азобьем отрезок [
азобьем отрезок [ 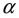 ;
;  ] на п частей точками
] на п частей точками
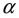 =
=  о<
о<  1 < ...<
1 < ...< 
 <
< 
 =
=  и положим: Δ
и положим: Δ  =
=  —
—  k = 1, 2, ..., n. Наибольшую из этих разностей обозначим через
k = 1, 2, ..., n. Наибольшую из этих разностей обозначим через  :
:  = max Δ
= max Δ  .
.
Разобьем данный сектор на п частей лучами  =
=  (k=1, 2, ..., п — 1). Заменим k-й элементарный сектор круговым сектором радиуса r(
(k=1, 2, ..., п — 1). Заменим k-й элементарный сектор круговым сектором радиуса r(  ), где
), где 
 .
.
Тогда сумма  - приближенно площадь сектора OAB. Отсюда:
- приближенно площадь сектора OAB. Отсюда:

Пример 9.Найти площадь плоской фигуры, ограниченной кардиоидой г =a(1+соs  ) (рис. 12).
) (рис. 12).
Решение:Учитывая симметричность кривой относительно полярной оси, по формуле  получаем:
получаем:



Дата добавления: 2018-02-28; просмотров: 282; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
