Вычисление и увязка приращений координат в замкнутых и разомкнутых теодолитных ходах
Обработка угловых измерений замкнутого полигона. Теоретическая сумма углов всякого плоского многоугольника равна 180°(n -2). Если фактическая сумма измеренных углов многоугольника ABCDEравна ∑β, то разность 
называют угловой невязкой полигона. Определив по величину угловой невязки полигона, ее необходимо сопоставить с величиной предельно допустимой невязки. Если fβ >fβпр, то все угловые измерения необходимо выполнить заново. Если fβ <fβ пр, то производят уравнивание (увязку) угловых измерений. При измерениях горизонтальных углов в теодолитных ходах техническими теодолитами предельную погрешность измерения одного угла принимают равной ±1,5', тогда предельная погрешность суммы n углов, очевидно, составит: 
Для трасс автомобильных дорог (разомкнутые теодолитные ходы) по действующим техническим нормам предельная допустимая невязка принята: 
Обработка угловых измерений разомкнутого теодолитного хода. Прежде всего необходимо установить соотношения между углами теодолитного хода и дирекционными углами соответствующих направлений.
т. е. дирекционный угол каждой последующей линии равен дирекционному углу предыдущей плюс 180°, минус вправо по ходу лежащий угол.
Если в выражении первую формулу для определения си подставить во вторую для определения, получим 
Теперь, подставив а2 в а3 и т. д., будем иметь 
окончательно получим 
|
|
|
Формула служит для контроля правильности вычисления дирекционных углов направлений разомкнутого теодолитного хода. Учитывая, что угловые измерения ведут с определенной погрешностью, из выражения можно определить невязку угловых измерений теодолитного хода: 
Уравнивание угловых измерений состоит в распределении полученной допустимой угловой невязки fβ поровну между всеми углами теодолитного хода с обратным знаком.
Прямая и обратная геодезические задачи.
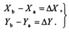Прямая геодезическая задача.Если линия АВ является одной из сторон теодолитного хода , для которой известна ее горизонтальная проекция d, дирекционный угол а и координаты первой точки А (Хa, Уа), то требуется определить координаты второй точки В (Хb, Уb).
Разности координат ∆Хи ∆У точек последующей и предыдущей называют приращениями координат. Приращения координат ∆Х и ∆У представляют собой проекции отрезка АВ на соответствующие оси координат.
Учитывая, что в выражениях величина горизонтальной проекции расстояния d всегда положительна, знаки приращений координат будут определяться только знаками соответствующих тригонометрических функций. При использовании в вычислениях таблицами тригонометрических функций необходимо перейти от дирекционных углов а к румбам r:
|
|
|
В связи с тем, что значения тригонометрических функций cosr и sinr всегда положительны (r< 90°), знаки приращений координат в выражениях определяют в соответствии с названиями четвертей румбов.
Определив по выражениям приращения координат ∆Х и ∆Y, находят искомые координаты другой точки:
Обратная геодезическая задача.Если на местности известны координаты двух точек А (Хa, Ya) и В (Хb, Уb), то можно определить горизонтальную проекцию расстояния между ними d и дирекционный угол a этого направления а. В соответствии с выражением имеем:
Посредством формул решают обратную геодезическую задачу, при этом горизонтальную проекцию расстояния d для контроля вычисляют дважды. В случае необходимости определения только горизонтальной проекции расстояния между двумя точками с известными координатами пользуются формулой:
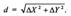
При вычислениях направлений с использованием таблиц тригонометрических функций по формулам сначала определяют румб направления: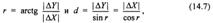 
а затем в соответствии с таблицей переходят от румбов к дирекционным углам. При решении прямой и обратной геодезических задач целесообразно пользоваться микрокалькуляторами, поскольку в этом случае отпадает необходимость вычисления румбов.
|
|
|
Дата добавления: 2018-02-28; просмотров: 1843; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!