Для широтно-импульсного регулирования
ОУ является компаратором, который сравнивает два сигнала - пилообразный и управляющий. Изменяя величину Uупр можно менять длительность интервалов t1 и t2. При этом период выходного сигнала T изменяться не будет, а соотношение между t1 и t2 будет зависеть от Uупр. Варианты:
1. Uупр=0: t1=0, t2=T, Uвых = -Uнас.
2. Uупр=Uпил.max/2: t1=t2=T/2, Uвых.ср.=0.
3. Uупр=Uпил.max : t1=T, t2=0, Uвых =Uнас.
Т.о. изменяя величину Uупр от 0 до max можно менять среднее значение выходного напряжения Uвых.ср. от -Uнас. до Uнас. Uвых.ср. - это постоянная составляющая выходного сигнала, которая может быть выделена с помощью фильтра. При изменении ширины интервалов t1 и t2 меняется Uвых.ср, поэтому такой способ регулирования среднего значения напряжения называется широтно-импульсное регулирование.
Триггер Шмитта на ОУ
Он является компаратором с зоной нечувствительности. Зона нечувствительности может быть установлена любая желаемая, например, такой величины, чтобы при определении знака входного сигнала не чувствовался уровень помех во входном сигнале.
Триггер Шмитта строится на основе компаратора, но добавляется положительная обратная связь. В этой схеме на неинвертирующий вход через делитель R1R2 подана часть выходного напряжения, причем знак напряжения на неинвертирующем входе зависит от знака выходного напряжения. Напряжение на неинвертирующем входе называют опорным
Uоп=Uвых´R2/(R1+R2).
Диаграммы работы представлены на рис.101. Иногда Uоп называют пороговым напряжением. Т.о., если полезный сигнал содержит уровень помех меньше Uоп, то эти помехи на определение знака не будут сказываться. Знак определяется только гладкой составляющей опорного сигнала. При отсутствии опорного сигнала при переходе входного сигнала через нуль и наличии помех было бы многократное переключение компаратора за счет помех.
Схема мультивибратора на ОУ
Мультивибратор является автоколебательной схемой. Выход мультивибратора изменяет свое состояние на противоположное за счет действия времязадающей RC цепи. Составной частью мультивибратора является схема триггера Шмитта. При изображении мультивибратора к триггеру Шмитта добавляют времязадающую RC цепь, которая действует на инвертирующий вход ОУ вместо источника внешнего входного сигнала.
Будем рассматривать работу мультивибратора с момента подачи питания в схему. При подаче питания выход примет значение +Uнас или -Uнас. В первый момент конденсатор С разряжен и напряжение между входами равно Uоп. При установке в исходное состояние конденсатор С начинает заряжаться. Между входами ОУ напряжение Uоп-Uс, т.к. Uоп>Uс, то Uоп определяет выход ОУ. Когда Uс достигнет Uоп, произойдет переключение ОУ на противоположное. В момент равенства этих напряжений ОУ начинает работать в соответствии с его свойствами. Т.к. при этом напряжение между входами близко к нулю и меняет знак на противоположный, то и выходное напряжение меняется на противоположное. При изменении знака выходного напряжения меняется знак опорного и конденсатор начинает перезаряжаться по пунктирной стрелке. Когда положительное напряжение на конденсаторе сравнивается с положительным опорным (момент времени t2), выходное напряжение ОУ изменится на противоположное.
При включении схемы интервал (0-t1) короче, чем последующие интервалы. Для установившегося режима:
t1=t2=t3=...; T=t1+t3ºR3C1; f=1/T.
Тема 4. ЦИФРОВЫЕ УСТРОЙСТВА
Анализ и синтез цифровых схем проводят на основе Булевой алгебры. Джон Буль - английский математик XIX века.
Цифровые схемы оперируют с логическими переменными, которые обозначаются буквами латинского алфавита. Над логическими переменными можно совершать 3 основных действия:
операция ИЛИ;
операция И;
операция НЕ.
ИЛИ - логическое сложение (дизъюнкция).
И - логическое умножение (конъюнкция).
НЕ - инверсия, отрицание.
Обозначение этих действий:
ИЛИ обозначается +,(V);
И обозначается ´,(/\);
НЕ обозначается чертой над логической переменной.
Основные свойства логических функций
Переменная, связанная логическими операциями, образует логическую функцию. Свойства логических функций:
1. Свойства логического сложения.
0+0=0;
0+1=1;
1+1=1.
2. Свойства логического умножения.
0´0=0;
0´1=0;
1´1=1.
3. Свойства отрицания.


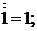

Приведенные соотношения называются аксиомами.
Основные свойства в общем виде:
а+0=а; а´0=0;
а+1=1; а´1=а; 
а+а=а; а´а=а;


Основные логические законы
1. Переместительный закон
a+b=b+a;
a×b=b×a.
2. Сочетательный закон
(a+b)+c=a+(b+c);
(a×b)×c=a×(b×c).
3. Распределительный закон
a×(b+c)=a×b+a×c;
a+(b×c)=(a+b)×(a+c).
Доказательство: a+bc=a(1+b+c)+bc=a+ab+ac+bc=a(a+c)+b(a+c)=(a+c)×(a+b).
4. Закон поглощения
a+ab=a(1+b)=a;
a×(a+b)=a+ab=a.
5. Закон склеивания


6. Закон отрицания (законы Моргана)


Законы Моргана позволяют реализовать функционально полные системы на элементах И-НЕ, ИЛИ-НЕ.
Дата добавления: 2018-02-28; просмотров: 311; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
