Задания к лабораторной работе. Лабораторная работа №2. Метод наименьших квадратов
Лабораторная работа №2. Метод наименьших квадратов
Пусть в результате некоторого эксперимента получены данные в виде чисел записанных в таблицу 2.1
Таблица 2.1
| 
| 
| 
| 
|
| 
| 
|
| 
|
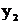
На основании этих данных требуется установить функциональную зависимость величины 
от величины 
: 
. Вид функции устанавливается обычно или из теоретических соображений, или визуально, исследуя расположение 
точек 
на плоскости 
.
Наиболее часто в качестве подбираемой функции используют следующие функции:
а) полином: 
;
б) дробно-рациональную: 
;
в) экспоненциальную: 
; (2.1)
г) логарифмическую и другие функции,
где 
числа, заранее неизвестные. И задача заключается именно в нахождении этих чисел.
Замечание:
1. Если нет никаких теоретических указаний о виде зависимости , то следует искать наиболее простую формулу, содержащую как можно меньшее количество параметров 
;
2. Полное совпадение с данными эксперимента и не желательно, т.к. определяемая функция будет повторять ошибки экспериментатора.
Существует много различных методов нахождения коэффициентов 
. Они излагаются в учебниках по численным методам математики, там же излагаются их достоинства и недостатки. Здесь будет рассмотрен один из этих методов - метод наименьших квадратов.
Итак, имеем 
функцию многих переменных, которая зависит от и еще нескольких неизвестных величин 
.
|
|
|
В методе наименьших квадратов коэффициенты 
ищутся из условия минимума суммы квадратов невязок
,
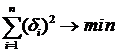где 
- невязка, которая порождена случайной ошибкой измерения.
Это условие имеет серьезное статистическое обоснование, так как ошибки измерения распределены по нормальному закону, то можно показать, что метод наименьших квадратов вытекает из метода максимального правдоподобия.
Составим новую функцию
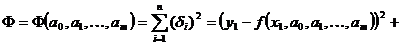
. (2.2)
Величины надо найти таким образом, чтобы функция 
имела наименьшее значение. Иными словами, отклонение экспериментальных точек от теоретической кривой должно быть минимальным.
Тогда по правилам математического анализа применяя необходимое
условие экстремума функции нескольких переменных, имеем:
. (2.3)
В результате получится система из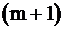 
линейного уравнения с 
неизвестными . В каждом конкретном случае исследуется вопрос о существовании решения этой системы, единственности этого решения и о наличии минимума функции при полученных значениях величин .
Рассмотрим частные случаи подбираемой функции .
1) Пусть 
полином 1-й степени, т.е.
|
|
|
. График этой функции есть прямая линия. В этом случае вспомогательная функция 
есть функция двух переменных и имеет вид:
. (2.4)
Тогда система (2.2) будет представлена следующими двумя уравнениями:
(2.5)
Теперь необходимо вычислить коэффициенты системы (значения 
и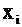 
даны в таблице 2.1). Обозначим
.
Тогда система (2.5) принимает вид:
(2.6)
Эта система из двух линейных уравнений с двумя неизвестными 
и 
. Решим систему по формулам Крамера:
.
Если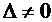 
, то решение существует и оно единственно, и это решение:
При найденных значениях и функция (2.4) имеет минимальное значение. Это доказывается, если вычислить 
при полученных 
и подставить в достаточные условия экстремума функции нескольких переменных.
ПРИМЕР 2.1 На основании некоторого эксперимента получены данные
Таблица 2.2
| хi | 1 | 2 | 3 | 5 |
| yi | 3 | 4 | 2,5 | 0,5 |
Нанесем эти значения на координатную плоскость (рисунок 2.1) и визуально исследуем расположение точек. В данном случае можно допустить линейную зависимость величины 
от величины , т.е. 
. Строим вспомогательную функцию
|
|
|
Рисунок 2.1
и тогда система (2.5) имеет вид:
(2.7)
Вычислим коэффициенты 
:
Подставим в систему (2.7):
Итак: 
В результате получаем функцию 
.
Для анализа полученного уравнения составим таблицу 2.3
Таблица 2.3
| xi | yi | 
| 
| 
|
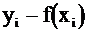
| 1 | 3,0 | 3,797 | - 0,797 | 0,635 |
| 2 | 4,0 | 3,054 | 0,946 | 0,895 |
| 3 | 2,5 | 2,311 | 0,189 | 0,0324 |
| 5 | 0,5 | 0,825 | - 0,325 | 0,105 |
Минимальное значение функции 
при найденных коэффициентах
равно:
.
Если коэффициенты 
хотя бы немного изменить, то значение функции будет увеличиваться.
2) Пусть 
полином 2-й степени, т.е. 
график этой функции есть парабола. В этом случае вспомогательная функция 
есть функция трех переменных и имеет вид:
(2.8)
Тогда система (2.3) будет представлена тремя уравнениями:
(2.9)
Теперь необходимо вычислить коэффициенты этой системы (значения 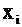и даны в таблице 2.1):
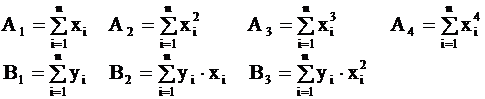
С использованием этих чисел система (2.9) принимает вид:
(2.10)
Эта система из трех линейных уравнений с тремя неизвестными 
, 
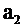. Решим систему по формулам Крамера:
Если 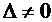, то система (2.10) имеет единственное решение:
|
|
|
.
При найденных значениях , 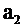функция (2.8) имеет минимальное значение. Это доказывается с использованием достаточных условий экстремума функции нескольких переменных.
ПРИМЕР 2.2 В результате эксперимента получены числовые данные, записанные в виде таблицы 2.4
Таблица 2.4
| х | 2 | 3 | 4 | 5 | 6 |
| y | 0,2 | 3,0 | 4,2 | 2,8 | 0,5 |
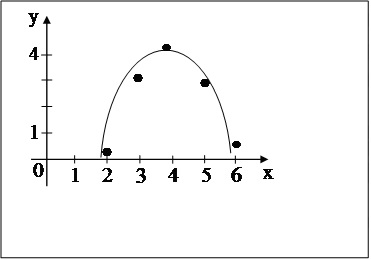
Рисунок 2.2
Нанесем эти данные на координатную плоскость, исследуем расположение точек и видим, что зависимость величины от величины можно описать параболой, т.е. 
. Строим вспомогательную функцию: 
и тогда система (2.9) имеет вид:
(2.11)
Теперь необходимо вычислить коэффициенты этой системы:
Подставим полученные значения в систему (2.11) или в систему (2.10):
Решаем эту систему линейных уравнений методом Крамера:
.
В результате получаем функцию 
.
Для анализа полученного уравнения составим таблицу 2.5
Таблица 2.5
| xi | yi |
|
|
|
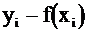
| 2 | 0,2 | 0,24 | - 0,04 | 0,0016 |
| 3 | 3,0 | 3,04 | - 0,04 | 0,0016 |
| 4 | 4,2 | 4,02 | 0,18 | 0,0324 |
| 5 | 2,8 | 3,18 | - 0,02 | 0,0002 |
Минимальное значение функции при найденных коэффициентах
равно:
.
Если коэффициенты 
хотя бы немного изменить, то значение функции будет увеличиваться.
3) Пусть экспоненциальная функция, а именно 
. В этом случае, при решении системы (2.3), возникают трудности, которые, однако, можно преодолеть линеаризацией уравнения 
. Логарифмируем его: 
. Обозначим 
, тогда имеем 
это линейное уравнение. Если найдем его коэффициенты, то исходные коэффициенты рассчитаем по формулам 
.
ПРИМЕР 2.3 В результате эксперимента получены данные, выписанные в виде таблицы 2.6:
Таблица 2.6
| xi | - 1 | 0 | 1 | 2 | 3 |
| yi | 6 | 2 | 7/9 | 1/3 | 1/10 |
Нанесем эти данные на координатную плоскость (рисунок 2.3), исследуем расположение точек и видим, что лучше всего зависимость
Рисунок 2.3
величины от величины описывается экспоненциальной функцией:
. Поскольку в данном случае 
, то прологарифмируем уравнение: 
, сделаем обозначения 
;
; 
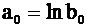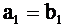и получаем линейное уравнение 
. (2.12)
Для нахождения коэффициентов у последнего уравнения, воспользуемся изложенной выше теорией и обратимся к примеру 2.1.
Таблица 2.7
| xi | - 1 | 0 | 1 | 2 | 3 |
| yi | 6 | 2 | 7/9 | 1/3 | 1/10 |
| zi | 
| 
| 
| 
| 
|
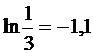
Строим вспомогательную функцию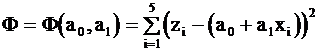 
. Система (2.5) имеет вид в этом случае:
(2.13)
Вычислим коэффициенты :
.
Подставим в систему (2.13):
, 
.
Возвращаемся к коэффициентам 
и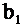 
. Так как 
, то найдем искомые коэффициенты: 
, а также получим функцию 
.
Для анализа полученного уравнения составим таблицу 2.8
Таблица 2.8
| xi | yi |
|
| 
|
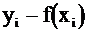
| - 1 | 6 | 5,848 | 0,152 | 0,023 |
| 0 | 2 | 2,15 | - 0,15 | 0,0225 |
| 1 | 
| 0,79 | - 0,012 | 0,000144 |
| 2 | 
| 0,29 | 0,039 | 0,0015 |
| 3 | 
| 0,107 | - 0,007 | 0,00005 |
Минимальное значение функции при найденных коэффициентах равно:
Задания к лабораторной работе
В результате эксперимента получены данные, выписанные в виде таблицы. Методом наименьших квадратов требуется установить функциональную зависимость величины от величины :
| Вариант | 1 |
|
|
|
|
|
| x | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 |
| y | 0,5 | 7,5 | 12,5 | 14,5 | 14,5 | 15 |
|
|
|
|
|
|
|
|
| Вариант | 2 |
|
|
|
|
|
| x | -0,5 | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 |
| y | 10,5 | 9,5 | 6,5 | 4,5 | 2,5 | 2,5 |
|
|
|
|
|
|
|
|
| Вариант | 3 |
|
|
|
|
|
| x | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 |
| y | 0,5 | 3,5 | 4,5 | 4,5 | 4,5 | 4 |
|
|
|
|
|
|
|
|
| Вариант | 4 |
|
|
|
|
|
| x | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 |
| y | 0,5 | 5,5 | 6,5 | 8,5 | 9,5 | 9 |
|
|
|
|
|
|
|
|
| Вариант | 5 |
|
|
|
|
|
| x | -0,5 | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 |
| y | 9,5 | 7,5 | 5,5 | 6,5 | 6,5 | 6,5 |
|
|
|
|
|
|
|
|
| Вариант | 6 |
|
|
|
|
|
| x | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 | 8,5 |
| y | 0,5 | 6,5 | 12,5 | 14,5 | 15,5 | 15 |
|
|
|
|
|
|
|
|
| Вариант | 7 |
|
|
|
|
|
| x | -2,5 | -1,5 | -0,5 | 0,5 | 1,5 | 2,5 |
| y | 0,5 | 1,5 | 2,5 | 2,5 | 2,5 | 4 |
|
|
|
|
|
|
|
|
| Вариант | 8 |
|
|
|
|
|
| x | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 |
| y | 10,5 | 10,5 | 9,5 | 9,5 | 6,5 | 7,5 |
|
|
|
|
|
|
|
|
| Вариант | 9 |
|
|
|
|
|
| x | 4,5 | 5,5 | 6,5 | 7,5 | 8,5 | 9,5 |
| y | 0,5 | 3,5 | 8,5 | 8,5 | 9,5 | 10 |
|
|
|
|
|
|
|
|
| Вариант | 10 |
|
|
|
|
|
| x | -1,5 | -0,5 | 0,5 | 1,5 | 2,5 | 3,5 |
| y | 9,5 | 9,5 | 8,5 | 7,5 | 6,5 | 7,5 |
|
|
|
|
|
|
|
|
| Вариант | 11 |
|
|
|
|
|
| x | -1,5 | -0,5 | 0,5 | 1,5 | 2,5 | 3,5 |
| y | 0,5 | 4,5 | 5,5 | 5,5 | 6,5 | 8 |
|
|
|
|
|
|
|
|
| Вариант | 12 |
|
|
|
|
|
| x | -2,5 | -1,5 | -0,5 | 0,5 | 1,5 | 2,5 |
| y | 9,5 | 9,5 | 9,5 | 5,5 | 6,5 | 8 |
| Вариант | 13 |
|
|
|
|
 Мы поможем в написании ваших работ! | |||||||||||