ПРОГНОЗИРОВАНИЕ КОЛИЧЕСТВА АВАРИЙ НА УЧАСТКАХ МАГИСТРАЛЬНЫХ ГАЗОПРОВОДОВ С ОПАСНЫМИ ДЕФЕКТАМИ
Газопровод Уренгой-Челябинск, классификация аварий,
Время эксплуатации, прогнозирование дефектных секций
Gas pipeline Urengoi-Chelyabinsk, emergencies classification, operation time, defective sections prediction
UDC 622.691:620
Prediction of quantity of emergences in the trunk gas pipeline sections with critical defects.Malyushin N.A., Minyailo I.V.
The results of diagnostic survey of the trunk gas pipeline Urengoi-Chelyabinsk are presented. A formula was obtained for determination of defective sections of linear runs of pipelines. A comparison of actual and predicted data showed a good convergence of results. The error was only 0.2%. The formula obtained makes it possible to predict with high accuracy a presence of defective sections preventing the emergency situations.Fig. 1,Table 1.
| Р |
езультаты диагностического обследования линейных участков магистрального газопровода Уренгой-Челябинск позволяют оценить их техническое состояние и определить безопасные режимы перекачки газа или установить очередность ликвидации опасных дефектов, одновременно спрогнозировав остаточный ресурс сооружения.
Анализ результатов обследования ряда нефте- и газопроводов показывает, что за последние 20 лет основными видами дефектов и аварий являются коррозионные повреждения металла труб. Встречаются так же механические повреждения, связанные с работой ремонтной техники на трассах. Брак строительно-монтажных работ в основном выявлен в интервале начальных 10-ти лет эксплуатации. Классификация аварий линейной части осуществляется по различным признакам. При построении модели выделяют две группы причин: внешние и внутренние. Внешние причины включают условия прокладки, свойства транспортируемой среды, режимы перекачки и т.п., то есть причины, являющиеся постоянными при эксплуатации, а внутренние – причины, зависящие от времени эксплуатации. При такой классификации дефектов можно использовать для анализа динамики отказов секций трубопроводов вероятностную модель отказов. Принимаем, что все секции находятся в одинаковых условиях эксплуатации, что позволяет использовать аппарат формально-кинетического анализа и представить функцию отказов в виде следующего дифференциального уравнения:
|
|
|
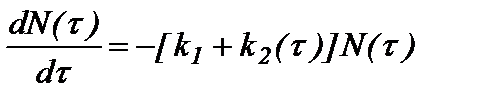, (1)
где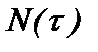 
– число работоспособных секций трубопровода; 
– коэффициент, учитывающий влияние на отказ секций трубопроводов причин первой группы (условия прокладки, режимы работы и т.п.);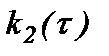 
– коэффициент, учитывающий влияние второй группы (коррозийные повреждения металла труб), зависящие от времени эксплуатации. Следовательно, коэффициент 
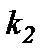будет отражать увеличение вероятности отказов, связанных с изменением свойств материала, а в качестве основного принимаются коррозионные повреждения. Коэффициент 
, исходя из предложенных моделей коррозионного повреждения, можно представить в виде
|
|
|
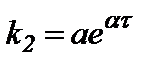, (2)
где 
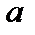и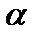 
– эмпирические коэффициенты. Сопоставление уравнений (1) и (2) позволяют преобразовать уравнение (1) и представить его в виде
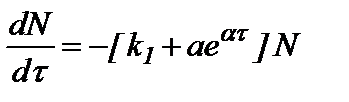. (3)
Для начала эксплуатации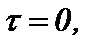 
тогда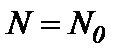 
– число секций рассматриваемого участка газопровода, шт. Тогда
, (4)
то есть закон изменения отказов секций газопровода, так же как и коррозионные повреждения, оказывается экспоненциальным. В этом случае основной задачей является определение эмпирических коэффициентов предложенной модели. Они могут быть определены следующим образом с введением обозначений:
(a)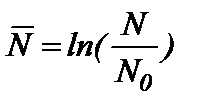 
, (б)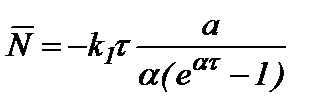 
.
Эту функцию можно разложить в ряд Тэйлора:
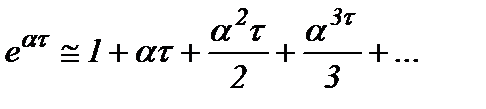. (5)
Исходя из анализа рассмотренного ряда и учитывая, что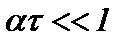 
, можно ограничиться тремя членами ряда, тогда
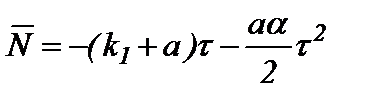. (6)
Коэффициенты в уравнении (6) можно определить, располагая данными о количестве отказов труб в фиксированные отрезки времени от начала эксплуатации. Это позволяет записать для их определения систему нелинейных уравнений:
;
;
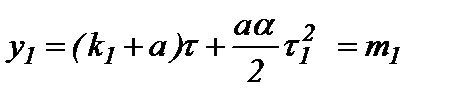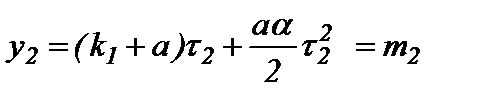…………………………………….. (7)
|
|
|
.
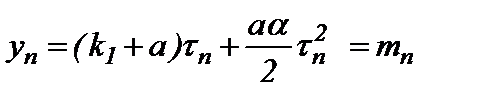В этом случае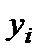 
и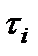 
- фактические данные по количеству отказов секций труб (их замене) в интервале времени 
. Обозначим 
, 
.
Запишем для расчета эмпирических коэффициентов условную функцию вида
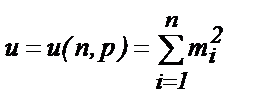. (8)
Получим
. (9)
Минимумы функций позволяют определить требуемые коэффициенты из следующих уравнений:
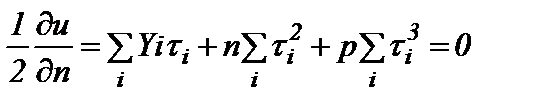, (10а)
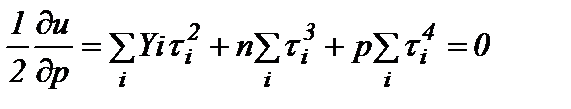. (10б)
Преобразуем полученные уравнения (10а) и (10б):
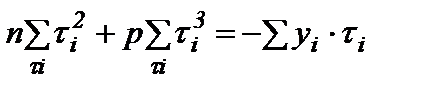, (а)
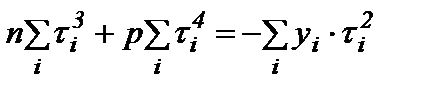. (б)
На основании теоремы Крамера, решая полученные уравнения, имеем следующее:
= 
,
= 
,
= 
.
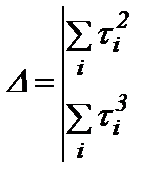
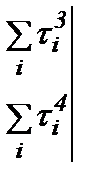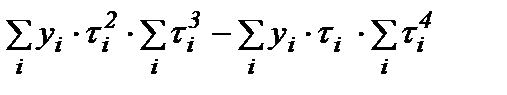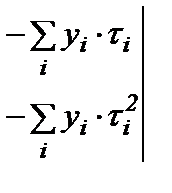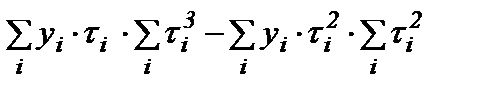Окончательно получаем уравнения для расчета эмпирических коэффициентов:
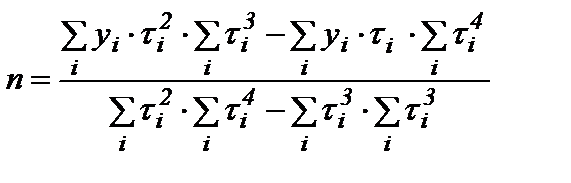, (11)
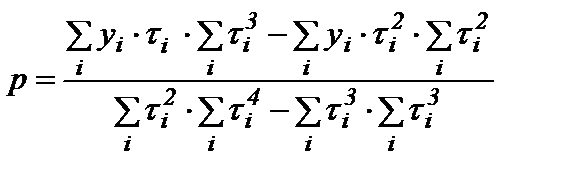. (12)
Вычисление коэффициентов n u p осуществляется по известным значениям числа отказов для фиксированных значений времени 
, в качестве которых принимаем интервалы времени эксплуатации от начала ее до момента двух последовательных диагностических обследований. В качестве расчетных значений принимаем интервалы времени 
=19лет и 
=23года (время проведения диагностических обследований).
|
|
|
Получим уравнение по расчету числа поврежденных секций с течением времени, что позволяет рассчитать число поврежденных секций при последующей эксплуатации и заранее резервировать необходимое их число для капитального ремонта, а также позволяет поддерживать надежность линейной части на проектном уровне (рис. 1).
Решение полученного уравнения имеет вид
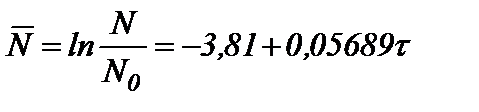. (13)
| Количество секций |
| Время эксплуатации |
|
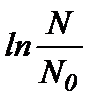
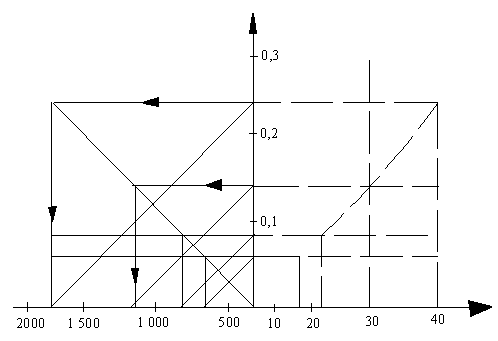
Приведено сопоставление фактических и расчетных значений числа секций с прогнозом их повреждений до 50 лет эксплуатации (таблица).
Дата добавления: 2018-02-28; просмотров: 309; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!