Определение момента инерции физического маятника в зависимости от распределения массы

Nbsp; Лабораторная работа №5 по курсу общей физики.   Определение моментов инерции тел произвольной формы.   Выполнил: Усманов К.Р. ИИТ-125

Цель работы

Определение момента инерции математического и физического маятников.

Теоретическая часть

Математическим маятником называется материальная точка, подвешенная на невесомой нерастяжимой нити.

Период колебания математического маятника определяется по формуле:

                                                               ,                                                        (2.1)

где l – длина нити.

Физическим маятником называется твердое тело, способное совершать колебания вокруг неподвижной оси, не совпадающей с его центром инерции. Колебания математического и физического маятников происходят под действием квазиупругой силы, которая является одной из составляющих силы тяжести.

Пусть дан физический маятник произвольной формы, центр инерции которого находится в точке С (рис. 2.1). Отклоним маятник на некоторый угол j от вертикали. Одна из составляющих силы тяжести  создает вращательный момент M, который стремится вернуть маятник в положение равновесия.

                                                      ,                                              (2.2)

где m – масса маятника;

l – расстояние между точкой подвеса и центром инерции маятника.

Согласно 2 закону Ньютона, для вращательного движения

                                                                 ,                                                         (2.3)

где I – момент инерции;

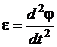 - угловое ускорение.

                                                         .

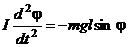При малых углах колебаний , тогда

                                                            .                                                    (2.4)

Уравнение (2.4) можно переписать в виде

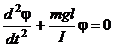                                                                                                              (2.5)

или

                                                            ,                                                    (2.6)

где .

Решение этого уравнения имеет вид

                                                         ,                                                  (2.7)

где a и a - произвольные постоянные.

Зная w₀, можно рассчитать период колебаний T физического маятника:

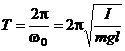                                                                                                            (2.9)

Приведенной длиной физического маятника называется длина такого математического маятника, у которого период колебаний совпадает с периодом колебаний физического маятника.

                                                                                                                          (2.10)

Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения O, называется центром качанияфизического маятника O¢.

По теореме Штейнера момент инерции тела относительно любой оси

                                                              ,                                                     (2.11)

где I₀ – момент инерции тела относительно оси, проходящей через центр тяжести;

l – расстояние между осями.

Подставим в уравнение (2.10) момент инерции из выражения (2.11):

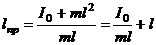                                                     .                                            (2.12)

Зная период колебания T, массу маятника m и приведенную длину, можно рассчитать момент инерции I физического маятника:

                                                      .                                             (2.14)

Расчет погрешностей

                                                                                                                      (2.15)

Используя формулу

                                                                      (2.16)

вычисляю абсолютную погрешность DI:

                                     ,                           (2.17)

где Dm = 0,001 кг.

Dl = 0,001 м.

DT = 0,01 с.

Относительная погрешность рассчитывается по формуле:

                                                                                                                            (2.18)

Экспериментальная часть

Определение моментов инерции математического и физического маятников.

№	m, кг	l, м	n	t, с	Tм, с	g, м/с2	Iм, кг×м2
1	0,115	0,448	30,000	40,700	1,357	9,609	0,023
2				40,700	1,357	9,609	0,023
3				40,500	1,350	9,704	0,023

 

№	mф, кг	n	t, с	Tф, с	l, м	Iф, кг×м2	DI, кг×м2	e, %
1	2,000	30,000	40,300	1,343	0,385	0,345	0,004	1,054
2			40,300	1,343	0,385	0,345	0,004	1,054
3			40,400	1,347	0,385	0,347	0,004	1,052

 

I_ф = 0,346 ± 0,004 кг×м²

Определение момента инерции физического маятника в зависимости от распределения массы.

№		n	t, с	T, с	l, м	I, кг×м2	DI, кг×м2
1	1	30,000	40,300	1,343	0,385	0,345	0,004
	2		40,300	1,343	0,385	0,345	0,004
	3		40,400	1,347	0,385	0,347	0,004
2	1	30,000	37,100	1,237	0,315	0,239	0,003
	2		37,000	1,233	0,315	0,238	0,003
	3		36,900	1,230	0,315	0,237	0,003
3	1	30,000	34,100	1,137	0,265	0,170	0,002
	2		34,100	1,137	0,265	0,170	0,002
	3		34,100	1,137	0,265	0,170	0,002
4	1	30,000	31,700	1,057	0,220	0,122	0,002
	2		31,600	1,053	0,220	0,121	0,002
	3		31,800	1,060	0,220	0,123	0,002
5	1	30,000	30,700	1,023	0,165	0,086	0,001
	2		30,500	1,017	0,165	0,085	0,001
	3		30,600	1,020	0,165	0,085	0,001

Iф

кг×м2

l м

I_ф1 = 0,346 ± 0,004 кг×м²

I_ф2 = 0,238 ± 0,003 кг×м²

I_ф3 = 0,170 ± 0,002 кг×м²

I_ф4 = 0,122 ± 0,002 кг×м²

I_ф5 = 0,085 ± 0,001 кг×м²

 

Вывод: В данном опыте было установлено, что момент инерции физического маятника находится в сложной нелинейной зависимости от расстояния от точки подвеса до центра инерции.

 

---

Дата добавления: 2018-02-28; просмотров: 8217; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!