Разложение по формуле Маклорена некоторых элементарных функций
⇐ ПредыдущаяСтр 4 из 4
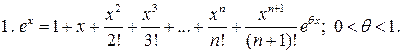

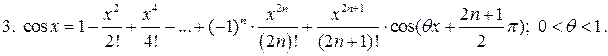
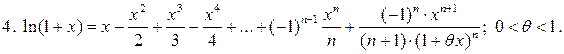
5. 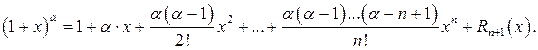
Частный случай 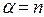 :
:
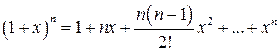 - формула бинома Ньютона.
- формула бинома Ньютона.
Приближенное значение функций:
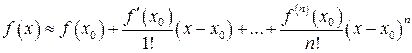 ,
,
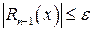 , где
, где 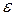 - погрешность.
- погрешность.
| пп 12. Теоретические Упражнения | ||
| ТУ ПП 12 №1 | Представьте функцию 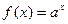 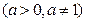 в виде многочлена третьей степени относительно в виде многочлена третьей степени относительно 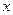 .
Решение: .
Решение:
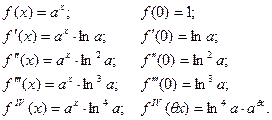 По формуле Маклорена получаем:
По формуле Маклорена получаем:
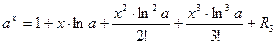 ,
где ,
где 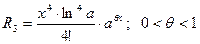 . .
| |
| ТУ ПП 12 №2 | Выяснить происхождение приближенных равенств
а) 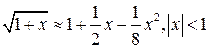 ;
б) ;
б) 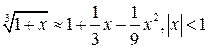 .
Решение:
Равенства получаются из разложения функции .
Решение:
Равенства получаются из разложения функции 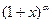 по формуле Маклорена с точностью до слагаемых второго порядка: по формуле Маклорена с точностью до слагаемых второго порядка:
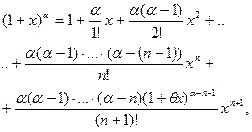
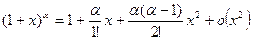
| |
| ТУ ПП 12 №3 | Функция 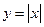 непрерывна, имеет на концах отрезка [-1,1] равные значения (проверьте!). Какова причина нарушения теоремы Ролля?
Решение: непрерывна, имеет на концах отрезка [-1,1] равные значения (проверьте!). Какова причина нарушения теоремы Ролля?
Решение:
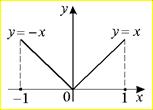 Для функции Для функции 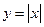 по определению не существует по определению не существует 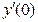 , так как , так как 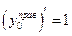 , , 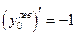 . .
| |
| пп 12. Дифференциал | ||
| ПП 12. №1. | Найдите дифференциал функции  при произвольном значении аргумента при произвольном значении аргумента 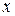 и при произвольном его приращении и при произвольном его приращении 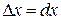 .
РЕШЕНИЕ: .
РЕШЕНИЕ:
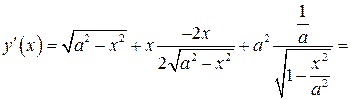  , , 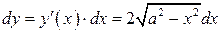 . .
| 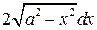
|
| ПП 12. №2. | Найдите дифференциал 2-го порядка функции 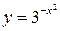 .
РЕШЕНИЕ: .
РЕШЕНИЕ:
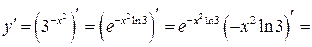 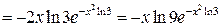 . . 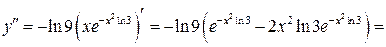 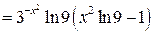 . .
| 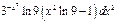
|
| ПП 12. №3. | Найдите дифференциал неявно заданной функции 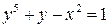 .
РЕШЕНИЕ:
Дифференцируем равенство: .
РЕШЕНИЕ:
Дифференцируем равенство: 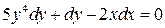 , откуда , откуда 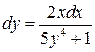 . .
| 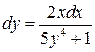
|
| ПП 12. №4. | Вычислите приближенное значение 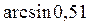 с помощью дифференциала.
Решение:
Рассмотрим функцию с помощью дифференциала.
Решение:
Рассмотрим функцию 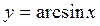 . Полагая . Полагая 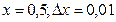 и применяя формулу и применяя формулу 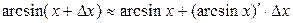 , получаем , получаем
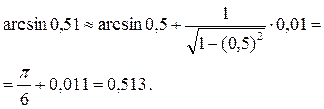
| 0,513 |
| ПП 12. №5. | Вычислите приближенно 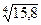 .
Решение:
Пусть .
Решение:
Пусть 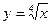 , где , где 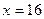 .
Тогда .
Тогда 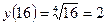 ; ;
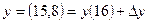 .
Применим формулу .
Применим формулу 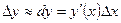 ; ;
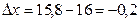 ; ;
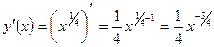 ; ;
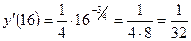 .
Тогда .
Тогда  . .
| 1,9938 |
| ПП 12. №6. | Вычислите приближенно значение объема  шара радиуса шара радиуса  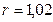 м.
Решение:
Так как м.
Решение:
Так как 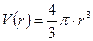 , то, полагая, , то, полагая, 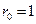 , ,  и используя формулу для и используя формулу для 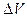 , получаем , получаем
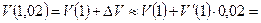 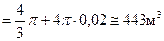 . .
|
Замечание. Здесь некоторые задачи ПП № 9 решены с помощью правила Лопиталя.
| пп 12. пРАВИЛО лОПИТАЛЯ | ||
| ПП 12. №7. | Раскройте неопределенность вида 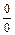 .
Решение: .
Решение:
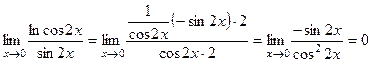 . .
| |
| ПП 12. №8. | Вычислите предел функции 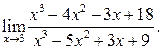 Решение:
Решение:
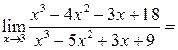 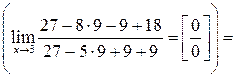 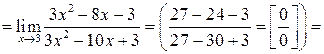 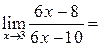 . . 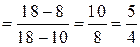 . .
| 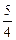
|
| ПП 12. №9. | Вычислите предел функции 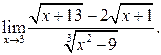 Решение:
Решение:
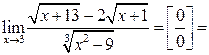 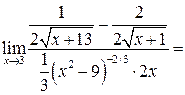 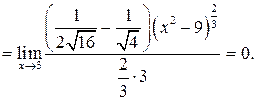
| |
| ПП 12. №10. | Вычислите предел функции 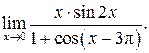 Решение:
Решение:
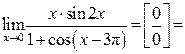 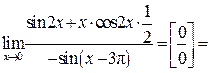 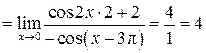 . .
| |
| ПП 12. №11. | Вычислите предел функции 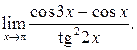 Решение:
Решение:
 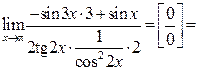 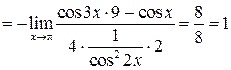 . .
| |
| ПП 12. №12. | Вычислите предел функции 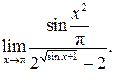 Решение:
Решение:
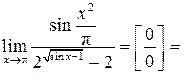 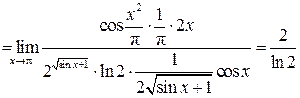 . .
| 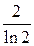
|
| ПП 12. №13. | Вычислите предел функции 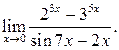 Решение:
Решение:
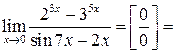 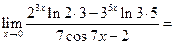 
| 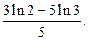
|
| ПП 12. №14. | Вычислите предел функции 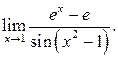 Решение:
Решение:
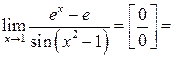 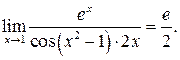
| 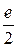
|
| ПП 12. №15. | Раскройте неопределенность вида 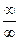 при вычислении предела последовательности: при вычислении предела последовательности:
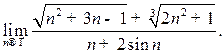 Решение:
Решение:
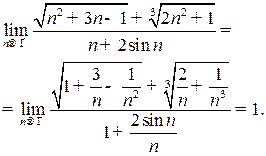
| |
| ПП 12. №16. | Раскройте неопределенность типа 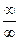 .
Решение: .
Решение:
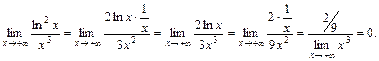 (Здесь правило Лопиталя применялось дважды).
(Здесь правило Лопиталя применялось дважды).
| |
| ПП 12. №17. | Раскройте неопределенность типа 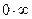
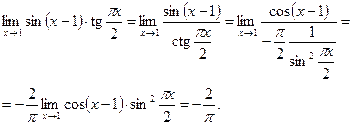
| 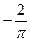
|
| ПП 12. №18. | Вычислите предел 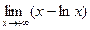 .
Решение:
Имеем неопределенность типа .
Решение:
Имеем неопределенность типа 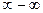 . .
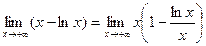 .
Исследуем .
Исследуем 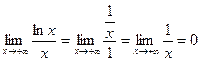 .
Таким образом, исходный предел .
Таким образом, исходный предел 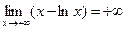 . .
| 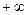
|
| ПП 12. №19. | Вычислите предел:  .
Решение:
Предел является неопределенностью типа .
Решение:
Предел является неопределенностью типа 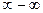 . Преобразуем: . Преобразуем:
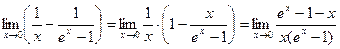 .
Дважды применяем правило Лопиталя. .
Дважды применяем правило Лопиталя.
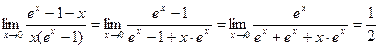 . .
| 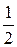
|
| ПП 12. №20. | Вычислите 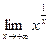 .
Решение:
Имеем неопределенность типа .
Решение:
Имеем неопределенность типа 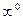 .P .P
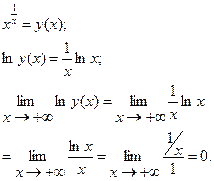 Тогда
Тогда 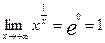 . .
| |
| ПП 12. №21. | Вычислите предел 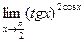 .
Решение:
Это неопределенность вида .
Решение:
Это неопределенность вида 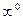 .
Положим .
Положим 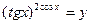 ; логарифмируем: ; логарифмируем: 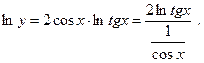 Применяя правило Лопиталя, получим:
Применяя правило Лопиталя, получим:
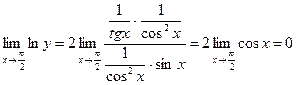 .
Таким образом, .
Таким образом, 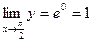 . .
|
| пп 12. фОРМУЛА ТЕЙЛОРА | ||||
| ПП 12. №22. | Многочлен  разложите по степеням разложите по степеням 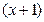 .
Решение: .
Решение:
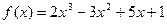 ; ; 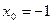 ; ; 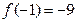 .
Найдем коэффициенты многочлена Тейлора: .
Найдем коэффициенты многочлена Тейлора:
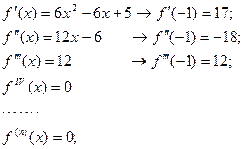
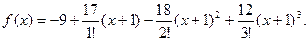 Учитывая, что
Учитывая, что 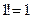 ; ; 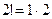 ; ; 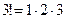 , получим , получим
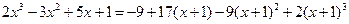 . .
| 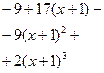
| ||
| ПП 12. №23. | Запишите формулу Маклорена n – го порядка для функции 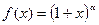 .
Решение: .
Решение:
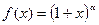 ; ; 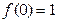 ; ; 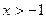 . .
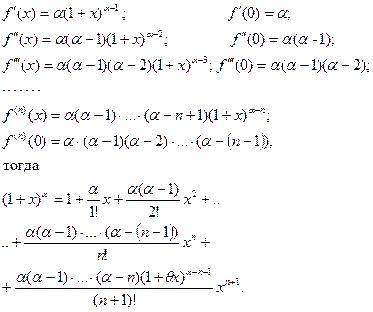
| 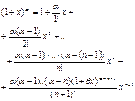
| ||
| ПП 12. №24. | Используя формулы Маклорена для элементарных функций, напишите первые n членов формулы Маклорена для функции 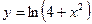 .
Решение:
Преобразуем исходную функцию: .
Решение:
Преобразуем исходную функцию:
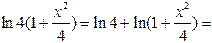
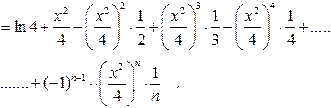 Окончательно:
Окончательно:
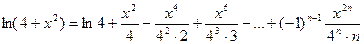 . .
| 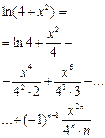
| ||
| ПП 12. №25. | Вычислите число e с точностью до 0,001.
Решение:
Запишем формулу Маклорена для e P x P:
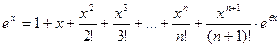 .
При .
При 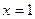 : :
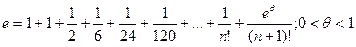 .
Наименьшее значение .
Наименьшее значение  , удовлетворяющее условию , удовлетворяющее условию 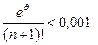 , равно 6, , равно 6, 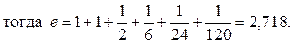
| 2,718 | ||
| ПП 12. №26. | Вычислите с точностью до 10P – 3P приближенное значение 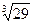 .
Решение:
Представим заданный корень так: .
Решение:
Представим заданный корень так: 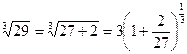 . Воспользуемся формулой Маклорена: . Воспользуемся формулой Маклорена:
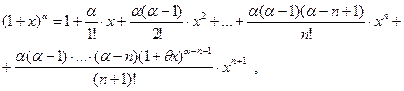 где последнее слагаемое представляет собой погрешность вычисления.
Полагая где последнее слагаемое представляет собой погрешность вычисления.
Полагая 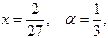 получим
получим
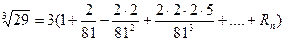 .
Оценивая величины последовательных ошибок в вычислении .
Оценивая величины последовательных ошибок в вычислении  , находим: , находим:
 Следовательно, для вычисления с заданной точностью достаточно взять три члена, которые предшествуют остатку R B 2 B, т.е.
Следовательно, для вычисления с заданной точностью достаточно взять три члена, которые предшествуют остатку R B 2 B, т.е.
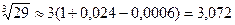 . .
| 3,072 | ||
| ПП 12. №27. | Используя разложение по формуле Маклорена, вычислите предел 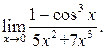 Решение:
Решение:
 ;
C точностью до бесконечно малых о ;
C точностью до бесконечно малых о 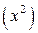 получаем: получаем:
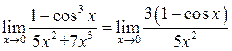 .
Заменим .
Заменим 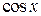 его разложением по формуле Маклорена: его разложением по формуле Маклорена:
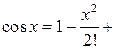 о о 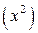 , тогда , тогда
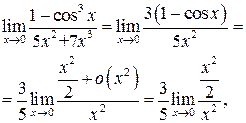 Поскольку
Поскольку 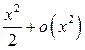 ~ ~  при при 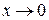 .
Окончательно .
Окончательно  . .
| 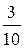
| ||
Дата добавления: 2015-12-21; просмотров: 25; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
