Свойства подмножеств
 (рефлексивность);
(рефлексивность);
 и
и  (транзитивность).
(транзитивность).
Прямое произведение множеств
Прямым (декартовым) произведением А1  А2
А2  …
…  Аn множеств А1, А2 … и Аn называется множество {< a1, a2, …, an > | a1
Аn множеств А1, А2 … и Аn называется множество {< a1, a2, …, an > | a1  A1, a2
A1, a2  A2,, an
A2,, an  An }, а An обозначает А
An }, а An обозначает А  А
А  …
…  А (n раз) и называется прямой степенью множества А.
А (n раз) и называется прямой степенью множества А.
Отношения
Бинарным отношением между элементами множеств А и В называется любое подмножество R множества А  В. Вместо < x, y >
В. Вместо < x, y >  R часто пишут xRy.
R часто пишут xRy.
Областью определения бинарного отношения R называется множество
d R = { x | существует y такое, что < x, y >  R }.
R }.
Областью значений бинарного отношения R называется множество
r R = { x | существует y такое, что < y, x >  R }.
R }.
Обратным отношением для бинарного отношения R называется множество
R-1 = {< x, y > | < y, x >  R }.
R }.
Образом множества Х относительно R называется множество
R (X) = { y | существует х  Х такое, что < x, y >
Х такое, что < x, y >  R },
R },
прообразом Х относительно R называется R-1 (X).
Произведением подмножеств R1 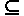 А
А  В и R2
В и R2 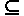 B
B  C называется отношение
C называется отношение
R1R2 = {< x, y > | существует z такое, что < x, z >  R1, < z, y >
R1, < z, y >  R2 }.
R2 }.
Свойства отношений
Бинарное отношение R на множестве А называется
· рефлексивным, если < x, х >  R для всех x
R для всех x  А;
А;
· симметричным, если < x, у >  R
R  < y, x >
< y, x >  R;
R;
· антисимметричным, если < x, у >  R и < y, x >
R и < y, x >  R
R  х = у;
х = у;
· транзитивным, если < x, у >  R и < y, z >
R и < y, z >  R
R  < x, z >
< x, z >  R.
R.
Рефлексивное, симметричное и транзитивное отношение на множестве А называется эквивалентностью на А. Классом эквивалентности (смежным классом) элемента х по эквивалентности R называется множество
|
|
|
[ x ] R = x / R = { y | < x, у >  R }.
R }.
Множество классов эквивалентности элементов множества А по эквивалентности R называется фактор-множеством А по R и обозначается А / R.
Бинарное отношение на множестве А называется предпорядком на А, если оно рефлексивно и транзитивно. Рефлексивное, антисимметричное, транзитивное отношение на множестве А называется частичным порядком на А ( ).
).
Частичный порядок  на множестве А называется полным на А, если каждое непустое подмножество А имеет наименьший элемент. Тогда А называется вполне упорядоченным.
на множестве А называется полным на А, если каждое непустое подмножество А имеет наименьший элемент. Тогда А называется вполне упорядоченным.
Функции
Отношение f называется функцией из А в В (из А на В), если d f = A, r f 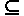 В (r f = В) и для всех x, y1, y2 из < x, y1 >
В (r f = В) и для всех x, y1, y2 из < x, y1 >  f и < x, y2 >
f и < x, y2 >  f следует y1 = y2. Обозначение f: A
f следует y1 = y2. Обозначение f: A  B. Пишем y = f (x) вместо < x, y >
B. Пишем y = f (x) вместо < x, y >  f и называем y значением функции f при значении аргумента х.
f и называем y значением функции f при значении аргумента х.
Функция f: A  B осуществляет взаимно однозначное соответствие межу А и В, если d f = A, r f= В и из того, что y = f (x1), y = f (x2) следует х1 = х2.
B осуществляет взаимно однозначное соответствие межу А и В, если d f = A, r f= В и из того, что y = f (x1), y = f (x2) следует х1 = х2.
Пусть А и В – частично упорядоченные множества и f – функция из А в В. f называется монотонным отображением, если из х1  х2 следует f (x1)
х2 следует f (x1)  f (x2) для всех x1, x2
f (x2) для всех x1, x2  А.
А.
Функцию f: X  Y называют n-местной функцией над множеством А, если Y = A и X = An.
Y называют n-местной функцией над множеством А, если Y = A и X = An.
|
|
|
Предикатом называют функцию, областью значений которой является множество символов-цифр {0, 1}. При этом говорят, что предикат P: X  {0, 1} истинен для x
{0, 1} истинен для x  X, если P (x) = 1, и ложен, если P (x) = 0. Отношение на множестве Х – это двухместный предикат P: X2
X, если P (x) = 1, и ложен, если P (x) = 0. Отношение на множестве Х – это двухместный предикат P: X2  {0, 1}.
{0, 1}.
Алфавитом называют непустое конечное множество символов. Например, V1 = { a, b }, V2 = {0, 1}, V3 = { a, +, 1, =} – алфавиты. Словом в алфавите V называется конечный объект, получаемый выписыванием одного за другим символов V, например, а + 1 = 1 + а – слово в алфавите V3, 101011 – слово в алфавите V2, abaab – слово в алфавите V1. Длина слова – число символов в нем, пустое слово не содержит ни одного символа.
Множество всех слов в алфавите V обозначается V*.
n-местной словарной функцией над алфавитом V называют n -местную функцию над V*, т. е. функцию из V*  V*
V*  …
…  V* (n раз) в V*.
V* (n раз) в V*.
Понятие графа
Направленным графом называется тройка G = (V, E, Ф), где V - множество вершин, Е – множество дуг, а Ф – функция из Е в (V  {w})2, w
{w})2, w  V. Дуга е называется входом графа, если Ф(е) = (w, u), для u
V. Дуга е называется входом графа, если Ф(е) = (w, u), для u  V
V  {w}; внутренней, если Ф(е) = (u1, u2) для u1,u2
{w}; внутренней, если Ф(е) = (u1, u2) для u1,u2  V; выходом, если Ф(е) = (u,w), для u
V; выходом, если Ф(е) = (u,w), для u  V
V  {w}. Дуга е, являющаяся одновременно и входом и выходом графа, называется висячей; для нее Ф(е) = (w,w). Дуги, не являющиеся внутренними, называются также свободными.
{w}. Дуга е, являющаяся одновременно и входом и выходом графа, называется висячей; для нее Ф(е) = (w,w). Дуги, не являющиеся внутренними, называются также свободными.
|
|
|
 Говорят, что дуга е инцидентна вершине u, если е выходит из u или ведет в u. Две дуги смежны, если существует хотя бы одна инцидентная им обеим вершина. Вершина u называется наследником вершины u', если в графе имеется хотя бы одна такая дуга, что Ф(е) = (u', u).
Говорят, что дуга е инцидентна вершине u, если е выходит из u или ведет в u. Две дуги смежны, если существует хотя бы одна инцидентная им обеим вершина. Вершина u называется наследником вершины u', если в графе имеется хотя бы одна такая дуга, что Ф(е) = (u', u).
Изображенный на рисунке 1.1. граф G1 содержит 4 вершины, 8 дуг. Дуга е1 – входная, дуга е6 – выходная, дуга е8 – висячая, остальные дуги внутренние; вершины u1 и u3 наследники вершины u1.
Путем в графе G называется последовательность …u iei u i+1 … дуг и вершин, такая, что для всех i Ф(еi) = (u i,u i+1). Образом пути называется слово, составленное из пометок проходимых дуг и вершин.
Две вершины u1,u2 графа G называются связанными, если u1 = u2 или существует маршрут е1, …, еn графа G такой, что дуга е1 инцидентна вершине u1, а дуга еn – вершине u2.
Дата добавления: 2015-12-20; просмотров: 19; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
