Случай разных корней, среди которых есть комплексные сопряженные
; 
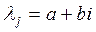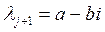тогда 
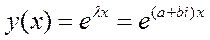
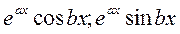-функции, входящие в Ф.С.Р.
Сопряженный корень не порождает новых вещественных линейно независимых решений.
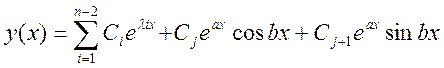-общее решение
3. Случай кратных действительных корней.
Пусть λ1 – корень кратности k.
Свойство: p(λ1)=p’(λ1)=…=p(k-1)(λ1)=0; pk(λ1)≠0.
Продифференцируем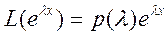 
n раз по λ: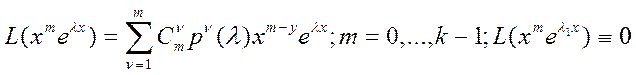 
Ф.С.Р.: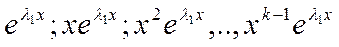 
6. Как решить задачу Коши при помощи формулы общего решения?
Пусть дано однородное линейное Д.У.:
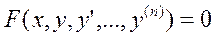Пусть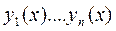 
- Ф.С.Р.=>
y(x) =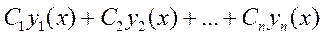 
(1) - общее решение линейного однородного уравнения в области: a<x<b; |y|<∞;…;|y(n-1)|< ∞.
Для решения задачи Коши, введем начальные условия: х0, у(х0), y’(x0), …, у(n-1)(x0)
Дифференцируем общее решение (1) n-1 раз:
y(x) =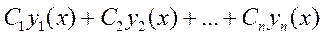
y’(x) =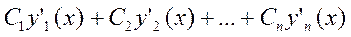 
……………………………………………………….
y(n-1)(x) =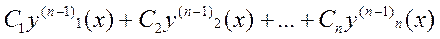 
приравниваем, соответственно к начальным условиям, разрешаем систему, относительно С – подставляем в общее решение - получаем решение задачи Коши.
7. Как найти общее решение неоднородного линейного уравнения, если известно одно частное решение этого уравнения и общее решение соответствующего однородного уравнения?
Рассмотрим 
(1)
y1(x)-решение уравнения (1) => L(y1(x))≡f(x); y(x)=y1(x)+z(x). Для каких z(x), y(x) – решение (1)?
L(y1(x),z(x))=L(y1(x))+L(z(x))≡f(x). L(z(x))=0: z(x)=C1z1+C2z2+…+Сnzn.
y(x)= y1(x)+ C1z1+C2z2+…+Сnzn.
L(y(x))=f1(x)+f2(x);
y1(x): L(y1(x))≡f1(x)
y2(x): L(y2(x))≡f1(x)
y1(x)-частное решение неоднородного уравнения, z(x)-общее решение соответствующего однородного уравнения
8. В чём состоит метод Лагранжа, используемый для нахождения общего решения неоднородного уравнения?
|
|
|
(1)
;
+
;
+
;
……………………………………………………………….
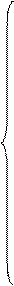
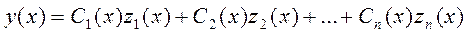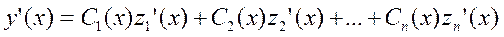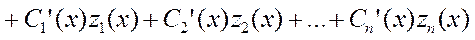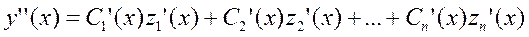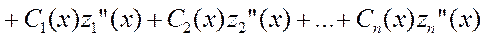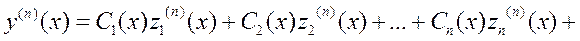
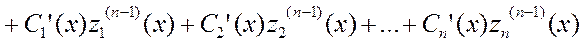
(при составлении данной системы, учитывали, что части с 
(х)=0)
Подставим все в уравнение (1):
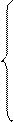
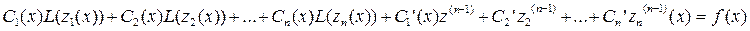Составляем систему по принципу: у(х)=0, y’(x)=0…y(n-1)=f(x):
……………………………………………………………..
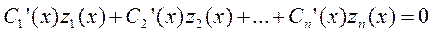
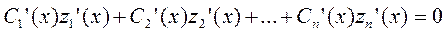
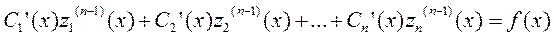
W системы ≠0=> система имеет 1 решение по отношению к Сi’(x)
Сi’(x)=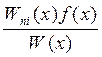 
=> Сi(x)= 
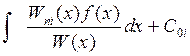; i=1..n
y(x)=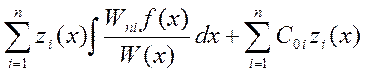 
-общее решение неоднородного уравнения
9. В каких случаях и в каком виде может быть записано частное решение неоднородного линейного уравнения с постоянными коэффициентами при использовании метода неопределённых коэффициентов?
Метод неопределенных коэффициентов применяется для некоторых видов правых частей:
1) p(x)*eαx
2) p(x)*(cos x или sin x)eαx
1.
f(x)=Pm(x)* eαx;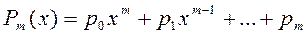 
; m≥0; α-веществ. или комплексн.
А) Случай – α-не корень характеристического уравнения: P(α)≠0
Частное решение: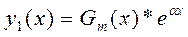 
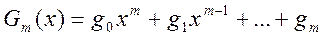; gi-неизвестные коэффициенты. Приводим подобные (при одинаковых степенях приравниваем), находим gi
В) Случай - α-корень характеристического уравнения кратности k:
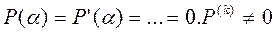
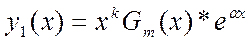
2.
C) Случай – f(x)=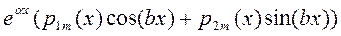 
где p1, p2 – известные полиномы от х, хотя бы 1 из них = m (размерность)
Пусть α+bi≠комплексным корням характеристического полинома, α, b- параметры функции правой части
|
|
|
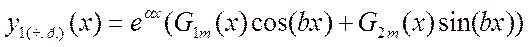
D) Случай α+bi -комплексные корни характеристического полинома, кратности k.
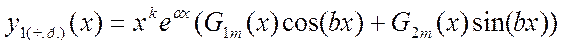
10. Как строится фундаментальная система решений в зависимости от вида характеристических чисел (действительные разные).
Эйлер предложил записывать Ф.С.Р. в виде у=eλix
Подставим в уравнение: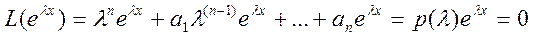 
p(λ)=0 – характеристический полином, имеющий n корней λi-характеристические числа
1. Случай действительных различных корней диф. ур-я:
; 
;…; 
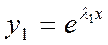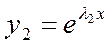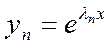- Ф.С.Р.
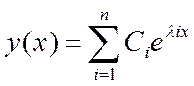-общее решение однородного уравнения
11. Как строится фундаментальная система решений в зависимости от вида характеристических чисел (комплексные сопряжённые).
Дата добавления: 2015-12-18; просмотров: 14; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!