Навчання нейронних мереж

⇐ ПредыдущаяСтр 4 из 9Следующая ⇒

Процес функціонування НМ, тобто ті дії, які вона здатна виконувати, залежить від величин синаптичнких зв'язків, тому, задавшись певною структурою штучної НМ, що відповідає якій-небудь задачі, розроблювач мережі повинен знайти оптимальні значення всіх змінних вагових коефіцієнтів (деякі синаптичні зв'язки можуть бути постійними). Цей етап називається навчанням штучної НМ (рис. 6.5), і від того, наскільки якісно він буде виконаний, залежить здатність мережі розв’язувати поставлені перед нею проблеми під час функціонування.

Алгоритм навчання являє собою набір формул, що дозволяє за вектором помилки обчислити необхідні поправки для ваг мережі. Після багаторазового подання прикладів ваги мережі стабілізуються, причому мережа дає правильні відповіді на всі (або майже всі) приклади з бази даних. У програмних реалізаціях можна бачити, що в процесі навчання функція помилки (наприклад, сума квадратів помилок по всіх виходах) поступово зменшується. Коли функція помилки досягає нуля або прийнятного малого рівня, тренування зупиняють, а отриману мережу вважають натренованою й готовою до застосування на нових даних.

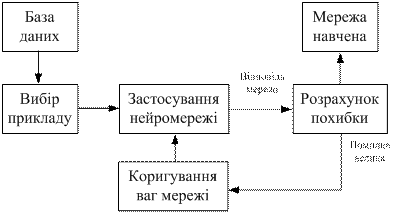
Рисунок 6.5 - Схема процесу навчання нейромережі

У процесі функціонування НМ формує вихідний сигнал Y відповідно до вхідного сигналу X, реалізуючи деяку функцію Y=G(X). Якщо архітектура мережі задана, то вид функції G визначається значеннями синаптичних ваг і зсувів мережі.

Нехай розв’язком деякої задачі є функція Y=F(X), що задана парами вхідних-вихідних даних (X¹, Y¹), (X², Y²),..., (X^N, Y^N), для яких Y^k= F(X^k) (k = 1, 2,..., N).

Навчання полягає в пошуку (синтезі) функції G, наближенної до F з деякою функцією помилки Е (рис. 6.5).

Якщо вибрано безліч навчальних прикладів - пар (X^k, Y^k), де k = 1, 2,..., N і спосіб обчислення функції помилки Е, то навчання НМ перетворюється на задачу багатовимірної оптимізації, що має дуже велику розмірність. При цьому, оскільки функція Е може мати довільний вигляд, навчання в загальному випадку - це багатоекстремальна задача оптимізації, для розв’язку якої можуть бути використані наступні (ітераційні) алгоритми:

- алгоритми локальної оптимізації з обчисленням частинних похідних першого порядку – ґрадієнтний алгоритм (метод найскорішого спуску), методи з одновимірною й двовимірною оптимізацією цільової функції в напрямку антиґрадієнта і т.ін.;

- алгоритми локальної оптимізації з обчисленням частинних похідних першого й другого порядку (метод Ньютона, Ґаусса-Ньютона, Левенберга-Марквардта й ін.);

- стохастичні алгоритми оптимізації - пошук у випадковому напрямку, метод Монте-Карло (числовий метод статистичних випробувань);

- алгоритми глобальної оптимізації.

Розглянемо ідею одного з найпоширеніших алгоритмів навчання - алгоритму зворотного поширення помилки (back propagation). Це ітеративний ґрадієнтний алгоритм навчання, який використовують з метою мінімізації середньоквадратичного відхилення поточного виходу від бажаного виходу в багатошарових НМ.

Алгоритм зворотного поширення використовують для навчання багатошарових НМ з послідовними зв'язками (рис. 6.4, б). Як зазначено вище, нейрони в таких мережах поділяються на групи із загальним вхідним сигналом - шари, при цьому на кожний нейрон першого шару подаються всі елементи зовнішнього вхідного сигналу, а всі виходи нейронів q-гo шару подаються на кожний нейрон шару (q+1). Нейрони виконують зважене (з синаптичними вагами) підсумовування елементів вхідних сигналів; до даної суми додається зсув нейрона. Над отриманим результатом потім виконується нелінійне перетворення за допомогою активаційної функції. Значення функції активації є виходом нейрона.

У багатошарових мережах оптимальні вихідні значення нейронів усіх шарів, крім останнього, як правило, невідомі, й мережу з трьома й більше шарами вже неможливо навчити, керуючись тільки величинами помилок на виходах НМ. Найбільш прийнятним варіантом навчання в таких умовах виявився ґрадієнтний метод пошуку мінімуму функції помилки з розглядом сигналів помилки від виходів НМ до її входів, тобто в напрямку,
зворотному прямому поширенню сигналів у звичайному режимі
роботи. Цей алгоритм навчання НМ одержав назву процедури
зворотного поширення.

У даному алгоритмі функція помилки являє собою суму квадратів помилки бажаного й реального виходу мережі. При обчисленні елементів вектора ґрадієнта використаний своєрідний вид похідних функцій активації сигмоїдального типу. Алгоритм діє циклічно (ітеративно), і його цикли називають епохами. На кожній епосі на вхід мережі по черзі подаються всі навчальні спостереження, вихідні значення мережі порівнюються з цільовими значеннями й обчислюється помилка. Значення помилки, а також ґрадієнта поверхні помилок використовуються для коригування ваги, після чого всі дії повторюються. Початкова конфіґурація мережі вибирається випадковим чином, і процес навчання припиняється або коли пройдена певна кількість епох, або коли помилка досягне деякого певного рівня малості, або коли помилка перестане зменшуватися (користувач може сам вибрати потрібну умову зупинки).

Нижче наведений покроковий словесний опис алгоритму зворотного поширення.

1. Вагам мережі присвоюються невеликі початкові значення.

2. Вибирається чергова навчальна пара (X,Y) з навчальної множини; вектор X подається на вхід мережі.

3. Обчислюється вихід мережі.

4. Обчислюється різниця між необхідним (цільовим, Y) і реальним (обчисленим) виходом мережі.

5. Ваги мережі коригують так, щоб мінімізувати помилку (спочатку ваги вихідного шару, потім, з використанням правила диференціювання складної функції й зазначеного своєрідного виду похідній сигмоїдальної функції - ваги попереднього шару й т.ін.).

6. Кроки з 2-го по 5-й повторюються для кожної пари навчальної множини доти, доки помилка на всій множині не досягне прийнятної величини.

Пункти 2 і 3 подібні до тих, які виконуються у вже навченій мережі. Обчислення в мережі виконуються пошарово. На 3-му кроці кожний з виходів мережі віднімається від відповідного компонента цільового вектора з метою одержання помилки. Ця помилка використовується на 5-му кроці для корекції ваг мережі. Пункти 2 і 3 можна розглядати як «прохід уперед», тому що сигнал поширюється по мережі від входу до виходу, а 4 і 5 становлять «зворотний прохід», оскільки сигнал помилки поширюється назад по мережі й використається для підстроювання ваг.

Класичний метод зворотного поширення відносять до алгоритмів з лінійною збіжністю. Його відомими недоліками є: невисока швидкість збіжності (велика кількість ітерацій, необхідних для досягнення мінімуму функції помилки), можливість сходитися не до глобального, а до локальних розв’язків (локальних мінімумів зазначеної функції). Можливий також “параліч“ мережі, при якому більшість нейронів функціонують при значно більших значеннях арґументу функції активації, тобто на її пологій ділянці (оскільки помилка пропорційна похідній, що на даних ділянках мала, то процес навчання практично завмирає).

Для усунення цих недоліків були запропоновані численні модифікації алгоритму зворотного поширення, які пов'язані з використанням різних функцій помилки, різних процедур визначення напрямку й величини кроку й под.

Розглянутий алгоритм навчання НМ за допомогою процедури зворотного поширення передбачає наявність якоїсь зовнішньої ланки, що надає мережі, крім вхідних, також і цільові вихідні образи. Алгоритми, що користуються подібною концепцією, називаються алгоритмами навчання “з учителем”. Для їх успішного функціонування необхідна наявність експертів, що створюють на попередньому етапі для кожного вхідного образа еталонний вихідний.

Процес навчання “без вчителя”, як і у випадку навчання “з учителем”, полягає в підстроюванні ваг синапсів. Очевидно, що підстроювання ваг синапсів може проводитися тільки на підставі інформації, доступної в нейроні, тобто інформації про його стан, уже наявних вагових коефіцієнтів і поданого вхідного вектора X. Виходячи з цього, за аналогією з відомими принципами самоорганізації нервових клітин побудовані алгоритми навчання Хеба й Кохонена. Загальна ідея даних алгоритмів полягає в тому, що в процесі самонавчання шляхом відповідної корекції вагових коефіцієнтів підсилюються зв'язки між збудженими нейронами. Головна риса, що робить навчання без вчителя привабливим - це його «самостійність». Слід зазначити, що вид відгуків Y на кожний клас вхідних образів невідомий заздалегідь і буде являти собою довільне сполучення станів нейронів вихідного шару, зумовлене випадковим розподілом ваг на стадії ініціалізації. Разом з тим, мережа здатна узагальнювати схожі образи, відносячи їх до одного класу. Тестування навченої мережі дозволяє визначити топологію класів у вихідному шарі.

Серед різних конфігурацій штучних НМ зустрічаються такі, при класифікації яких за принципом навчання, не підходять ні навчання із учителем, ні навчання без учителя. У таких мережах вагові коефіцієнти синапсів розраховуються тільки один раз перед початком функціонування мережі на основі інформації про оброблювані дані, й усе навчання мережі зводиться саме до цього розрахунку. З одного боку, надання апріорної інформації можна розцінювати, як допомогу вчителя, але з іншого боку - мережа фактично просто запам'ятовує зразки до того, як на її вхід надходять реальні дані, й не може змінювати свою поведінку, тому говорити про ланку зворотного зв'язку з учителем не доводиться. Зпоміж мереж із подібною логікою роботи найбільш відомі мережа Хопфілда й мережа Хемінга, які звичайно використовують для організації асоціативної пам'яті.

Персептрони

Прагнучи відтворити функції людського мозку, дослідники створили прості апаратні (а пізніше програмні) моделі біологічного нейрона й системи його з'єднань. Перше систематичне вивчення штучних НМ було започатковане Макалохом і Пітсом 1943 р. Пізніше вони досліджували мережні парадигми для розпізнавання зображень, що піддають зрушенням і поворотам, використовуючи при цьому просту нейронну модель, показану на рис. 6.6. Елемент S множить кожний вхід х_i на вагу w_i і підсумовує зважені входи. Якщо ця сума більша за задане граничне значення, вихід дорівнює одиниці, у протилежному випадку - нулю. Ці системи (і безліч подібних до них) одержали назву персептронів. Вони складаються з одного шару штучних нейронів, з'єднаних за допомогою вагових коефіцієнтів з безліччю входів.

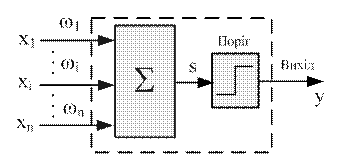
Рисунок 6.6 - Персептронний нейрон

Розглянемо як приклад тринейронний персептрон (рис. 6.7), нейрони якого мають активаційну функцію у вигляді одиничного стрибка.

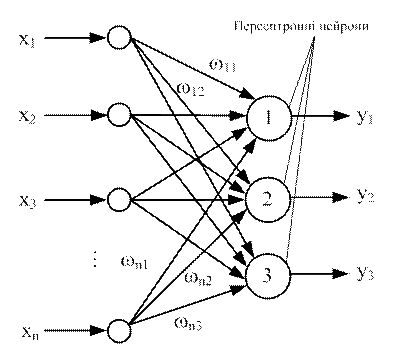
Рисунок 6.7 - Персептрон з багатьма виходами

На n входів надходять вхідні сигнали, що проходять по синапсам на три нейрони, які утворюють єдиний шар цієї мережі й видають три вихідні сигнали:

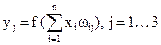Усі вагові коефіцієнти синапсів одного шару нейронів можна звести в матрицю W, у якій кожний елемент 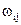задає величину i-го синаптичного зв'язку j-гo нейрона. Таким чином, процес, що відбувається в НМ, може бути записаний у матричній формі:

Y=f(XW),

де X і Y - відповідно вхідний й вихідний сигнальні вектори-рядки; f(S) - активаційна функція, що застосовується для кожного елемента вектора S.

На рис. 6.8 зображений двошаровий персептрон, отриманий з персептрона, зображеного на рис. 6.7, шляхом додавання другого шару, що складається з двох нейронів.

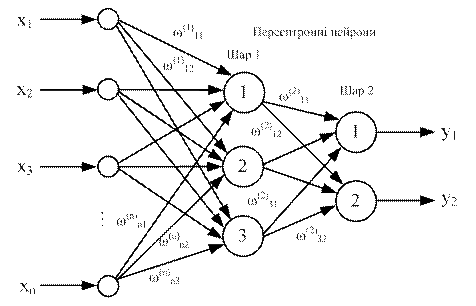
Рисунок 6.8 - Двошаровий персептрон

Фактично така Q-шарова НМ еквівалентна мережі з одним прихованим шаром з ваговою матрицею єдиного шару :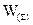

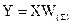Робота персептрона зводиться до класифікації (узагальнення) вхідних сигналів, що належать n-вимірному простору за деяким числом класів. З математичної точки зору це відбувається шляхом розбиття простору площинами. Для випадку одношарового персептрона:

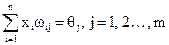Кожна отримана область є областю визначення окремого класу. Число таких класів для персептрона не перевищує 2ⁿ, де n- число його входів. Однак не всі з класів можуть бути виділені даною НМ (проблема виключного «АБО»).

Навчання персептрона зводиться до формування ваг зв'язків між першим й другим шарами відповідно до наступного алгоритму:

- ініціалізація елементів вагової матриці (зазвичай невеликими випадковими значеннями);

- подання на входи одного з вхідних векторів, які мережа повинна навчитися розрізняти й обчислити його вихід;

- якщо вихід правильний, продовжити навчання НМ, інакше – обчислити різницю між ідеальним d і отриманим Y значеннями виходу d=d–Y, модифікувати ваги 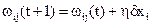, де t, (t+1) - номери поточної й наступної ітерацій відповідно; h - коефіцієнт швидкості навчання (0 <h< 1); i - номер входу; j - номер нейрона в шарі; при d>Y вагові коефіцієнти збільшуються, зменшуючи помилку, у протилежному випадку – зменшуються.

- повернутися до навчання НМ пред'являючи на різних ітераціях по черзі у випадковому порядку всі можливі вхідні вектори, доки мережа не перестане помилятися.

Дата добавления: 2015-12-18; просмотров: 27; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 Следующая ⇒

Мы поможем в написании ваших работ!