Упругие свойства листов кожкартона
Автором были проведены опыты с образцами кожкартона на установке «INSTRON» (Великобритания), позволяющей воспроизводить диаграммы, выражающие зависимость между усилиями, прикладываемыми к образцам, и деформациями этих образцов при разных скоростях нагружения и релаксации. В результате действий согласно рабочей инструкции установки «INSTRON», были получены диаграммы растяжения и сжатия образцов кожкартона марки 3-1-11 двух типов: типа А с повышенным содержанием кожи до 70% и типа В с содержанием кожи около 25%. Диаграммы изображены на рис. 3.2 – 3.5.
На рис. 3.2 изображены диаграммы растяжения до разрушения полосы кожкартона типа А толщиной h = 1,73 мм и шириной 25 мм с базой 50 мм. Скорость нагружения 50 мм/мин. Растяжение производилось вдоль волокон, т.е. вдоль оси 
(диаграммы 1А) и поперек волокон - вдоль оси 
(диаграммы 2А). При этом для увлажненных до вырубочной кондиции (30% влаги) полос (диаграммы, помеченные символами Вл) разрывное напряжение оказалось больше, чем для сухих полос (диаграммы с символами С). Видно, что разрывное усилие и предел приближенной пропорциональности напряжения σ и относительной деформации ε для полос типа А в направлении больше, чем в направлении . То же характерно и для полос типа В, диаграммы растяжения которых приведены на рис. 3.3. Но для влажных полос типа В разрывное усилие меньше, чем для сухих.
Рис. 1.3
Графики отражают два характерных участка деформации: участок 
, условно называемый участком упругости (превалирующая часть деформации - упругая), и участок 
- участок пластичности. Предельное напряжение, при котором деформация считается упругой, будем называть пределом упругости (
). Для материала типа А эта величина примерно равна 
. Для материала типа В 
|
|
|
На рис. 3.4 представлены релаксационные характеристики образцов кожкартона типов А и В Б полученные в результате быстрого растяжения их до предела упругости с последующей медленной релаксацией. Скорость релаксации 
Из вида этих диаграмм следует, что деформации растяжения листов характеризуются вязкостью и ползучестью.
На рис. 3.5 изображены диаграммы сжатия и последующей релаксации пачки из 15 слоев (листов) влажных образцов типов А и В. Для этих диаграмм характерна положительность второй производной 
, а также наличие протяженного участка малой крутизны. Наличие этого участка можно объяснить пластической деформацией набухших поверхностных слоев, сопровождающейся перераспределением влаги между волокнами, и распрямлением первоначально прогнутых участков пластин. Пологий участок каждой диаграммы характеризуется в основном цилиндрической жесткостью разгибания листов, а крутой (после сжатия до величины деформации ε порядка 1,0 – 1,2) – жесткостью пачки как сплошного массива спецкартона.
|
|
|
Диаграммы выражают анизотропию упруго – пластических свойств и нелинейную зависимость между напряжением и деформацией.
Условно линейными можно считать упругие характеристики растяжения – сжатия в направлениях и до величины ε = 0,005; при этом условные модули упругости равны (соответственно в направлениям и ) 
= 1200 МПа и 
= 600 МПа для листов кожкартона типа А; = 1000 МПа и = 400 МПа для листов типа В. При сжатии в направлении оси 
(вдоль нормали к поверхности листа) предлагается принять в качестве оценочных значения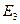 
= 500 МПа для материала типа А и 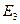= 300 МПа для материала типа В.
Рис. 3.4
Для оценки упругих параметров, характеризующих сдвиг в плоскостях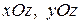 
, были собраны специальные стенды (рис. 3.6). На рис. 3.6 (а) изображен стенд для кручения образцов типов А и В в плоскости 
вокруг оси . Образцы имели вид полосок длиной 
, прямоугольного сечения (толщина 
и ширина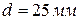 
). Полученные диаграммы зависимости крутящего момента М от угла поворота 
крайнего сечения изображены на рис. 3.7.
Рис. 3.5
Величина, условно принимаемая здесь как модуль сдвига 
, рассчитанная для некоторого участка 
, находится по формуле [32]:
|
|
|
,
где 
- средняя точка промежутка ;
.
Для участка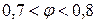 
, например, получается 
=1000 МПа для материала типа А.
На рис. 3.6, б изображена схема стенда для исследования крутильных колебаний обруча массой 
и радиусом 
. Обруч подвешивался на полоске кожкартона длиной 
и того же сечения, что и в пре-
Рис. 3.6
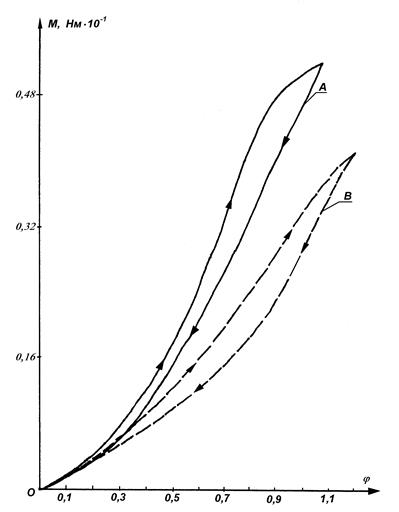
Рис. 3.7
дыдущем опыте. С помощью определения периода Т малых крутильных колебаний была рассчитана та же величина для участка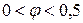 
:
,
где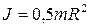 
- момент инерции обруча относительно оси вращения .
Здесь 
.
Для определения прижимного усилия, действующего со стороны сдвигающего валика на верхний лист пачки кожкартона, нужно достаточно строго отслеживать соотношение между этим усилием и деформацией сжатия пачки. Предложим следующую трактовку результатов опытов по сжиманию пачки образцов.
Нагрузочные части диаграмм рис.3.5 демонстрируют разгибание образцов картона. Как отмечалось выше, листы обычно имеют вид цилиндрических пластин, сечение которых близко к синусоиде. Образцы, составлявшие пачку, имели форму квадратов со стороной 50 мм, так что их сечения представляли собой малые фрагменты синусоиды.
|
|
|
Считая сжимаемые образцы цилиндрическими оболочками, оценим их изгибную жесткость. Пусть нейтральная ось сечения есть отрезок кривой, заключенный в прямоугольник шириной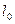 
и высотой H+βh, где h – толщина листа, β < 1 – коэффициент, определяющий положение нейтральной оси (рис. 3.8). Эта ось для криволинейного стержня или оболочки смещена относительно центра тяжести сечения. Величины h и Н малы по сравнению с шириной прямоугольника.
Рассмотрим баланс энергии при сжатии оболочки вертикальной силой. Будем считать параллелепипед размерами 
, в который заключена оболочка, упругим телом, имеющим модуль упругости 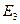при вертикальном сжатии.
Тогда потенциальная энергия сжатого на величину 
параллелепипеда равна примерно
где 
- относительная деформация высоты параллелепипеда, 
- его объем.
Пренебрегая эффектом стеснения поперечной деформации при изгибе пластинки [24], составим выражение для ее потенциальной энергии:
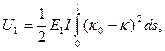
где - среднее значение модуля упругости материала оболочки при его сжатии и растяжении в направлении оси (или ); I - момент инерции сечения листа, 
- изменение кривизны изогнутой нейтральной оси сечения в результате деформации; l – длина этой оси; ds - дифференциал длины дуги этой кривой.
Обозначим: 
Приравняв 
и считая, что момент инерции I c точностью до малых второго порядка включительно равен центральному моменту и равен 
, получим:
Рис.1.8
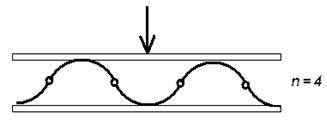
Рис.1.9
Рис. 1.10
Рассмотрим случай, когда дуга нейтральной оси является выпуклой кривой, кривизна κ которой нигде не равна нулю. Тогда она мало отличается от сегмента окружности, вписанного в прямоугольник. Длина l дуги этого сегмента с принятой точностью (до малых второго порядка включительно) равна .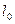
Кривизна дуги равна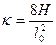 
.
Тогда
, (1.2)
и из формулы (3.1) получаем:
. (1.3)
Здесь обозначено: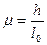 
.
Для образца вида А с параметрами h = 2мм =H, 
и 
получим 
, что несколько меньше средних значений, соответствующих пологой части графика на рис.3.5. Реальная жесткость больше из-за присутствия образцов, искривленных более сложным образом. Для модели, изображенной на рис.3.9, формула (3.3) трансформируется в формулу
,
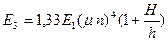где n – количество сегментов.
Для рассчитанного выше значения 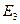величина n оказывается дробной (порядка 1.65) и означает осредненное количество дуг сегментов в пачке образцов.
Дадим оценку сверху для величины 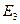в случае, когда нейтральная ось сечения имеет вид одной целой волны синусоиды (рис.3.10).
Пусть нейтральная ось (синусоида), до деформации описывавшаяся уравнением
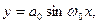
деформируется в синусоиду же вида
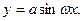
Здесь, с учетом принятой точности,
, 
Величину ω можно рассчитать, если пренебречь растяжением нейтральной оси и приравнять длину волны синусоиды после деформации к длине до деформации.
Длина эта равна:
где k = aω,
- эллиптический интеграл второго рода [33].
Поскольку Н мало по сравнению с l, то и параметр k мал, и тогда в разложении эллиптического интеграла в ряд [33], можно оставить только члены порядка до 
включительно:
Следовательно, 
и из равенства 
находим величину ω.
Найдем кривизну синусоиды в ее вершине:
В результате для величины 
, которая входит в выражение интеграла J в формуле (3.1) имеем оценку:
Если предположить, что для весьма пологой синусоиды величина меняется вдоль кривой почти линейно от нуля до найденного максимального значения, то ее среднее значение втрое больше, чем в выражении (3.2) для кругового сегмента.
Дата добавления: 2015-12-17; просмотров: 21; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!