Конвейер команд. Временные проблемы конвейера (временные диаграммы).

Конвейер - устройство, реализующее такой метод обработки команд внутри микропроцессора, при котором исполнение команды разбивается на несколько этапов. На стадии выполнения каждая машинная команда разбивается на более элементарные операции. Для выполнения каждого этапа операции имеется от­дельный аппаратный блок. Эти блоки соединены в линию так, чтобы результат выполнения в данном блоке некоторого этапа передавался для реализации оче­редного этапа на следующий блок, все блоки функционируют одновременно.

Если для выполнения любого этапа операции выделено одно и тоже время t_T (такт конвейера), то такой конвейер называется синхронным.

Рассмотрим рабочий цикл процессора (Пр). Выполнение любой команды Пр складывается из нескольких различных этапов, каждый из которых выполня­ется своим функциональным узлом.

Рассмотрим пример: выполнение одноадресной машинной арифметической операции без использования конвейерной обработки. Этапы рабочего цикла:

- этап 1 - формирование адреса команды – t₁

- этап 2 - чтение команды из оперативной памяти (ОП) –t₂

- этап 3 -формирование адреса операнда – t₃

- этап 4 - чтение операнда из памяти – t₄

- этап 5 - выполнение арифметической операции – t₅

Если длительность i-ого этапа равна t_i и все этапы выполняются последова­тельно, то

t_посл. =t_l+t₂+t₃+t₄+t₅ (1.1)

Временная диаграмма работы одноадресной машины при последовательном вы­полнении команд представлена на рис. 1.1.

Принято, что t_l=t₃<t₂=t₄<t₅=t_T

Производительность определяется по формуле:

(1.2)

При рассмотрении функционирования конвейера основная задача состоит в определении такта. Далее поступим следующим образом:

1) Определяем такт конвейера. Обозначим через t_T (время такта) величину t_T=max{t_i}

и будем требовать, чтобы для любых i=1,2,3,..., выполнялось условие t_i+t_i+1>t_T

Иначе говоря, в качестве времени такта t_T выберем длительность наиболее продолжительного этапа операции, а саму разбивку на этапы производим та­ким образом, чтобы никакие два последовательных этапа не могли быть вы­полнены за время одного такта.

2) Другой способ, которым можно действовать в этом случае, состоит в том, что­бы разделить на части наиболее длительный этап и таким образом уменьшить время такта.

Например, может оказаться, что самым длительным этапом является работа арифметического устройства, когда оно выполняет операцию умножения. Если это так, то множительное устройство можно построить в виде двух самостоя­тельных функциональных узлов, каждый со своими входными и выходными регистрами, из которых первый выполнял бы умножение множимого на млад­шие разряды множителя, а второй - умножение множимого на старшие разря­ды множителя и сложение с результатом, полученным первым функциональ­ным узлом.

Когда условия t_i<t_T t_i+t_i+1>t_T (i=1,2,3,…n) (1.4)

так или иначе, удовлетворены. Функциональные узлы, выполняющие последо­вательные этапы операции, целесообразно выстроить в единую конвейерную линию, в которой устройство, выполняющее этап 1, закончив его для одной операции, переходило бы в следующем такте к выполнению своего этапа для следующей операции и т.д.

Быстродействие в синхронном конвейере (номинальное) равно:

Количество этапов, на которые разделено выполнение каждой операции, на­зывается глубиной перекрытия, т.е. определяет количество ступеней конвейера. В каждом такте на конвейере находится одновременно п последовательных опера­ций. Чем больше глубина перекрытия, тем больший выигрыш в быстродействии может быть получен.

Из условия t_i < t_T, i = 1,2,...,n следует:

t_посл = , (1.6)

а из условий t_i+t_i+1>t_T следует (1.7)

или

Таким образом,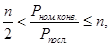

т.е. выигрыш в номинальном быстродействии получается в

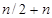раз.

Отношение представляет собой предельный выигрыш в быстродействии при синхронном конвейере с глубиной перекрытия n.

Реальный выигрыш по быстродействию оказывается всегда меньше пре­дельного выигрыша. Это объясняется двумя факторами:

1) некоторые операции могут выполняться за меньшее количество тактов, чем обычные арифметические операции, в виду чего отдельные функциональные узлы, включенные в конвейер, при выполнении данных операций простаивают.

2) при выполнении некоторых операций на определенных этапах могут потребоваться результаты более поздних этапов предыдущих операций, либо при вы­полнении некоторых операций результаты определенных этапов могут влиять на более ранние этапы следующих, ввиду чего приходится приостанавливать конвейер. Этот фактор проявляется при выполнении операций условного пере­хода.

Пример выполнения операции условного перехода по результату арифметической oпeрации. Если бы временная диаграмма строилась по последовательному принципу, то такая операция выполнилась бы всего в 2 такта: формирование адреса, команда условного перехода и чтение команды условного перехода из ОП, после чего не­обходимо переходить к формированию адреса следующей команды. Однако при конвейерной организации условный переход оказывается длиннее обычных операций.

Рассмотрим пример влияния на производительность конвейера команды ус­ловного перехода по результату арифметической операции при конвейерной обработке команд (Рис. 1.3). Временная диаграмма работы конвейера для сле­дующих операций:

Показан случаи, когда условие перехода выполняется, т.е. прихо­дится заново формировать адрес следующей команды. Заштрихованы те такты, когда не используются отдельные устройства, включенные в конвейер. При вы­полнении операции (2) пересылка данных в регистр - в шестом такте простаивает АЛУ, а при выполнении (3) операции - УП - в пятом такте простаивает устройство формирования адреса операнда, в шестом - АЛУ. Простой конвейера равен двум тактам.

---

Дата добавления: 2015-12-17; просмотров: 66; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!