Импульс Ферми, энергия Ферми. Вычисление
СОДЕРЖАНИЕ
1 Волновые функции и энергетический спектр электрона
в потенциальном ящике 2
2 Импульс Ферми, энергия Ферми. Вычисление функции
плотности состояний и средней энергии электронного газа при Т = 0 7
Приложение А 15
Библиографический список 23
Волновые функции и энергетический спектр электрона в потенциальном ящике
Рассмотрим металл при абсолютном нуле температуры. Для решения вопроса о распределении электронов по уровням энергии и теплоемкости электронного газа используем модель, представляющую собой потенциальный ящик с бесконечно высокими стенками, внутри которого находится свободный электронный газ. Действительно, наиболее типичное, характерное свойство металлов – электропроводность, отсутствие порогового значения напряжения – подтверждает справедливость такого приближения. Кроме того, мы пренебрегаем учетом межэлектронного взаимодействия электронов проводимости с ионными остовами (модель идеального газа).
С учетом вышесказанного, задача сводится к отысканию волновых функций и энергетических уровней электрона, движущегося в потенциальной яме прямоугольной формы (для простоты расчетов) с ребрами Lx, Ly, Lz и объемом V = LxLyLz.
Уравнение Шредингера для свободного электрона:
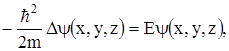
где 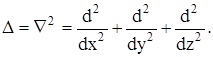
Потенциальная энергия U (x,y,z) = 0, так как газ идеальный, на границах металла имеем U®¥ при X = 0, Lx; Y = 0, Ly; Z = 0, Lz.
|
|
|
Решение ищем в виде
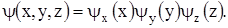
Такой вид волновой функции отражает тот факт, что направления движения электрона по координатным осям равновероятны и независимы, поэтому вероятность обнаружения электрона в области DхDуDz требует для своей реализации осуществления трех независимых событий – изменения координат x,y,z. А согласно теории вероятностей вероятность реализации нескольких независимых событий равна произведению вероятности осуществления каждого из них.
Решаем уравнение Шредингера:
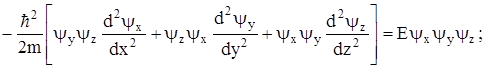
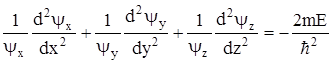 . (1)
. (1)
Так как 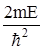 есть сугубо положительная величина, то ее можно представить в виде квадрата некоторого числа, который, в свою очередь, изображаем суммой квадратов трех независимых чисел, то есть
есть сугубо положительная величина, то ее можно представить в виде квадрата некоторого числа, который, в свою очередь, изображаем суммой квадратов трех независимых чисел, то есть
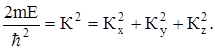
Теперь уравнение (1) может быть записано в виде, удобном для решения:
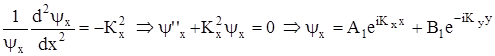 ;
;
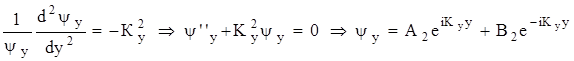 ; (2)
; (2)
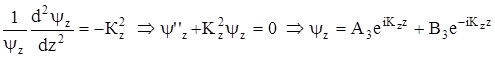 ;
;
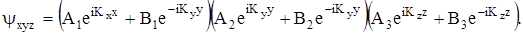
Каждое из решений (2) представляет собой плоскую волну. Действительно, используя формулу Эйлера
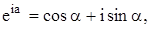
получим, например, для yх:
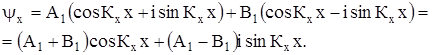
Аналогично для 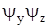 :
:
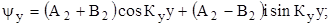
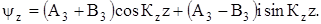
Таким образом, Кx, Кy, Кz есть не что иное, как проекции волнового вектора
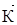 (Кx Кy Кz). Граничные условия требуют, чтобы волновая функция обращалась в нуль при х = 0, Lx; у = 0, Ly; z = 0, Lz, то есть вероятность обнаружения электрона вне параллелепипеда с ребрами Lx, Ly, Lz должна быть равна нулю.
(Кx Кy Кz). Граничные условия требуют, чтобы волновая функция обращалась в нуль при х = 0, Lx; у = 0, Ly; z = 0, Lz, то есть вероятность обнаружения электрона вне параллелепипеда с ребрами Lx, Ly, Lz должна быть равна нулю.
|
|
|
При х = 0, у = 0, z = 0 имеем
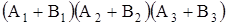 = 0,
= 0,
откуда
А1 = -В1; А2 = -В2; А3 = -В3.
При х = Lx; у = Ly; z = Lz имеем
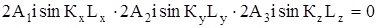 ,
,
откуда
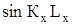 = 0;
= 0; 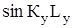 = 0;
= 0; 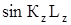 = 0.
= 0.
Таким образом:
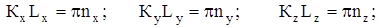
где 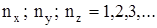
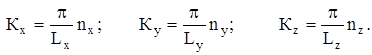 (3)
(3)
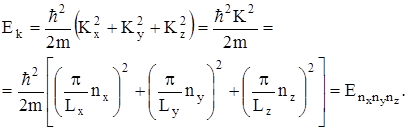 (4)
(4)
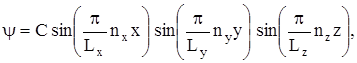 (5)
(5)
где С – постоянный коэффициент, в общем случае комплексный, определяется из условия нормировки;
nx, ny, nz – целые числа (компоненты волнового вектора) можно рассматривать как совокупность трех квантовых чисел, которые вместе со спиновым квантовым числом характеризуют собственное состояние свободного электрона. Наинизший энергетический уровень отвечает состоянию
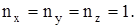
Если электрон находится в одномерном потенциальном ящике с шириной 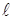 , то
, то
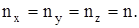
В этом случае его энергия имеет вид
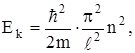 (6)
(6)
а волновая функция
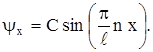 (7)
(7)
Из уравнения (6) можно, зная ширину ящика, определить номер энергетического уровня электрона, если его энергия Еn задана. Используя соотношение
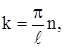 (8)
(8)
можно найти модуль волного вектора К.
Если частица находится в основном состоянии (n=1), то её энергия
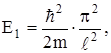 (9)
(9)
волновая функция
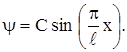
Коэффициент С можно определить из условия нормировки:
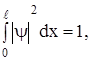
то есть вероятность обнаружения частицы в ящике равна 1 (очевидное утверждение).
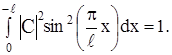
Вычислим интеграл:
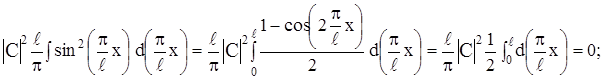
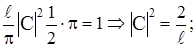
считая С действительным, имеем
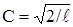 .
.
Таким образом, волновая функция свободной частицы в основном состоянии, локализованной в одномерном ящике, будет:
|
|
|
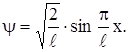 (10)
(10)
В случае возбуждения (n 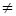 1) множитель перед синусом останется прежним, а функция примет вид
1) множитель перед синусом останется прежним, а функция примет вид
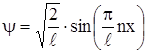 .
.
Знание вида волновой функции позволяет вычислить вероятность её обнаружения в любом заданном интервале внутри ящика. Действительно, поскольку 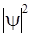 есть плотность вероятности (то есть вероятность локализации частицы внутри единичного интервала), то
есть плотность вероятности (то есть вероятность локализации частицы внутри единичного интервала), то
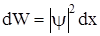 -
-
вероятность обнаружения в бесконечно малом интервале dx.
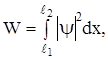 (11)
(11)
где [ 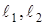 ] – интервал внутри потенциальной ямы. Естественно, [
] – интервал внутри потенциальной ямы. Естественно, [ 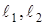 ] < [
] < [  ]
]
(в случае равенства вероятность будет равна 1).
Импульс Ферми, энергия Ферми. Вычисление
функции плотности состояний и средней энергии электронного газа при Т = 0
Для импульса электрона проводимости имеем 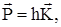 поэтому
поэтому

В соответствии с классической теорией при Т=ОК все электроны в объёме V должны были бы сконденсироваться в состояние
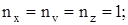
Еi ~ КТ; i = 1,2,...,
где n - номер электрона.
При Т = 0 Еi = 0. Однако это для электронов запрещено принципом Паули, в соответствии с которым в любой системе частиц С полуцелым спином данное квантовое состояние может быть занято только одной частицей. Следовательно, на каждом уровне n (nx, ny, nz) может быть только два электрона с различными спиновыми числами:
|
|
|
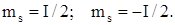
Таким образом, электроны при Т=0 будут заполнять не только два наинизших состояния:
(nx, ny, nz; ms=1/2); (nx, ny, nz; ms= - 1/2),
но столько состояний, сколько имеется электронов, пока в результате не окажется, что все уровни ниже некоторой определенной энергии Еф = Еmax заняты, а выше - свободны. Число занятых энергетических уровней будет при этом равно N/2, где N - число электронов в данном образце металла (то есть на каждом энергетическом уровне будет два электрона с противоположно ориентированными спинами). Заполненный таким образом в фазовом пространстве объём имеет вид сферы (рисунок1):
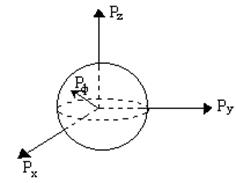
Рисунок 1
 .
.
Изоэнергетическая поверхность сферы соответствует максимальной (граничной) энергии Еф. Эта поверхность называется поверхностью Ферми, а Еф- энергия Ферми. Радиус сферы Ферми в пространстве импульсов
Рф = (2m Еmax)1/2 = (2m Eф)1/2. (12)
Найдем связь между Еф и концентрацией электронов n. Объем фазового пространства, ограниченного сферой Ферми, равен
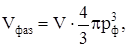
где V - геометрический объём образца металла.
Объём фазовой ячейки
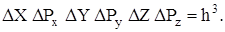
Число таких ячеек
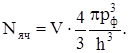
Так как в каждой ячейке может находиться по два электрона с противоположно ориентированными спинами, число электронов в фазовом пространстве
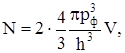
а концентрация
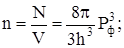 (13)
(13)
отсюда
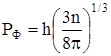 (14)
(14)
или, учитывая связь энергии и импульса (7), а также (12), может записать:
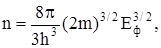 (15)
(15)
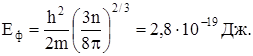 (16)
(16)
Из уравнения (16) видно, что Еф монотонно возрастает с увеличением n.Этого и следовало ожидать, поскольку электроны, добавленные к системе, содержащей n электронов, которые уже заполнили наинизшие возможные энергетические состояния, должны обязательно занять более высокие энергетические уровни, увеличивая тем самым энергию Еф - границу между заполненными и свободными состояниями.
Для объяснения того, что энергия Ферми Еф возрастает с увеличением n медленнее, чем по линейному закону, найдем функцию плотности состояний электронов для единицы объёма металла. Из (13) следует, что число состояний для электронов между бесконечно близкими изоэнергетическими поверхностями радиуса Р и Р + dP будет:
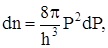
или, учитывая
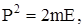
получим для числа состояний в единице объёма и приходящихся на интервал Е, Е+dE,
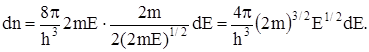 (17)
(17)
Множитель перед dE определяет функцию плотности состояний электронов для единицы объёма металла.
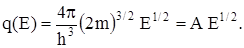 (18)
(18)
Отсюда видно, что замедление роста Еф по сравнению с линейным происходит потому, что плотность состояний q(Е) также возрастает с ростом энергии, а это означает, что при переходе к более высоким энергиям оказывается возможным разместить внутри одного и того же энергетического интервала большее число электронов.
Найдем среднюю энергию электронов при абсолютном нуле температуры. Согласно общему определению среднего значения величины имеем
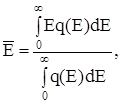
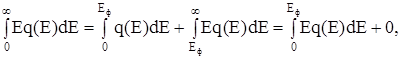
так как q(E)=0 в интервале E > Eф означает, что все электроны размещены на уровнях Е≤Eф и электронов с энергией, большей, чем фермиевская, при Т=0, просто нет. Аналогично
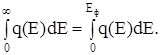
Подставляя значение
q(E) = A E1/2,
получим
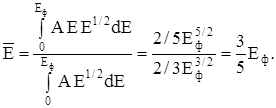 (19)
(19)
Таким образом, максимальная энергия Еф и средняя 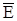 довольно близки по значению.
довольно близки по значению.
Следует обратить внимание на то обстоятельство, что средняя или максимальная энергия отдельных электронов не зависит от объёма металла при данной его плотности. Возьмём, например, два куска массой 1 и 2 кг. Второй кусок содержит в два раза больше электронов, чем первый, между тем как максимальная энергия электронов в обоих случаях одинакова, так как согласно (15) она определяется лишь концентрацией n - неизменной для одного и того же металла. Ясно, что во втором случае энергетические уровни будут в два раза гуще, чем в первом, так как в одном и том же интервале [0, Eф] придется расселить уже не N электронов, а 2N, то есть в два раза больше.
Нельзя не заметить также, что средняя кинетическая энергия электрона 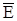 значительно больше средней тепловой энергии в классической теории. Действительно, если вычислить эффективную температуру (то есть такую температуру, которая соответствовала бы средней энергии электрона
значительно больше средней тепловой энергии в классической теории. Действительно, если вычислить эффективную температуру (то есть такую температуру, которая соответствовала бы средней энергии электрона 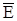 в случае его подчинения классическому распределению Максвелла-Больцмана), то мы увидим:
в случае его подчинения классическому распределению Максвелла-Больцмана), то мы увидим:
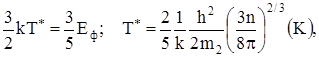
где h = 6,6∙10-34 Дж с;
m2 = 9 10-31 кг;
k = 1,38 10-23 Дж/К - постоянная Больцмана.
Вычисления дают
Т* = 8 104 К,
то есть в случае "классичности" электрона для доведения его средней энергии до того значения, которым он обладает при ОК как квантовый объект, необходимо было бы нагреть металл до температуры порядка 80000 градусов Кельвина, что само по себе исключает возможность существования металла как твердого тела.
Следовательно, большая кинетическая энергия электронов и соответствующая ей высокая средняя квадратичная скорость никак не связаны с температурой твердого тела.
Оценим величину этой скорости (19):
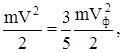 (20)
(20)
отсюда
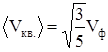 . (21)
. (21)
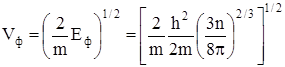 .
.
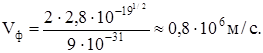
Оценим относительную долю электронов от их общего числа, участвующих в тепловом движении при комнатных температурах 300 К. Как уже упоминалось, при ОК все электроны рассеяны на N/2 энергетических уровнях по два электрона
с противоположно ориентированными спинами на каждом.
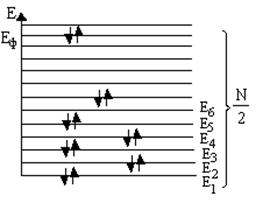
Рисунок 2
Ясно, что при повышении температуры должно начаться "переселение" электронов из нижних этажей в верхние (что соответствует росту их энергии). Но этот процесс не может затронуть "глубинные" электроны, так как их переход в верхние этажи за уровень Ферми требует сообщения им энергии, что эквивалентно, как было показано, нагреву металла на десятки тысяч градусов. Переходы же внутри интервала [Е1 Еф] невозможны, поскольку все уровни заселены парами электронов, присоединение "третьего" запрещено принципом Паули. Таким образом, доля термически активных электронов весьма невелика, приближенная оценка дает значение
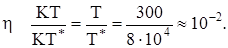
Таким образом, при комнатных температурах тепловым движением затронуты электроны, составляющие лишь доли процента от их общего числа. Приведенный расчет не учитывает зависимости функции плотности состояния от энергии:
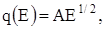
то есть предполагается, что расстояние между уровнями неизменны, тогда как на самом деле вид зависимости
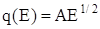
свидетельствует о сближении уровней по мере роста энергии (рисунок 3).
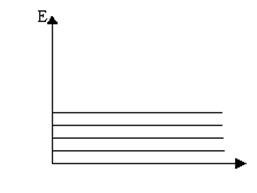
Рисунок 3
Но поскольку эта зависимость довольно слабая, то приведенная оценка является достаточно точной. Теперь становится ясной причина малого вклада электронного газа в общую теплоемкость металла - это малость числа электронов, участвующих в тепловом движении. Этот вклад становится заметным лишь при низких температурах, когда тепловые колебания узлов решетки прекращаются.
Вследствие большой кинетической энергии электронов электронный газ обладает большим давлением. Это давление при абсолютном нуле температуры может быть вычислено по формуле
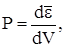
где 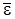 - средняя кинетическая энергия всех электронов в данном образце металла объемом V:
- средняя кинетическая энергия всех электронов в данном образце металла объемом V:
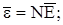
N - число электронов в образце.
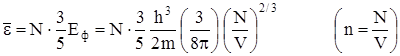
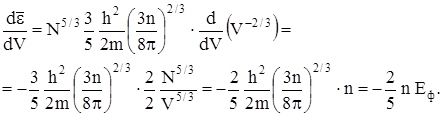
Отсюда
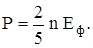 (22)
(22)
Дата добавления: 2016-01-05; просмотров: 87; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
