Пример использования обобщенного решающего правила

Рассмотрим конкретный случай использования ОРП в качестве математического аппарата поддержки принятия решения для данной индивидуальной задачи.

Таблица 12

	F₁(x_r)	F₂(x_r)
x₁
x₂	4,5	4,5
x₃	4,9

Пусть на МДФ Х= {x₁, x₂, x₃} согласно таблице 12, определена ВЦФ F(x) = F₁(x), F₂(x), состоящая из двух минимизируемых критериев F_ν(x) .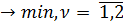

Из табл. 12 , что ПМА и ПМ данной 2-критериальной задачи совпадают с МДР, т.е.

Х⁰= 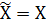= {x_r}, r = .

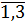При этих исходных данных требуется выбрать ПМА Х⁰решение, обладающее наибольшей полезностью. В качестве математического инструмента поддержки принятия решения используем описанное в параграфе 2.4 ОРП и проранжируем элементы x_r € X⁰, r = 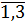в порядке убывания их предпочтительности, т.е. полезности. По предложению ЛПР или заключению экспертов эта полезность может быть косвенно оценена следующими тремя РП:

(12) (62) f₁(x) = 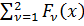- Линейная свертка критериев;

(13) (63) f₂(x) = 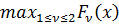- оценка по наихудшему (вида MINMAX);

(14) (64) f₃(x) = (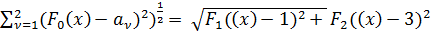 -расстояние до идеальной точки а = (а₁,а₂) = (1,3) эти критерии и представляют собой указанные выше 2-местные функционалы (54) (4).

Реализуя ОРП на базе этих РП, исходим из того, что считается выполненным следующее:

Предположение 1. В каждом РП системы S ={ f_s(x)}, s = 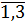критерии F_ν(x) 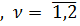рассматриваются как равноправные, т.е. их КОВ₍₂₉₎одинаковы:

ν₁ = ν₂ = 1.В свою очередь все РП f_s(x) € Sтакже обладают одинаковой относительной важностью, так численная оценка каждого из них учитывается в ОРП без умножения на какие-либо весовые коэффициенты.

Переходим к реализации вычислительной схемы ОРП, которая осуществляется поэтапно или итеративно.

Таблица 13

	F₁(x_r)	F₂(x_r)	F₃(x_r)
x₁	7	6	3
x₂	9	4,5	3,8
x₃	7,9	4,9	3,9

Итерация k=1. Для значений критериев F_ν(x) 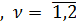,заданных таблицей 12, вычисляем значения РП (12-14) (62)-(64), которые представляем в таблице 13. Согласно этой таблице элементы x_r € X⁰ являются векторно несравнимыми п новой ВЦФОП:

f(x) = (f₁(x), f₂(x), f₃(x)), (15) (65)

которая представляет собой указанную выше ВЦФОП (3) (53),

т.о., результатом первой итерации является множество конкурирующих альтернатив. (МКА) 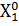,которое совпадает с исходным ПМА Х⁰{x₁, x₂, x₃} = X⁰.Поэтому, для перехода к следующей (второй) итерации пронумеруем компоненты f_s(x), s = 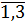новой ВЦФОП (65). Для этого сначала вычислим нормирующие коэффициенты 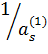; s =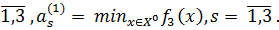

Из табл. 13 имеем: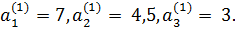

Тогда, = ;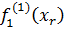

= ;

= .

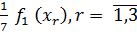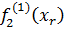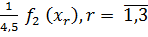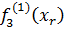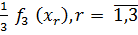Таблица 14

x_r	F₁⁽¹⁾ (x_r)	F₂⁽¹⁾ (x_r)	F₃⁽¹⁾(x_r)
x₁	1	1,33	1
x₂	1,29	1	1,27
x₃	1,13	1,09	1,3

Табл.14 является исходной для следующей итерации.

Итерация k=2. Подставляя нормированные значения 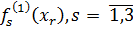, , 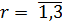заданные табл.14 в формулы (55), (56) и (57), вычисляем значения ВЦФОП (60) для k=1 на :

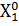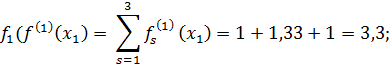
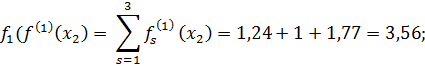
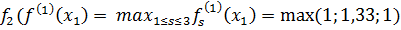= 1,33;

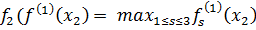= 1,29;

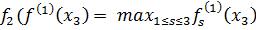= 1,3;

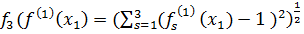= (0²+0,33²+0²)^1/2= 0,33;

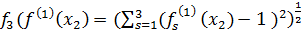= 0,4;

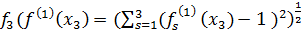= 0,34.

Полученные данные сведем в таблицу 15, которая представляет собой новую ВЦФОП вида (60) на ПМА Х₁⁰:

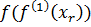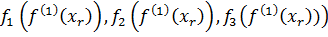= ( (66)

Таблица 15

x_r	F(f₁⁽¹⁾(x_r))	F(f₂⁽¹⁾ (x_r))	F(F₃⁽¹⁾(x_r))
x₁	3,33	1,33	0,33
x₂	3,56	1,29	0,7
x₃	3,52	1,3	0,34

Как видно из таблицы 15, все решения x_r € X₁⁰являются векторно несравнимыми по ВЦФОП (66). Т.о. результатом итерации k=2 является новое ПМА Х₂⁰, совпадающее согласно Х₂⁰ = Х₁⁰. Для перехода к следующей итерации k=3 осуществим нормирование критериев ВЦФОП (66).

Сначала вычислим нормирующие коэффициенты: 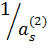используя формулу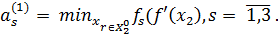

Из табл.15 имеем:

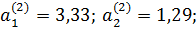
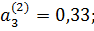
Тогда согласно формуле (59) получаем нормированные значения критериев векторной целевой функции оценки полезностей (60) для k=2:

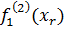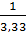= f₁(f(¹⁾(x_r)); r = ;

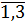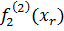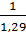= f₂(f(¹⁾(x_r)); r = ;

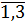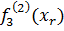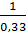= f₃(f(¹⁾(x_r)); r = .

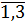Результаты сводим в таблицу 16, которая и представляет исходные данные для следующей итерации.

Таблица 16

F(x) x_r	f₁⁽²⁾ (x_r)	f₂⁽²⁾ (x_r)	f₃⁽²⁾(x_r)
x₁	1	1,03	1
x₂	1,07	1	1,21
x₃	1,06	1,01	1,03

Итерация k=3.

Подставляя нормированные значения 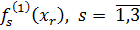, 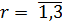по таблице 16 в формулы (55), (56) и (57) вычисляем значения 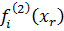, , 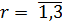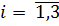получаем табл. 17, которая определяет ВЦФОП на ПМАХ₂⁰.

Таблица 17

F(x) x_r	F₁(f⁽²⁾(x_r))	F₂(f⁽²⁾ (x_r))	F₃(f⁽²⁾(x_r))
x₁	3,03	1,03	0,03
x₂	3,28	1,21	0,22
x₃	3,1	1,06	0,07

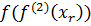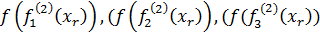= () (67)

Как видно из таблицы 17, все решения x_r € X₂⁰являются векторно сравнимыми по ВЦФОП (67) т.е. достигнутая полная векторная сравнимость элементов x_r € X₂⁰ означает, что эти альтернативы можно проранжировать по убыванию предпочтительности или, более точно, по возрастанию численных значений компонент ВЦФОП (67).

Для рассматриваемой индивидуальной задачи в результате указанного ранжирования получаем последовательность:

x₁ < x₃< x₂ (68)

в соответствии со строгим возрастанием значений ВЦФОП (67):

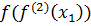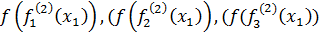= ( = (3,03; 1,03; 0,03) < = ( = (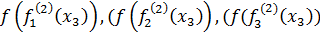3,1; 1,06; 0,07) < 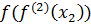= ( = (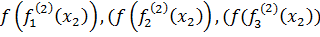3,28; 1,21; 0,22)

Последовательность (68) совместно с конкретными значениями ВЦФОП (69) и составляют основу того, что подразумевается под термином «поддержка принятия решения» для ППР.

Дата добавления: 2016-01-04; просмотров: 9; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!