Нормирование критериев: соизмеримость и сопоставимость численных значений критериев

Нормирование критериев: однородность по виду экстремума

Пусть ЛПР должен использовать то или другое методическое и математическое обеспечение для выбора и принятия решения в индивидуальной N-критериальной задаче с ВЦФ

=(, , … ),

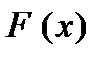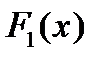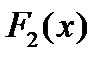которая в данном МДР 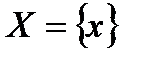определяет собой ПМ 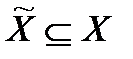. Вопросы нормирования критериев 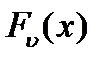данной ВЦФ возникают в случае невыполнения следующих условий:

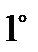^.Однородность по виду экстремума: либо все критерии данной ВЦФ являются минимизируемыми, либо все они являются максимизируемыми.

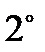. Соизмеримость: все критерии данной ВЦФ имеют одну и ту же единицу измерения.

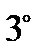. Сопоставимость численных значений критериев: единицы величин 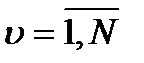отражают одинаковый вклад локальных полезностей этих величин в интегральную полезность данной ВЦФ. Термин «нормирование» критериев данной ВЦФ означает соответствующие преобразования их к виду, удовлетворяющему указанным условиям - .

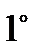Пусть ВЦФ представлена в виде

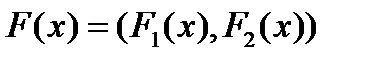, где

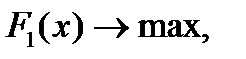
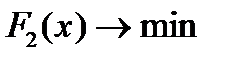Будем предполагать, что условие 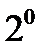“соизмеримость” критериев выполняется. Для устранения невыполнимости требованию

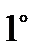. (однородность) можно критерий 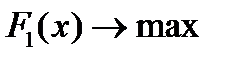преобразовать к виду следующим образом: ,

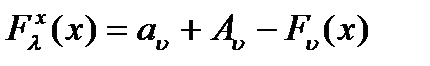
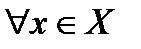где ,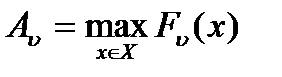

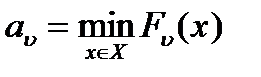
При этом, что очень важно, выполняются следующие условия:

а) для 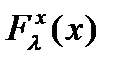— сохраняется также единица измерения, что и для ;

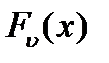б) для и 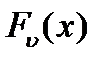сохраняются значения их экстремумов, т.е. , .

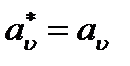в) для всякой пары 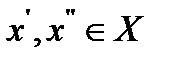выполняется равенство .

В результате преобразования (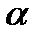), мы придем к ЦФ 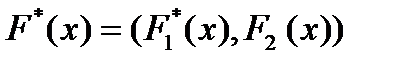, оба критерия которых удовлетворяют условию .

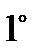Невыполнения условия 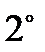можно устранить прономировав каждый из критериев 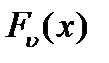:сначала для каждого критерия выбирается эталон 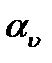(это м/б 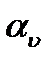или , либо подходящее значение критерия ;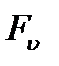

После выбора эталона, критерий F_ν(x)представляется в нормированном (удельном) виде F_ν (x) = 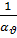F_ν(x), (ν = 1,2,…,N).

На практике встречаются задачи, при решении которых, далее при выполнении условий одинаковой важности критериев, каждый из четырех РП f_s(x); (s = 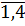)определяемых выражениями (2.1), (2.2), (2.3), (2.4) в одинаковой степени отражает величину полезности вариантов x_r € 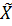. В результате получаем множество конкурирующих альтернатив:

(MKA)X^*= X^*(S) 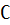X⁰, где

S = {f₃(x)} · s = 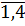, │X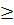^*│ 2.

Полученное MKA содержит более 1-й альтернативы и требуется пополнить имеющуюся систему S новыми подходящими математическими и методологическими средствами для установления бинарного отношения ……..: для пары x', x'' € X^*обосновать ответ на вопрос о том, как соотносятся мера полезностей V этих альтернатив V (x') 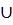V (x''). Один из методов такого ранжирования элементов и MKA известен под названием «обобщенное решающее правило».

Дата добавления: 2016-01-03; просмотров: 41; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!