Теорема 2.3. (свойства обратного отображения)
Лекция 2. Соответствия и функции
План лекции
2.1. Соответствия
2.2. Функции
Соответствия
В начале изложения материала рассмотрим примеры соответствий, изучаемых в начальном курсе математики.
ПРИМЕРЫ
1. а) (17 – 1):4; б) (12 + 18):(6-6); в) 2´7 + 6.
2. а) 2+х =6; б) х-7=4; в) 2х=8.
В первом примере мы установили соответствие между заданными выражениями и их числовыми значениями. Во втором выяснили, какое число является решением уравнения.
Все эти соответствия имеют общее – во обоих случаях мы имеем два множества: в первом – это множество из трех числовых выражений и множество N натуральных чисел (ему принадлежат значения данных выражений); во втором – это множество из трех уравнений и множество N натуральных чисел.
Связь (соответствие) между этими множества можно представить наглядно, при помощи графов.
| а· б· в· |
| ·4 ·20 |
| 1· 2· 3· |
| ·4 ·11 |
Рисунок 2.1 – Наглядное представление соответствия
Полученные множества показывают, что любое соответствие между двумя множествами A и B можно рассматривать как множество упорядоченных пар, образованных из их элементов. А так как упорядоченные пары – это элементы декартова произведения, то приходим к следующему определению общего понятия соответствия.
|
|
|
Определение. Соответствием между множествами А и В называется всякое подмножестводекартова произведения этих множеств 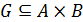 . Соответствия принято обозначать буквами R, P, F, T и др.
. Соответствия принято обозначать буквами R, P, F, T и др.
Способы задания соответствий
Поскольку соответствие – это подмножество, то его можно задать как любое множество, то есть либоперечислив все пары элементов, находящихся в заданном соответствии, либо указав характеристическое свойство элементов этого подмножества.
ПРИМЕР.Соответствие между множествами A = {1, 2, 4, 6} и B = {3, 5} можно задать: 1) при помощи предложения с двумя переменными: а < b при условии, что аÎA, bÎB; 2) перечислив пары чисел, принадлежащих подмножеству декартова произведения A´B: {(1,3),(1,5),(2,3),(2,5),(4,5)}. К этому способу задания относят также задание соответствия при помощи графа и графика.
у
| 1·2·4·6·· |
| ·3 ·5 |
5 · · ·
3 · ·
|
|
|
Рисунок 2.2 – Пример
Определение. Если 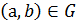 , то говорят, что b соответствует а при соответствии G. Записать это можно следующим образом a G b.
, то говорят, что b соответствует а при соответствии G. Записать это можно следующим образом a G b.
Определение. Множество 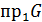 называется областью определения соответствия, множество
называется областью определения соответствия, множество 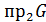 – областью значений соответствия.
– областью значений соответствия.
Определение. Если 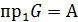 , то то соответствие называется всюду определенным или полностью определенным или инъективным (в противном случае оно называется частичным).
, то то соответствие называется всюду определенным или полностью определенным или инъективным (в противном случае оно называется частичным).
Определение. Если 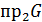 =А, то соответствие называется сюрьективным.
=А, то соответствие называется сюрьективным.
Определение. Множество всех 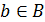 , соответствующих элементу
, соответствующих элементу 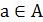 , называется образом b в А при соответствии G. Множество всех элементов а, которым соответствует элемент b, называется прообразом b в А при соответствии G.
, называется образом b в А при соответствии G. Множество всех элементов а, которым соответствует элемент b, называется прообразом b в А при соответствии G.
Определение. Соответствие G называется функциональным (или однозначным), если образом любого элемента из 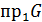 является единственный элемент из
является единственный элемент из 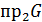 . Соответствие G между А и В называется взаимно однозначным, если оно всюду определено, сюрьективно, функционально, и кроме того, прообразом любого элемента из
. Соответствие G между А и В называется взаимно однозначным, если оно всюду определено, сюрьективно, функционально, и кроме того, прообразом любого элемента из 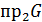 является единств. элемент из
является единств. элемент из 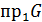 .
.
|
|
|
| Взаимно однозначное соответствие |
| Сюръективное соответствие |
| В |
| А |
| В |
| А |
| В |
| А |
| Инъективное соответствие |
Рисунок 2.3 – Виды соответствий
ПРИМЕР. Круг G радиуса 1 с центром в точке (3, 2), т.е. множество пар действительных чисел (х, у), удовлетворяющих соотношению 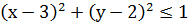 ,
,
задает соответствие между R и R (осью абсцисс и осью ординат).
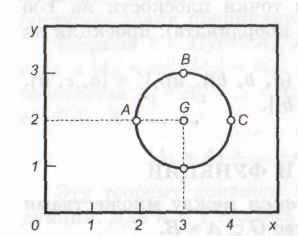
Рисунок 2.4 – Пример соответствия
Образом числа 4 при этом соответствии является единств. число 2, образом числа 3 – отрезок 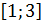 оси ординат. Этот же отрезок
оси ординат. Этот же отрезок 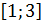 является образом отрезка
является образом отрезка 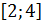 оси абсцисс. Этот же отрезок является прообразом числа 2. Данное соответствие не является функциональным. Примером функционального соответствия между действительными числами служит дуга АВС.
оси абсцисс. Этот же отрезок является прообразом числа 2. Данное соответствие не является функциональным. Примером функционального соответствия между действительными числами служит дуга АВС.
Теорема 2.1. Если между конечными множествами установлено взаимно-однозначное соответствие, то множества равномощны.
Доказательство. Пусть даны два конечных множества А и В, между которыми можно установить взаимно-однозначное соответствие. Допустим противное, что |A|<>|B|, тогда
|
|
|
|A|<|B|, значит дано сюръективное соответствие, но не инъективное, т.е. в множестве В есть два элемента, имеющие один и тот же прообраз;
|A|>|B|, значит дано инъективное соответствие, но не сюръективное, т.е. в множестве А есть два элемента, имеющие один и тот же образ.
В любом случае мы не получаем взаимооднозначности соответствия, что приводит к неверности предположения.
Следствие 1. Конечные множества равномощны, если между ними можно установить взаимно-однозначное соответствие.
Следствие 2. Для бесконечных множеств данное утверждение является определением равномощности.
Определение. Множества, равномощные множеству натуральных чисел, называются счетными.
Утверждение 1. Объединение конечного числа четных множеств счетно.
Теорема 2.2. (Кантора). Множество всех действительных чисел из отрезка [0,1] несчетно.
Утверждение 2. Мощность несчетного множества называется континуум. Булеан счетного множества континуален, поскольку его можно сопоставить во взаимно-однозначное соответствие с отрезком [0,1].
Функции
Определение. Функцией называется функциональное соответствие. Если функция f устанавливает соответствие между множествами А и В, то говорят, что функция f имеет тип 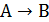 (обозначение
(обозначение 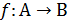 ).
).
Каждому элементу а из своей области определения функция f ставит в соответствие единственный элемент b из области значений. Это обозначается известной записью f(a)=b.
Определение. Элемент а называется аргументом функции, b – значением функции на а.
Пусть f: A®B, тогда
множество определения функции: 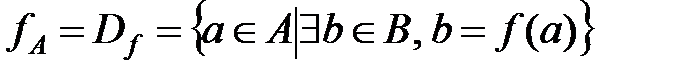 ;
;
множество значений функции: 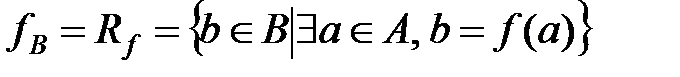 .
.
Множество определения функции является подмножеством области определения, т.е. Df Í A, а множество значений функции является подмножеством области значений функции, т.е. Rf Í B.
Определение. Если Df = A, то функция называется тотальной, а если Df ≠ A - частичной функцией.
Определение. Полностью определенная функция 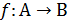 называется отображением А в В.
называется отображением А в В.
Образ А при отображении f обозначается f(A).
Определение. Отображение типа 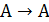 называется преобразованием множества А.
называется преобразованием множества А.
Диаграмма Венна служит удобной иллюстрацией функции, определенной на множестве A со значениями в множестве B.

Рисунок 2.5 – Функция, определенная на множестве A со значениями в множестве B.
ПРИМЕР. Дано отображение f: Q®Z, где f ( x )= x3-5 для всех xÎQ (Q – рациональные числа, Z – целые числа).
Найти: 1) образ элемента 1;
2) прообраз f (3); f (5).
РЕШЕНИЕ.
1) Сначала надо убедиться, что 1ÎQ. Это так.
Чтобы найти образ элемента, достаточно в отображение подставить вместо x число 1. Получаем, f(1)=13-5= - 4. - 4ÎZ. Значит, элемент 1 имеет образ, и он равен - 4.
2) Сначала убедимся, что 3ÎZ. Это так.
Чтобы найти прообраз, вместо f ( x ) подставляем 3, и решаем уравнение: x3-5=3. Получаем, x=2. Причем 2ÎQ. Значит, f (3)=2.
По аналогии находим прообраз 5. Решаем уравнение x3-5=5, и получаем 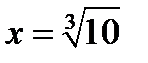 . Но
. Но 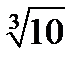 ÏQ. Значит, f (5)=Æ.
ÏQ. Значит, f (5)=Æ.
Определение. Функции f и g равны, если их область определения – одно и то же множество А и для любого элемента 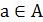 f(a)=g(a).
f(a)=g(a).
ПРИМЕРЫ.
1) Функция f(x)=2х является отображением множества R всех действ. чисел на множество R+ всех положительных действ. чисел.
2) Функция f(x)=arctgx – отображение множества R на интервал 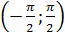 .
.
Определение. Функция 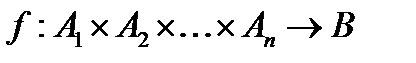 называется функцией n аргументов, или n-местной функцией. Такая функция отображает кортеж
называется функцией n аргументов, или n-местной функцией. Такая функция отображает кортеж 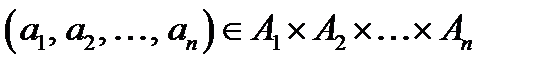 в элемент bÎB,
в элемент bÎB, 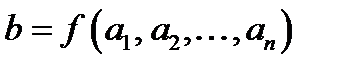 .
.
Сложение, умножение, вычитание, деление является двухместными функциями на R, т.е. функциями типа R2 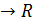 .
.
Свойства отображений (функций).
1) Отображение f: A®B называется инъективным, если оно различные элементы из A отображает в различные элементы из B: 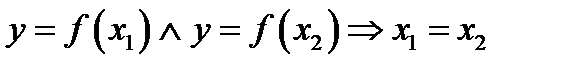 .
.

Рисунок 2.6 – Инъективное отображение
2) Отображение f: A®B называется сюръективным или отображением на все множество B, если в каждый элемент множества B отображается хотя бы один элемент из A: 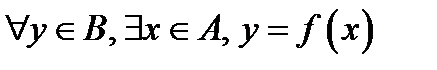 .
.

Рисунок 2.7 – Сюръективное отображение
3) Отображение f: A®B, которое одновременно инъективно и сюръективно, называется биективным или взаимнооднозначным отображением множества A на множество B.
ПРИМЕР. Пусть дано отображение f: R®R, которое определено таким образом, что 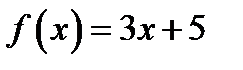 . Выяснить, какими свойствами обладает это отображение.
. Выяснить, какими свойствами обладает это отображение.
РЕШЕНИЕ. Даная функция инъективна, т.к. если f (x1) = f (x2), тогда 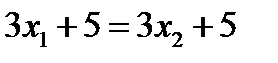 и, следовательно, x1=x2.
и, следовательно, x1=x2.
Функция f является также сюръекцией. Для любого действительного числа y требуется найти такое x, что f (x)=y=3x+5. Решая это уравнение относительно x, находим, что если 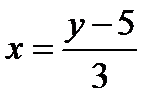 , тогда f (x)=y.
, тогда f (x)=y.
Поэтому f представляет собой взаимно однозначное соответствие. А, значит, является биекцией.
ПРИМЕР. Пусть дано отображение f: R®R, которое определено таким образом, что 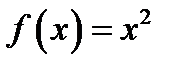 . Выяснить, какими свойствами обладает это отображение.
. Выяснить, какими свойствами обладает это отображение.
РЕШЕНИЕ. Функция f не является инъективной, т.к. f (2)=f (-2), но 2¹ -2.
Функция f не является также и сюръективной, поскольку не существует такого действительного числа x, для которого f (x)= -1.
Определение. Пусть дано соответствие 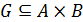 . Если соответствие H
. Если соответствие H 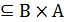 таково, что
таково, что 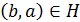 т. и т.т., когда
т. и т.т., когда 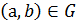 , то соответствие H называется обратным к G и обозначается G-1. Соответствия G и G-1 называют взаимно обратными.
, то соответствие H называется обратным к G и обозначается G-1. Соответствия G и G-1 называют взаимно обратными.
Определение. Если соответствие, обратное к функции 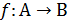 , явл-ся функциональным, то оно называется функцией, обратной к f и обозначается f -1.
, явл-ся функциональным, то оно называется функцией, обратной к f и обозначается f -1.
Так как в обратном соответствии образы и прообразы меняются местами, то для существования функции, обратной к 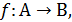 требуется, чтобы каждый элемент b из области значений f имел единственный прообраз. Это означает, что для функции
требуется, чтобы каждый элемент b из области значений f имел единственный прообраз. Это означает, что для функции 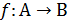 обратная функция существует тогда и только тогда, когда F является взаимно однозначным соответствием между своей областью определения и областью значений.
обратная функция существует тогда и только тогда, когда F является взаимно однозначным соответствием между своей областью определения и областью значений.
Теорема 2.3. (свойства обратного отображения)
Если f: A®B – биекция, то
1) 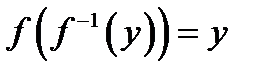 для любого y из B;
для любого y из B;
2) 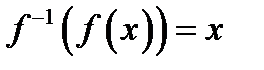 для любого x из A.
для любого x из A.
Доказательство.
1) Пусть yÎB. Так как биекция сюрьективна, то $ 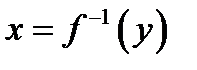 . Такой x единственен и f(x)=y. Имеем:
. Такой x единственен и f(x)=y. Имеем:  .
.
2) Аналогично доказывается, что 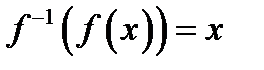 для любого x из A.
для любого x из A.
ПРИМЕРЫ.
1. Функция sinx имеет тип 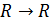 . Отрезок
. Отрезок 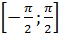 на отрезок
на отрезок 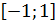 . Поэтому на отрезке
. Поэтому на отрезке 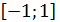 для нее существует обратная функция arcsinx.
для нее существует обратная функция arcsinx.
2. Для кодирующей функции обратной будет декодирующая функция, которая каждому коду ставит в соответствие закодированный этим кодом объект.
Определение. Композицией (суперпозицией, произведением) отображений f: A®B и g: B®C называется отображение h: 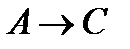 , которое записывается h = g o . f
, которое записывается h = g o . f
Следует отметить, что 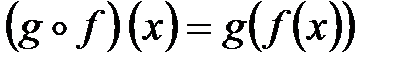
ПРИМЕР. Рассмотрим две функции
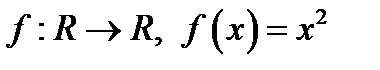 и
и 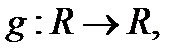
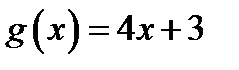 .
.
Найти: 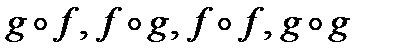 .
.
РЕШЕНИЕ. Все четыре новые функции определены на R со значениями в R.
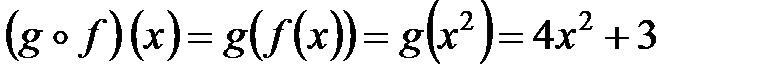 ;
;
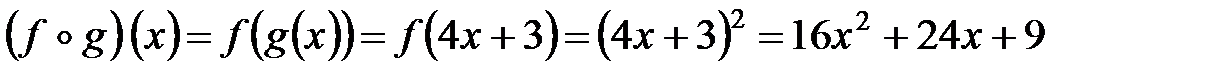 ;
;
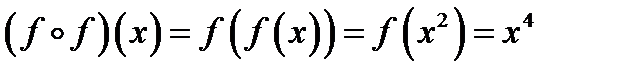 ;
;
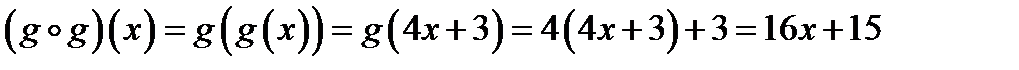 .
.
Дата добавления: 2022-12-03; просмотров: 98; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
