КЛАССЫ ВЫЧЕТОВ ПО ИДЕАЛУ КОЛЬЦА

Глава Iv. Кольца и поля

ОПРЕДЕЛЕНИЕ КОЛЬЦА

Одним из центральных понятий современной алгебры является понятие кольца.

Определение. Пусть К - множество, в котором заданы два алгебраических действия. Одно будем называть сложением, и обозначать “+”, второе будем называть умножением и обозначать “´“. Множество К с действиями сложения и умножения называется (ассоциативным) кольцом, если выполняются следующие условия:

1) сложение коммутативно, ассоциативное обратимо;

2) умножение ассоциативно;

3) сложению и умножение связаны двумя дистрибутивными законами: "a, b, cÎK(a ´(b+c)=a´b+a´c, (a+b)´c=a´c+b´c).

Будем обозначать К=(К,+,´) - кольцо. Можно дать аксиоматическое определение кольца:

Определение. Алгебру К=(К,+,´) будем называть кольцом, если для элементов множества К выполняются следующие аксиомы:

А0 (аксиома замкнутости по сложению) "a,bÎK$!cÎK(c=a+b)

А1 (аксиома ассоциативности сложения) "a,b,cÎK(a+(b+c)=(a+b)+c)

А1’ (аксиома коммутативности сложения) "a,bÎK(a+b=b+a)

А2 (аксиома обратимости сложения)

1° $0ÎK"aÎK(a+0=a)

2° "aÎK$-aÎK(a+(-a)=0)

М0 (аксиома замкнутости по умножению) "a,bÎK$!cÎK(c=ab)

М1 (аксиома ассоциативности умножения) "a,b,cÎK(a(bc)=(ab)c)

D (аксиома дистрибутивности)

"a,b,cÎK(a(b+c)=ab+ac Ù (b+c)a=ba+ca)

Примеры :

1. Множество целых чисел Z образует кольцо.

2. Числа вида a+bÖp, где а, b - целые числа, р - простое число, образуют кольцо.

3. Множество целых чисел, делящихся на данное число n, является кольцом

4. Множество натуральных чисел кольцом не является.

5. Множество всех многочленов относительно сложения и умножения образует кольцо.

6. K={а₁, a₂, a₃). Действие сложения и умножения заданы следующими таблицами:

+	a₁	a₂	a₃	´	a₁	a₂	a₃
a₁	a₂	a₃	a₁	a₁	a₁	a₂	a₃
a₂	a₃	a₁	a₂	a₂	a₂	a₁	a₃
a₃	a₁	a₂	a₃	a₃	a₃	a₃	a₃

Необходимо доказать, что K=(K,+,×) является кольцом. Таблицы определяют действие в К. Остается проверить выполнение свойств, указанных в определении кольца. (Проверить самостоятельно.) Отметим, что нулем в данном кольце является элемент а₃, что видно из определения действия сложения.

Так как кольцо является коммутативной группой по сложению, то для любых элементов а и b кольца уравнение b+х=а имеет единственное решение а + (-b), которое обозначается также через а- b и называется разностью элементов а и b. Абелеву группу (K,+) называют аддитивной группой кольца, а полугруппу (K,×) – мультипликативной полугруппой кольца. Если 1ÎК, тогда К называется кольцом с единицей. Кольцо К будем называть коммутативным кольцом, если операция умножения в К коммутативна.

Простейшие свойства кольца

Для любых элементов а, b , с кольца К=(К,+,×) имеет место:

1) если a+b=a, то b=0;

2) если a+b=0, то b=-a;

3) -(-а)=а;

4) 0×а=а ×0=0;

5) (-а). b =а.(- b)=-(а b);

6) (-а)(-b)=а b;

7) (а- b)×с=а ×с- b×с и с×(а- b)=с×а - с× b ;

8) (a₁+a₂+…+a_n)(b₁+b₂+…+b_m)= ;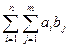

9) если К – коммутативное кольцо, тогда

"a,bÎK"nÎN((a+b)ⁿ= , где .

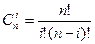Доказательство

1. Если a+b=a, то b=0+b=(-a+a)+b=-a+(a+b)==-a+a=0.

2. Если a+b=0, то b=0+b=(-a+a)+b=-a+(a+b)==-a+0=-a.

3. В группе кольца К по сложению (-а)+(-(-а))= -а+а. Отсюда следует равенство -(-а)=а.

4. В силу дистрибутивности умножения относительно сложения 0 × а+0 × а=(0+0) × а=0 × а, то есть 0 × а+0 × а=0 × а. В силу аксиомы А2 из последнего равенства следует 0×а=0.

5. В силу свойства 4 и дистрибутивности умножения относительно сложения а × b +(-а) × b =(а+(-а)) × b =0 × b =0, то есть а × b +(-а) × b =0. Отсюда в силу аксиомы М2 следует (-а)× b =-(а b ).

Аналогично доказывается, что a × (- b )= -( a b ).

6. Из свойств 5 и 3 следует (-a)(-b)=-((-a)b)=-(-ab)=ab.

7. В силу свойства 5 и дистрибутивности умножения относительно сложения (а- b ) × с=(а+(- b )) × с=а × с+(- b ) × с=а × с- b × с. Аналогично доказывается, что с(а- b )=с × а-с × b .

Свойства 8 и 9 доказать самостоятельно.

Определение. Пусть К=(К,+,×,1) и К'=(К',Å,Ä,1') - кольца. Говорят, что отображение j множества К в К' сохраняет операции кольца К, если выполнены условия:

1) "а,bÎK (j(a+b)=j(a)Åj(b));

2) "a , b ÎK (j(a × b)=j(a )Äj(b));

Определение. Гомоморфизмом кольца К в (на) кольцо К' называется отображение множества К в (на) К', сохраняющее все операции кольца.

Гомоморфизм кольца к на кольцо к' называется эпиморфизмом.

Гомоморфизм j кольца к на кольцо к' называется из o морфизмом, если j является инъективным отображением множества К на К', то есть если отображение - биекция.

Кольца K и K' называются изоморфными (К@К'), если существует изоморфизм кольца к на кольцо к'.

Гомоморфизм j кольца к в кольцо к' называется мономорфизмом или вложением, если j является инъективным отображением множества к в к'. Гомоморфизм кольца К в себя называется эндоморфизмом кольца К. Изоморфизм кольца К на себя называется автоморфизмом кольца К. Так, например, автоморфизмом кольца является тождественное отображение кольца на себя.

Гомоморфизм колец обладает следующими свойствами:

1) если j гомоморфизм кольца к в кольцо к' , тогда образом нуля кольца к будет нуль кольца к';

2) если j гомоморфизм кольца к в кольцо к' , тогда образом элемента -аÎ к будет элемент -j(а)Î к';

3) если j гомоморфизм кольца с единицей к в кольцо к' , тогда образом единицы кольца к будет единица кольца к'.

Д оказательство

1. Пусть j(0)Î к' – образ нулевого элемента кольца К. Возьмем произвольный элемент кольца aÎК и найдем его образ j(а)Î к'. Из определения кольца следует, что a+0=0+a=a, тогда так как j - отображение, j(a+0)=j(0+a)=j(a)Ûj(a)+j(0)=j(0)+j(a)=j(a). Последнее равенство означает, что элемент j(0) является нулевым для элемента j(а), а следовательно, и нулем кольца к'.

2,3. Доказать самостоятельно.

Определение. Множество L=(L,Å,Ä,1_L) называется подкольцом кольца K=(К,+,*,1_К), если LÌK и тождественное отображение множества L в К является мономорфизмом кольца L в К.

Легко показать, что любое подкольцо кольца само является кольцом. При этом нуль и единица кольца являются нулем и единицей любого его подкольца. Действительно, пусть L=(L,Å,Ä,1_L) – подкольцо кольца K=(К,+,*,1_К) и 0 – нуль кольца К. В силу условия 1 определения и свойств 1,2, L=(L,Å) – коммутативная группа и 0 – ее нулевой элемент. Умножение в L ассоциативно. Действительно, в силу условия 2 имеем aÄ(bÄc)=a*(b*c)=(a*b)*c=(aÄb) Äc для любых элементов a,b,c из L. Умножение в L дистрибутивно относительно сложения. В самом деле, по определению гомоморфизма получаем

"a,b,cÎL((aÅb)Äc=(a+b)*c=a*c+b*c=aÄcÅbÄc

Ù cÄ(aÅb)=c*(a+b)=c*a+c*b=cÄaÅcÄb.

Следовательно, L – кольцо.

Теорема. Для того, чтобы подмножество L кольца К было подкольцом кольца К, необходимо и достаточно, чтобы выполнялись следующие условия:

1) "a,bÎL (аÅbÎL);

2) "a,bÎL (а-bÎL);

3) "a,bÎL (аÄbÎL);

Доказать самостоятельно.

ИДЕАЛЫ КОЛЕЦ

Пусть к=(к,+,×) - кольцо и J - подмножество множества К. Множество J называется замкнутым в К относительно вычитания, если a-bÎJ для любых элементов а и b из J.

Множество J называется устойчивым относительно умножения справа на элементы кольца К, если akÎJ для любого aÎJ и любого kÎК, то есть если множество J вместе с каждым своим элементом а содержит все его правые кратные ak, где kÎК.

Аналогично определяется множество, устойчивое относительно умножения слева на элементы кольца к.

Множество J называется устойчивым относительно умножения на элементы кольца К, если оно устойчиво относительно умножения справа и слева на элементы кольца К.

Определение. Правым (левым) идеалом кольца К называется любое непустое подмножество множества К, замкнутое в К относительно вычитания и устойчивое относительно умножения справа (слева) на элементы кольца К.

Определение. Двусторонним идеалом кольца К, или просто идеалом кольца К, называется любое непустое подмножество множества К, если оно является одновременно правым и левым идеалом кольца к.

Из определения следует, что любой идеал J кольца К содержит нуль кольца и замкнут относительно главных операций кольца.

Множество {О_К} есть идеал кольца к, называемый нулевым идеалом.

Множество К также есть идеал кольца к. Он состоит из кратных единицы кольца, и поэтому называется единичным идеалом кольца к. Нулевой и единичный идеалы называются тривиальными идеалами кольца.

Идеалы кольца, отличные от тривиальных, называются собственными идеалами кольца к.

Примеры: Пусть z - кольцо целых чисел, K - произвольное кольцо, n фиксированное целое число. Тогда множество nZ={nx½xÎZ} является идеалом кольца Z, множество nK={nx½xÎK} является идеалом кольца к.

Операции над идеалами

1. Пересечением идеалов I и J кольца K называется множество IÇJ.

2. Суммой идеалов I и J кольца K называется множество

I+J={x+y½xÎI, yÎJ}.

3. Произведением идеалов I и J кольца K называется множество

I×J={x₁y₁+x₂y₂+…+x_ny_n½x_iÎI, y_iÎJ, nÎÀ}

Предложение. Произведение, сумма и пересечение идеалов кольца являются снова идеалами этого же кольца. (Доказать самостоятельно.)

Пусть к - коммутативное кольцо и а - фиксированный элемент этого кольца. Множество {ka½kÎK}=(a), состоящее из кратных элемента а, есть идеал, он называется главным идеалом кольца К, порожденным элементом а.

Предложение. В кольце целых чисел Z каждый идеал является главным.

Доказательство. Пусть J - произвольный идеал в кольце Z. Если J=(0), то доказывать нечего. Если же в J есть еще элемент а¹0, то J содержит и элемент -а, один из этих элементов является положительным числом. Пусть b - наименьшее положительное число в идеале J. Если с - произвольное число в идеале J и r - остаток от деления числа с на b, то с=bq+r, 0£r<b. Так как с и b принадлежат идеалу J, то c-bq=rÎ J. Так как 0£r<b, то г=0, потому что b - наименьшее положительное число идеала J. Следовательно, с=qb, то есть все числа идеала J являются кратными числа b. Отсюда следует, что J=(b), следовательно, J - главный идеал.

КЛАССЫ ВЫЧЕТОВ ПО ИДЕАЛУ КОЛЬЦА

Пусть J - некоторый идеал кольца к. Элементы а, b кольца к называются сравнимыми по идеалу J, если a- b ÎJ и обозначаются aº b (J).

Упражнения. Показать, что отношение сравнения по идеалу J в кольце К (на множестве К) является отношением эквивалентности.

Определение. Классы эквивалентности отношения сравнения по идеалу J в кольце К называются классами вычетов по идеалу J, или смежными классами кольца К по идеалу J.

Рассмотрим основные свойства сравнений по идеалу:

1. Из aºb(J) и cºd(J) следует, что a±сºb±d(J).

Доказательство. В самом деле, если (a- b)ÎJ и (с-d)ÎJ, то (a+c)-(b+d)ÎJ и (a-c)-(b-d)ÎJ. Следовательно, a±сºb±d(J).

2. Из aºb(J) и сÎК следует aсºbс(J), сaºсb(J).

Доказательство. Множество J устойчиво относительно умножения на элементы кольца. Следовательно, для любого элемента с кольца J, так как a-bÎJ, то и aс- bсÎJ и сa-сbÎJ.

3. Из aºb(J) следует, что na=nb(J), где nÎZ.

Доказательство. Так как a- b ÎJ, то nа- nb = n(а- b)Î J.

4. Из aºb(J) и сºd(J) следует, что aсºbd(J).

Доказательство. В самом деле, если (a-b)ÎJ и (c-d)ÎJ, то, в силу устойчивости идеала J относительно сложения и умножения на элементы кольца, имеем ac-bd =ac-bc+bc-bd=(a-b)c+b(c-d)ÎJ.

Определение. Множество всех классов вычетов называется фактор-множеством К по идеалу J, что обозначается к/J.

Класс вычетов, содержащий элемент а кольца к, будем обозначать .

Как следует из свойств 1-4, на фактор-множестве к/J можно определить операции таким образом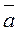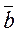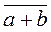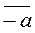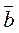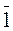: + = , - = , × = , =J для любых элементов и 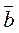из K/J. Такое определение операций в K/J является корректным, так как не зависит от выбора а и b в смежных классах и 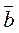соответственно.

Можно доказать, что K/J=(K/J,+,×, 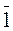) является кольцом, его называют фактор-кольцом кольца К по идеалу J.

ТЕОРЕМА О ГОМОМОРфизМЕ КОЛЕЦ

Пусть К=(К,+,×,1) и К¢=(К¢,+,×,1¢) - кольца, ¦ - гомоморфизм кольца к в кольцо к¢. Обозначим Ker¦={xÎK½¦(x)=0¢}, где 0¢ - нуль кольца К¢. Ker¦ называется ядром гомоморфизма ¦. Покажем, что Ker¦ является, идеалом кольца К. Действительно, Ker¦¹Æ, так как 0Î Ker¦. Для любых а,bÎ Ker¦ имеем ¦(а-b)= ¦(а)-¦(b)=0¢-0¢=0¢, то есть Ker¦ замкнуто в K относительно вычитания. Для любого aÎKer¦ и любого kÎК имеем: ¦(ka)=k¦(a)=k0¢=0¢, то есть kaÎKer¦. аналогично убеждаемся, что akÎ Ker¦. Таким образом, доказано, что Ker¦ есть идеал кольца К. Покажем, что для любых а, b из К равенство ¦(а)=¦(b) выполняется тогда и только тогда, когда = .

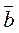Пусть ¦(а)=¦(b), тогда ¦(а-b)= ¦(а)-¦(b)=0¢, так как ¦ - гомоморфизм. Поэтому, а-bÎ Ker¦, откуда = 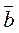. Теперь допустим, что = 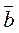. Тогда а-bÎ Ker¦, откуда ¦(а-b)=0¢, так как Ker¦ - ядро. Отсюда получаем: ¦(а)-¦(b)=0¢ и ¦(а)=¦(b).

Теорема. Пусть ¦ - эпиморфизм кольца к на кольцо к¢ с ядром J. Тогда фактор-кольцо к/J изоморфно кольцу к¢.

Доказательство. Пусть K=К/J и K/J=(K/J,+,×, 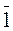), где 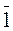=l+J. Обозначим через j отображение K/J в К¢, определенное следующим образом: j( )=¦(а) для каждого элемента из K/J. В силу предыдущих рассуждений значение j( ) не зависит от выбора представителя а в смежном классе . Далее, отображение j сохраняет главные операции кольца к/J. В самом деле, j( 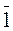)==1_к', и для любых , 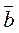из К/J имеем: j( + 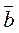)=j( 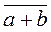)=¦(a+b)= ¦(a)+¦(b) =j( 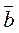)+j( ); j(- )=j( 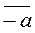)=¦(-a)=-¦(a)=-j( ); j( × )=j( 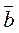) =¦(a×b)=¦(a)×¦(b)= j( )×j( )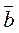

По условию, ¦ отображает К на К¢. Отсюда следует, что j есть отображение множества К на множество К¢. Отображение j инъективно. В самом деле, из равенства j( )=j( 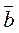) следует ¦(a)=¦(b), откуда = 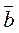. Следовательно, j является изоморфизмом фактор-кольца к/J на кольцо к¢.

ОПРЕДЕЛЕНИЕ ПОЛЯ

Рассмотрим еще одну алгебраическую структуру и дадим ей несколько эквивалентных определений.

Определение. Пусть (Р,+,×) - кольцо, действие умножения в Р обладает свойством коммутативности и для всяких а,bÎР, а¹0 существует такой xÎР, что а×x=b. Тогда (Р,+,×) называется полем.

Определение. Пусть (Р,+,×) – коммутативное кольцо с единицей и для всякого аÎР, а¹0 существует такой а^-1 ÎР, что а×а^-1=1. Тогда (Р,+,×) называется полем.

Определение. Алгебру Р=(Р,+,´) будем называть полем, если для элементов множества Р выполняются следующие аксиомы:

А0 (аксиома замкнутости по сложению) "a,bÎР$!cÎР(c=a+b);

А1 (аксиома ассоциативности сложения) "a,b,cÎР(a+(b+c)=(a+b)+c);

А1’ (аксиома коммутативности сложения) "a,bÎР(a+b=b+a);

А2 (аксиома обратимости сложения);

1° $0ÎР"aÎР(a+0=a);

2° "aÎР$-aÎР(a+(-a)=0);

М0 (аксиома замкнутости по умножению) "a,bÎР$!cÎР(c=ab);

М1 (аксиома ассоциативности умножения) "a,b,cÎР(a(bc)=(ab)c);

М1’ (аксиома коммутативности умножения) "a,bÎР(ab=ba);

М2 (аксиома обратимости умножения);

1° $еÎР"aÎР(aе=a);

2° "aÎР$a^-1ÎР(aa^-1=е);

Д (аксиома дистрибутивности) "a,b,cÎР(a(b+c)=ab+ac ).

Примеры

1. Множество Q является полем

2. Множество Â всех действительных чисел является полем.

Пусть Q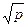= {a+b 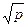½a,bÎQ, р - простое число}. Докажем, что Q- поле.

Определение. Подмножество Р’ поля Р называется подполем поля Р, если относительно операций, определенных в поле Р, множество Р’ само образует поле.

Теорема. Для того, чтобы подмножество Р’ поля Р было подполем поля Р, необходимо и достаточно, чтобы выполнялись следующие условия:

1) "a,bÎP’(a+bÎP’);

2) "a,bÎP’(a-bÎP’);

3) "a,bÎP’(abÎP’);

4) "a,bÎP’(ab^-1ÎP’).

Доказать самостоятельно.

Примеры

1. Множество Q является полем, так как сумма, разность, произведение и частное (если делитель отличен от нуля) двух рациональных чисел является рациональным числом.

2. Множество Â всех действительных чисел является полем.

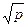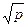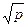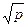4. Пусть Q= {a+b ½a,bÎQ, р -простое число}. Докажем, что Q- поле. Пусть a+b , c+d Î Q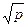, тогда

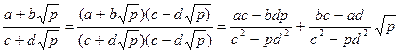но 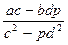и 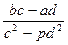числа рациональные, так как множество рациональных чисел является полем. Таким образом, Q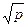является полем.

Упражнения

1. Доказать, что множество ненулевых элементов поля образует группу относительно умножения.

2. В множестве А={а₁, а₂} заданы действия сложения и умножении таблицами:

×	а₁	а₂
а₁	а₁	а₂
а₂	а₂	а₁

+	а₁	а₂
а₁	а₂	а₁
а₂	а₁	а₂

является ли А кольцом, полем?

3. Доказать, что если Р=(Р,+,×) - поле, то в кольце многочленов P[х] каждый идеал является главным.

4. Доказать, что в любом кольце А имеется нуль, то есть элемент 0 такой, что для всякого аÎА имеет место а+0=а, и для него а×0=0.

5. Кольцо классов вычетов по модулю m является полем тогда и только тогда, когда m - простое число. Доказать.

Дата добавления: 2022-12-03; просмотров: 57; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!