Интегрирование некоторых иррациональностей
1) Интегралы вида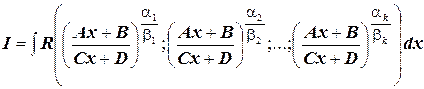 
,
где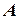 
, 
, 
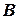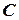и 
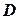- действительные числа; 
- целые числа; 
- целые числа, не равные нулю, а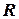 
означает, что выражение рационально относительно своих аргументов.
Произведем замену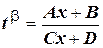 
, где 
.
Тогда
;
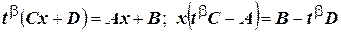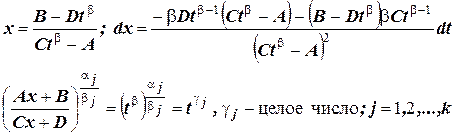
Подставим все эти соотношения в подынтегральное выражение. Получим интеграл от рациональной дроби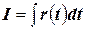 
, который интегрируется с помощью разложения на простейшие дроби.
2) Интегралы вида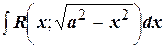 
интегрируется с помощью подстановок 
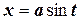или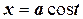 
.
3) Интегралы вида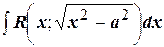 
интегрируется с помощью подстановок 
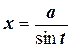или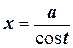 
.
4) Интегралы вида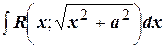 
интегрируется с помощью подстановки 
.
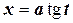5) Интегралывида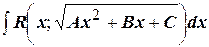 
, причём квадратный трёхчлен 
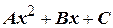не является полным квадратом.
Рассмотрим два случая:
1. Пусть дискриминант квадратного трёхчлена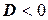 
. Тогда чтобы радикал 
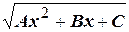существовал в этом случае, необходимо, чтобы 
. Воспользуемся первой подстановкой Эйлера:
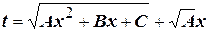(4.15)
Имеем
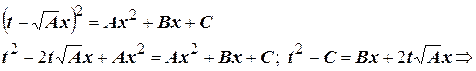
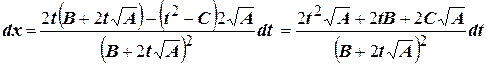
Видим, что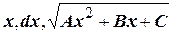 
выражаются через 
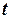и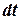 
рационально. Поэтому 
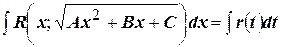, где 
выражение, рациональное относительно .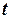
2. Пусть теперь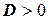 
.
Воспользуемся второй подстановкой Эйлера:
, (4.16)
где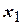 
- один из корней уравнения 
.
.
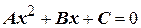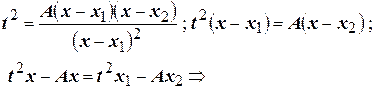
Подставим найденные выражения для 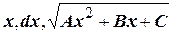в исходный интеграл и получим 
.
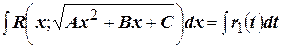Пример: Рационализировать интеграл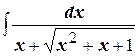 
.
Используем первую подстановку Эйлера: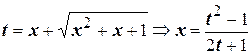 
|
|
|
.
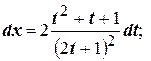
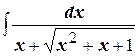
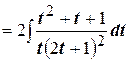Интегрирование биномиальных дифференциалов
Рассмотрим интегралы вида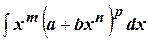 
, где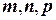 
- рациональные числа. Такие интегралы принято называть интегралами от биномиальных дифференциалов.
Докажем, что подынтегральное выражение рационализируется только в трех случаях:
1) Если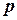 
- целое число.
2) Если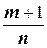 
- целое число.
3) Если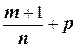 
- целое число.
В самом деле. Положим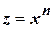 
, тогда 
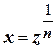. Тогда 
,
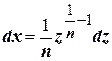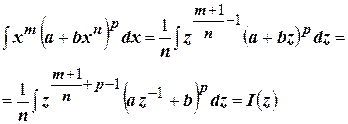(4.17)
Теперь разберем каждый из случаев:
1) Пусть 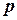- целое число, а 
, 
.
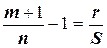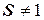Сделаем замену (первая подстановка Чебышёва):
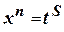4.18)
Тогда 
, а интеграл (4.17) превратится в интеграл от рациональной дроби:
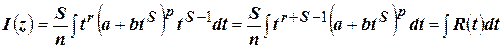
2) Пусть 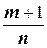- целое число, а 
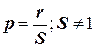. Тогда целым будет и число 
.
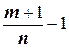Введем замену (вторая подстановка Чебышёва):
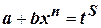(4.19)
В результате получим: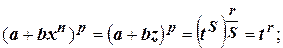 
.
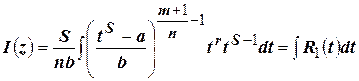3) Пусть теперь 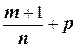- целое число, .
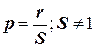Воспользуемся третьей подстановкой Чебышёва:
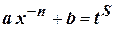. (4.20)
Имеем
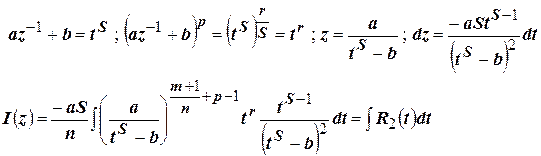
Пример: Рационализировать интеграл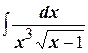 
.
Здесь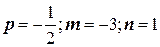 
. Так как число 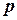нецелое, а 
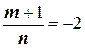, то применим вторую подстановку Чебышёва: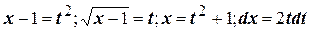 
.
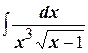
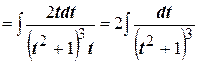Дата добавления: 2022-12-03; просмотров: 49; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!