Полный дифференциал функции двух переменных. Геометрический смысл полного дифференциала.
Вопросы к экзамену
Функция. Область ее определения. Вида областей определения.
Функция – это закон соответствия между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует только одно определенное значение другой величины y (функции или зависимой переменной).
Областью определения функции называется совокупность всех точек числовой оси, в которых она имеет определенные действительные значения. Очевидно, для многих функций областью определения будет не вся числовая ось, а только некоторая ее часть.
Предел функции в точке. Что значит раскрыть неопределенность?
Пределом функции (предельным значением функции) в точке, предельной для области определения функции, называется такая величина, к которой значение рассматриваемой функции стремится при стремлении её аргумента к данной точке.
Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа: (Здесь. — бесконечно малая величина, — бесконечно большая величина, 1 — бесконечно близкое к числу 1 выражение). по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.
|
|
|
Первый и второй замечательные пределы.
Понятие непрерывности функции в точке и на интервале
Понятие разрывной функции. Точки разрыва 1-го и 2-го рода.
Производная функции, ее геометрический смысл.
Производная суммы, произведения и частного двух функций.
Дифференциал функции, Геометрическая интерпретация.
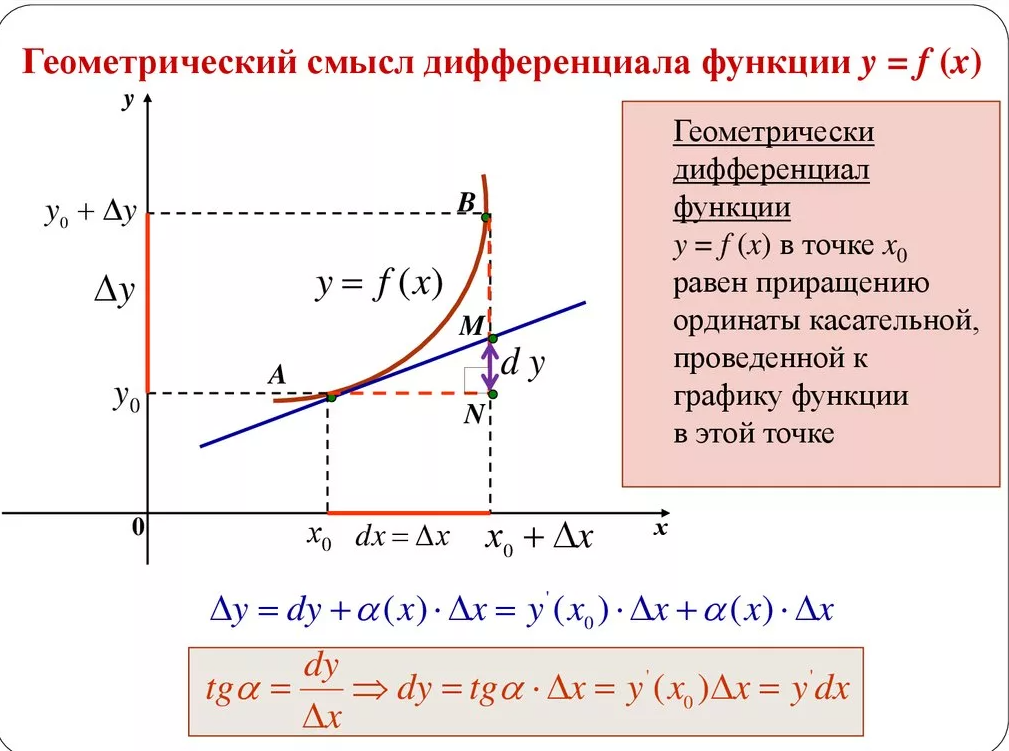
Правило Лопиталя для нахождения пределов.
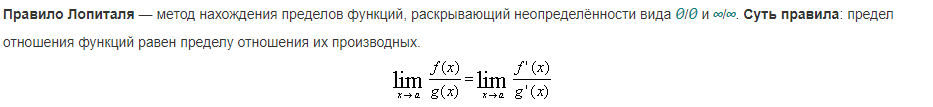
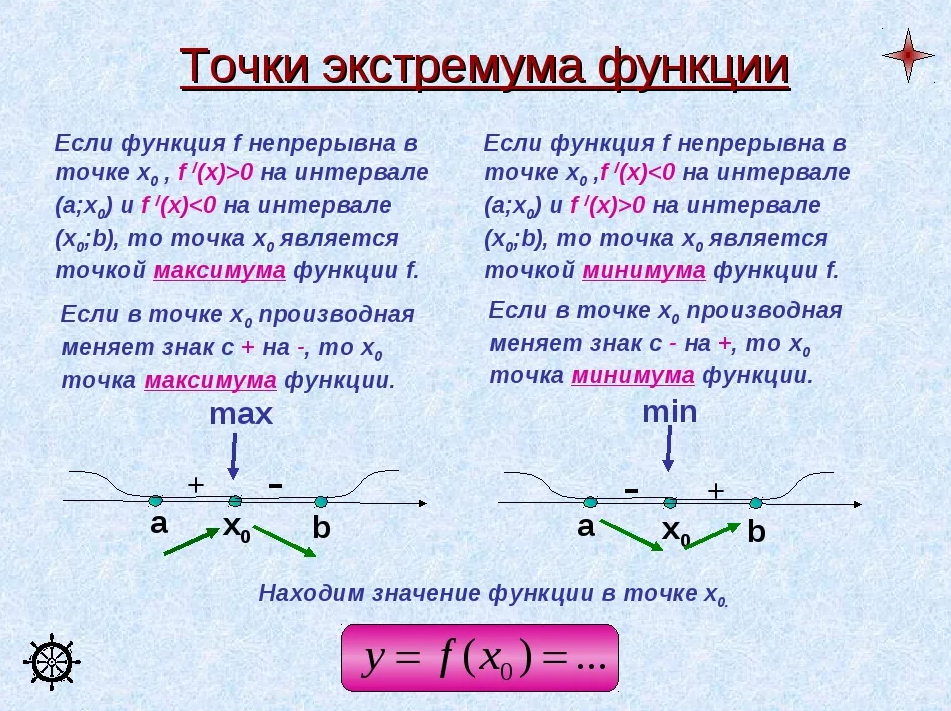
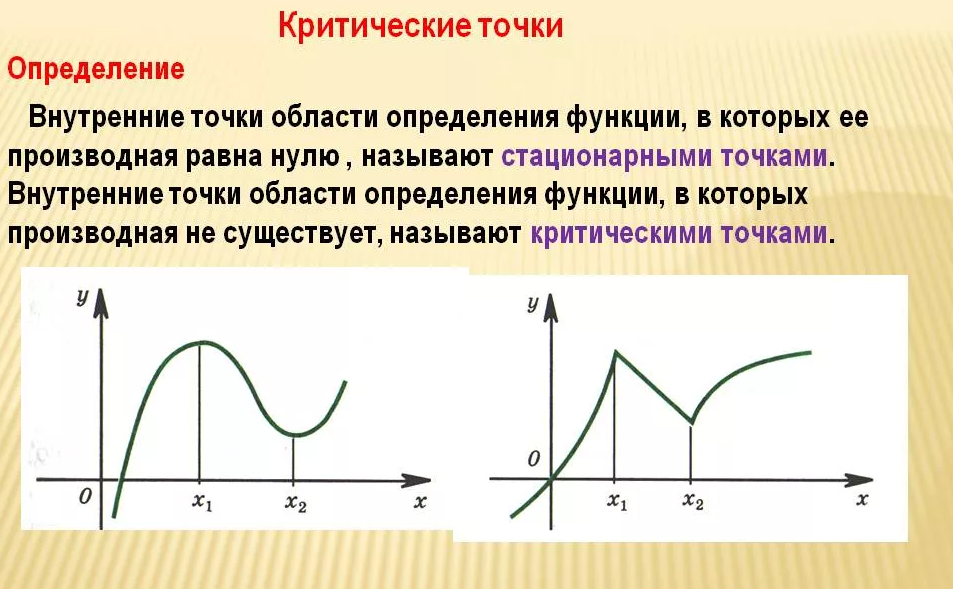
Точки экстремума функции. Критические точки.
Условия возрастания и убывания функции.
Необходимые и достаточные условия существования экстремума.
Условия существования вертикальной и наклонной асимптот. Правило их нахождения.
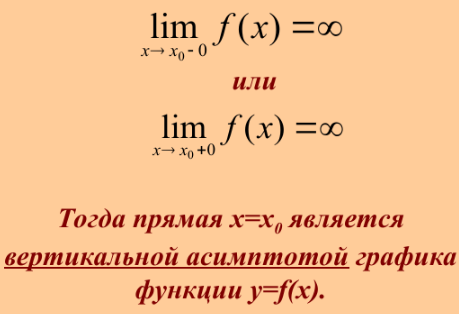
Точки перегиба функции.
Условия выпуклости и вогнутости графика функции.
16. Понятия области определения (существования) функции двух независимых переменных. Граница области. Открытая и замкнутая области.
В простейших случаях область существования функции представляет собой конечную или бесконечную часть координатной плоскости ХОУ, ограниченную одной или несколькими кривыми (граница области). Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой. Примером замкнутой области является круг с окружностью.
|
|
|
Полный дифференциал функции двух переменных. Геометрический смысл полного дифференциала.
18. Частные производные 2-го порядка от функции двух переменных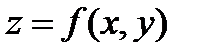 
.
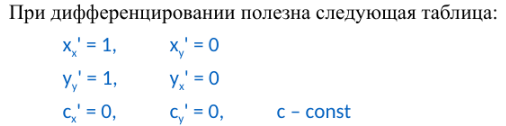
Понятие скалярного поля.
Скалярным полем называется часть пространства, каждой точке которого поставлена в соответствие определённое число – скаляр.
Примеры скалярных полей: 1) поле температур внутри неоднородно нагретого тела; 2) поле давлений воздуха в атмосфере; 3) поле плотности вещества в теле; 4)поле плотности распределения электрического заряда и т.д.
Скалярное поле считается заданным, если в каждой точке M некоторой области W определена скалярная функция U(M). В связи с этим, понятие скалярного поля и функции, определенной в области W, эквивалентны. Если скалярное поле отнесено к декартовой системе координат, то скалярную функцию U(M) можно записать, например, в виде функции двух U(x,y) или трёх U(x,y,z) переменных.
Простейшей геометрической характеристикой скалярного поля U(M) являются поверхности уровня.
|
|
|
Поверхности уровня.
Поверхности уровня – это геометрическое место точек, в которых скалярная функция принимает постоянные значения, т.е. U(x,y,z)=C, где С – произвольная постоянная.
В случае двумерного поля понятие поверхности уровня заменяется понятием линии уровня: U(x,y)=C.
Примеры линий уровня: 1) на топографических картах линии, соединяющие точки, имеющих одну и туже высоту над уровнем моря; 2) в термодинамике на диаграммах состояния линии, соединяющие точки, имеющих одну и туже температуру (изотермы), давление (изобары) или объём (изохоры); 3) в электростатике линии, соединяющие точки, имеющие одинаковый потенциал (эквипотенциальные линии).
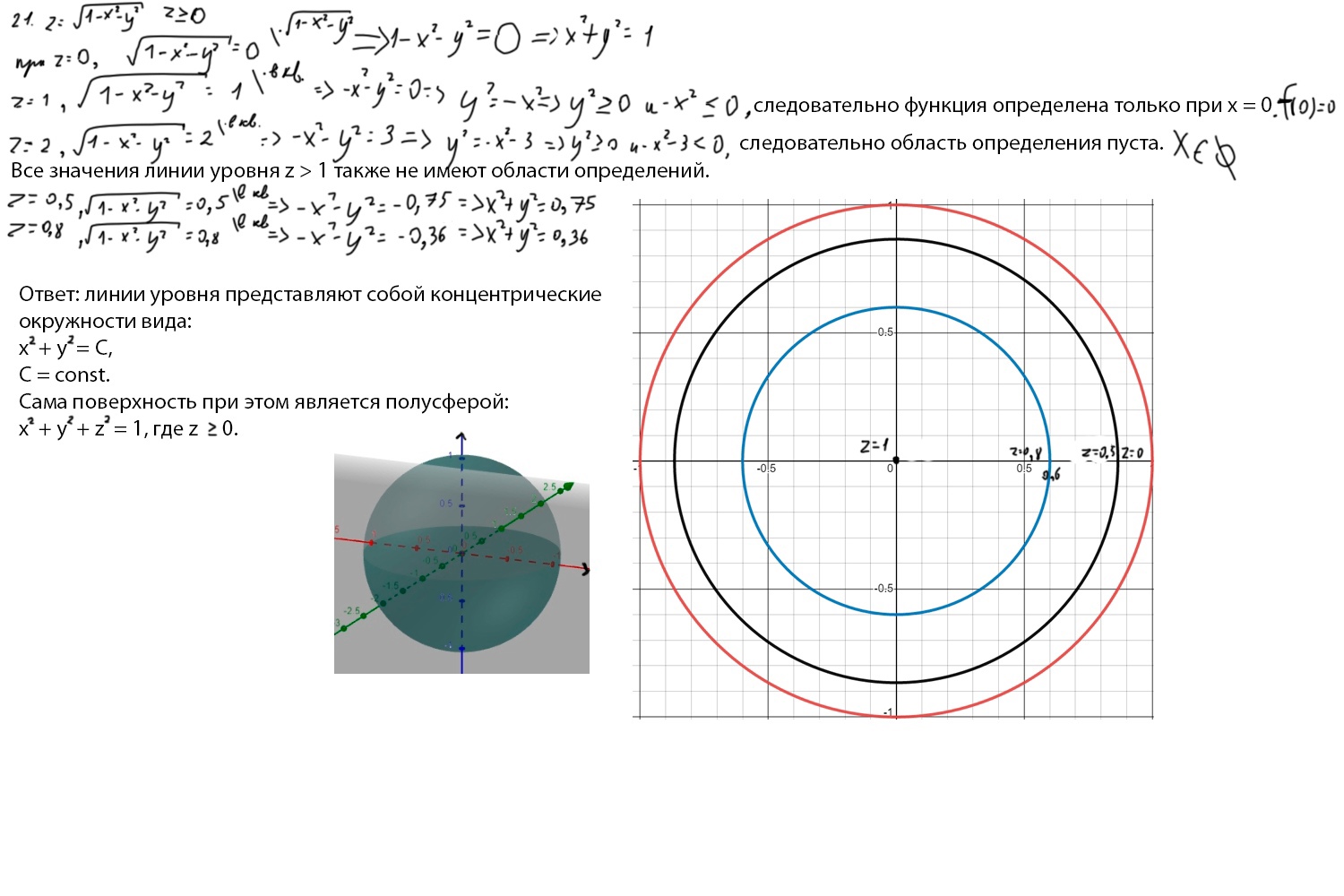
21. Линии уровня (на примере функции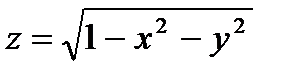 
).
22. Понятие производной от функции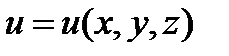 
в точке (х, у, 
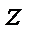) по направлению вектора 
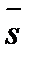.Что она характеризует?
Если мы имеем дело с функцией трёх переменных, то приращения аргументов x, y, z отображаются на осях Оx, Оy, Оz. Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?
И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой прямой, направление которой определяется вектором, произвольно заданным в задаче.
|
|
|
Если рассматривается функция двух или трёх переменных, то два или три измерения задают аргументы, а упомянутая прямая, на которой отображается приращение функции, - это ещё одно измерение и для его акцентирования назовём это измерение не третьим или четвёртым, а нулевым, следуя программистской традиции (в программировании отсчёт чаще начинается не с единицы, а с нуля).
Для того, чтобы перейти к строгому математическому определению производной по направлению, нужно рассмотреть:
1) функцию u = f(M), определённую в окрестности точки M с координатами x, y, z;
2) произвольный вектор l с направляющими косинусами cosα, cosβ, cosγ.
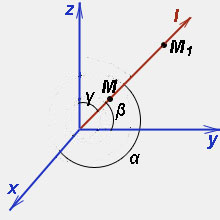
Через точку M проводим прямую, одно из двух возможных направлений которых совпадает с направлением вектора l. На получившейся прямой отметим точку M1, координаты которой образуют суммы координат точки M и приращений соответствующих аргументов функции трёх переменных:
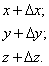
Величину отрезка MM1 можно обозначить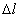 
.
Функция u = f(M) при этом получит приращение
.
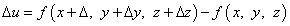23. Понятие градиента функции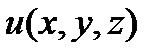 
в точке. Связь между градиентом и производной функции 
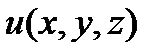в данной точке по любому направлению.
Градиентом функции называется вектор вида
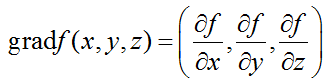
Величина градиента функции, в которой производная имеет наибольшее значение определяется по формуле:
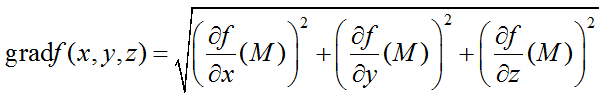
Градиент характеризует скорость изменения функции.
24. Необходимые и достаточные условия экстремума функции 2-х независимых переменных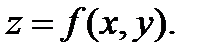 
25. Первообразная. Неопределенный интеграл. Основные свойства.
Дата добавления: 2022-12-03; просмотров: 42; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!