Симплексный метод решения задач линейного программирования
Симплексный метод основывается на следующем:
- область допустимых решений задачи линейного программирования является выпуклым множеством с конечным числом угловых точек, т.е. многогранником или многоугольным множеством;
- оптимальным решением задачи линейного программирования является одна из угловых точек области допустимых решений;
- угловые точки области допустимых решений алгебраически представляют некоторые базисные (опорные) решения системы ограничений задачи.
Данные метод состоит в целенаправленном переборе опорных решений задачи линейного программирования. Он позволяет за конечное число шагов расчёта либо найти оптимальное решение, либо установить его отсутствие.
Симплексные таблицы
Систему ограничений сведем к единичному базису:
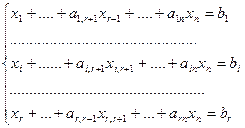
и линейную форму L – к виду
.
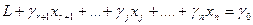В виде таблицы эти данные можно представить так:
| Базисные перемен-ные | Свобод- ные члены | X1 | … | Xi | … | Xr | Xr+1 | … | Xj | … | Xn |
| X1 | b1 | 1 | … | 0 | … | 0 | a1, r+1 | … | a1i | … | a1n |
| … | … | … | … | … | … | … | … | … | … | … | … |
| Xi | bi | 0 | … | 1 | … | 0 | ai, r+1 | … | ai,j | … | ai n |
| … | … | … | … | … | … | … | … | … | … | … | … |
| Xr | br | 0 | … | 0 | … | 1 | ar, r+1 | … | ar,j | … | ar,n |
| L | γ0 | 0 | … | 0 | … | 0 | γr+1 | … | γj | … | γn |
|
|
|
Равенство (**) будем называть приведённым (к свободным переменным) выражением для функции L, а коэффициенты γj - оценками (индексами) соответствующих свободных переменных xj.
1) Выбирается разрешающий столбец ap из условия: оценка γp <0 и хотя бы один элемент aip >0.
2) Выбирается q-я разрешающая строка из условия
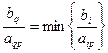для aip >0.
3) Производится пересчёт элементов разрешающей q-й строки по формуле
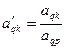(k=0, 1, …, n).
4) Вычисляются элементы всех остальных строк (при k ≠ p) по формуле
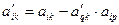(i=0,1, …, q-1, q+1, …, r).
Теорема. Если после выполнения очередной итерации:
1) найдется хотя бы одна отрицательная оценка и в каждом столбце с такой оценкой будет хотя бы один положительный элемент, т.е. γk <0 для некоторых k, и aik >0 для тех же k и некоторого i, то можно улучшить решение, выполнив следующую итерацию:
2) найдётся хотя бы одна отрицательная оценка, столбец которой не содержит положительных элементов, т.е.
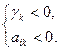
для какого-то k и всех i, то функция L не ограничена в области допустимых решений (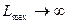 
);
3) все оценки окажутся неотрицательными, т.е.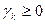 
для всех k, то достигнуто оптимальное решение.
Дата добавления: 2022-12-03; просмотров: 27; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!