Значение невязки необходимо проверять в любом случае, так как ее достаточно малое значение гарантирует достоверность полученного корня.

РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Во многих научных и инженерных задачах возникает необходимость решения уравнений вида

                               f ( x )=0                          (1)

Всякое число, обращающее функцию f(x) в нуль, называется корнем уравнения (1). Нелинейные уравнения подразделяются на алгебраиче­ские и трансцендентные.

Уравнение (1) называется алгебраическим, если функция f(x) является алгебраической или трансцендентным, если функция f(x) не является алгебраической.

Численное решение уравнения (1) обычно проводят в два этапа. На первом этапе необходимо отделить корни уравнения, т.е. найти такие интервалы изменения переменной х, где расположен только один корень (интервалы изоляции корня). На втором этапе проводят уточнение отде­ленных корней, т.е. находят корни с заданной точностью.

Отделение корней

Рассмотрим графический способ отделения корней уравнения (1), который используется, когда отсутствует информация о расположении корней. В интересующей нас области изменения неизвестного (интервал отделения) x Î [ x ₀ , x_n ] вычислим ряд значений левой части уравнения (1) и результаты поместим в табл. 1, по которой можно построить график (рис. 1), из которого следует, что на данном интервале уравнение имеет 3 корня.

Таблица 1
x	f (х)
x0	f0
x1	f1
…	…
xn	fn

 

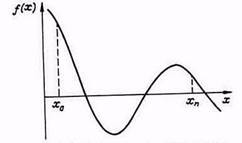
Рисунок 1. График левой части уравне­ния

 

Шаг изменения аргумента х при вычислении табл. 1 выбирается так, чтобы он был меньше расстояния между корнями. Только в этом случае удается отделить все корни.

Автоматизация нахождения интервалов изоляции основана на свойстве интервалов изоляции, заключающемся в различии знаков функции f (х) на их границах. Пример процедуры Roots, реализующей данный подход, приведен ниже. Параметры, передаваемые в процедуру:f-имя функции; а и б-границы интервала отделения; N -количество подинтервалов. Ниже приведен пример отделения корней для уравнения  на отрезке [-0,1;6,5].

 

 

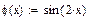
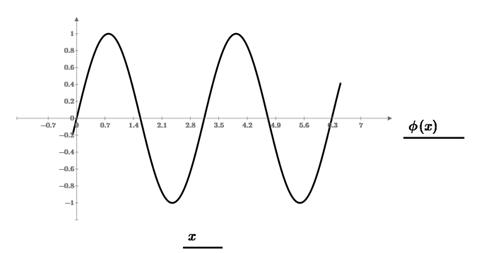
Из графика видно, что на данном интервале уравнение имеет 5 корней.

 

 

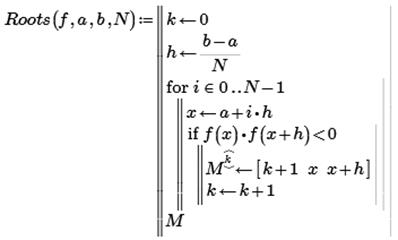
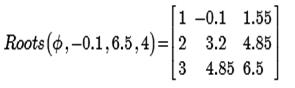
При четырех подинтервалах (крупном шаге) удалось отделить только 3 из 5 корней.

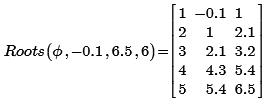
При шести подинтервалах (мелком шаге) удалось отделить все 5 корней.

 

 

Методы уточнения корней

Метод дихотомии

Считаем, что отделение корней уравнения (1) проведено и на интервале изоляции [а, b ] расположен один корень, который необходимо уточнить с погреш­ностью e (рис. 2).

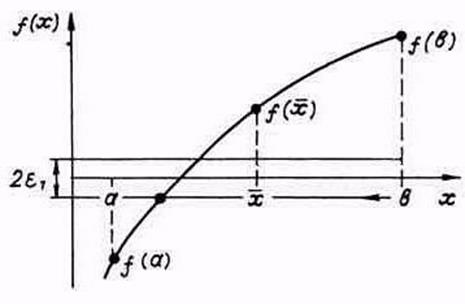
Рисунок 2. Метод дихотомии

Метод дихотомии, или половинного деления, заключается в следующем. Определяем середину отрезка [а, b ]: 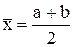 и вычисляем функцию 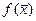. Далее делаем выбор, какую из двух частей отрезка взять для дальнейшего уточнения корня. Если левая часть уравнения f ( x ) есть непрерывная функция аргумента х, то корень будет находиться в той половине отрезка, на концах которой f ( x ) имеет разные знаки. На рис. 3 это будет отрезок [а, 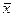], т.е. для очередного шага уточнения точку b перемещаем в точку  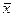и продолжаем процесс деления как с первоначальным отрезком [а, b ].

Итерационный (повторяющийся) процесс будем продолжать до тех пор, пока интервал [а, b ] не станет меньше заданной погрешности e:

| x_n - x_{n -1} |< e

или когда значения функции f ( x ) (невязки) не станут достаточно малы

| f ( x_n )|< e ₁

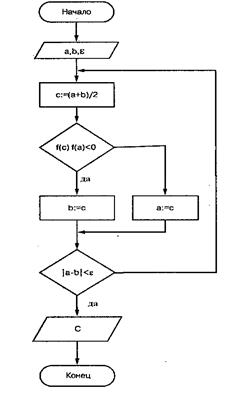
Рисунок 3. Алгоритм метода дихотомии

Значение невязки необходимо проверять в любом случае, так как ее достаточно малое значение гарантирует достоверность полученного корня.

Метод простых итераций

Классический метод

Исходное уравнение f ( x )=0 всегда можно преобразовать к равносильному уравнению, прибавив к обеим его частям х

х = j (х)                                                       (2)

Пусть известно начальное приближение к корню х = x ₀, тогда подставим его в правую часть уравнения (2) и получим новое приближение x ₁ = j (х₀), затем аналогичным образом получим x ₂ = j (х₁) и так далее. Таким образом, итерационное уравнение метода простых итераций имеет вид:

x_{k +1} = j (х _k )                                                       (3)

Необходимо установить, при каких условиях итерационный процесс (3) будет сходиться к корню уравнения х*.

Построим графики двух функций:

y₁(x)=x

y₂(x)= j (x)

Координаты пересечения графиков этих функций и дадут корень исходного уравнения (1) х*.

 

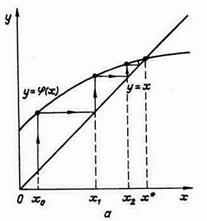
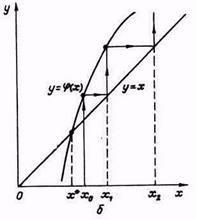
Рисунок. 4. Метод простых итераций:

а - сходящийся процесс ( );

б - расходящийся процесс ( ).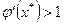

Рассмотрим процесс графически (рис.4). Из графиков видно, что возможны как сходящиеся, так и расходящиеся итерационные процессы. Для того чтобы итерационный процесс был сходящимся, должно выполняться условие

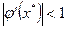                                                                         (4)

Очевидно, классический метод не всегда обладает сходимостью, поэтому потребовалось его усовершенствование.

Усовершенствованный метод итераций

Умножим левую и правую части уравнения (1) на произвольную константу 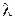 и добавим к обеим частям неизвестное х. При этом корни исходного уравнения  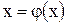не изменятся, где

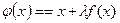                                                                                         (5)         

Надлежащий выбор константы 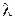 позволит обеспечить выполнение условия сходимости (4). Необходимо выбрать величину  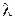такой, чтобы .

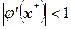Если функция j (х) выбрана в виде (5), то ее производная по х будет

j ’(х) = 1+ 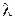f’(х)

Т.е. условие (4) имеет вид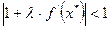

или

             

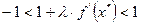
или

             

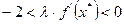
Поэтому константу 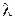 необходимо выбирать из следующих условий:

А) если f ’(х)>0

          -2/ f ’(х*)< 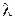<0

Б) если f ’(х)<0

          0< 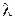<-2/ f ’(х*)

Наибольшую скорость сходимости получим при j ’(х*)=0, тогда

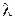 = -1/ f ’(х*).Здесь х*-точка максимального значения модуля производной .

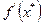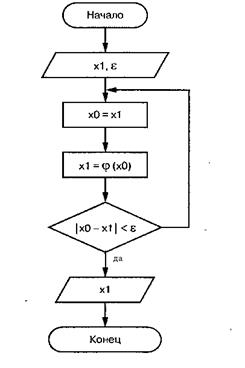
Рисунок 5. Алгоритм ре­шения методом простых итераций

Метод итераций обладает более высокой скоростью сходимости по сравнению с методом половинного деления.

Метод Ньютона (касательных)

Алгоритм Ньютона можно получить с помощью разложения в ряд Тейлора левой части уравнения f ( x ) вблизи корня x_k.

f (х) = f '( x_k )( x - x_k )+ f ( x_k )+…

Пренебрегая членами второго и более высоких порядков и из условия, чтобы в результате следующей итерации функция была равна нулю:

f ( x_{k +1} )=0

получим уравнение f ( x_{k +1} ) = f '( x_k )( x_{k +1} - x_k )+ f ( x_k )=0

Отсюда .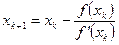

 Рассмотрим графическую иллюстрацию метода (рис. 6). Предположим, что графическим методом определено начальное приближение х₀ к корню. В точке x ₀ вычислим левую часть решаемого уравнения f ₀ = f ( x ₀ ), а также производную в этой точке f '( x ₀ ) = tg a . Следующее приближение к корню найдем в точке x ₁ где касательная к функции f ( x ), проведенная из точки (x ₀, f ₀ ), пересекает ось абсцисс. Затем считаем точку х₁ в качестве началь­ной и продолжаем итерационный процесс. Из рис. 1.6 видно, что таким способом можно приближаться к корню х*. При этом с каждой итерацией расстояние между очередным x_{k +1} и предыдущим х _k приближениями к корню будет уменьшаться. Процесс уточнения корня закончим, когда выпол­нится условие | x_{k +1} - x_k |< e , где e - погрешность определения корня.

 

                    

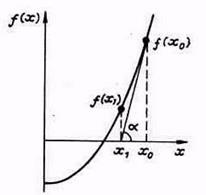
Рис. 6. Метод Ньютона

Метод Ньютона обладает высокой скоростью сходимости. Обычно абсолютная точность решения 10^-5 - 10^-6 достигается через 5-6 итераций.

Недостатком метода является необходимость вычисления на каждой итерации не только левой части уравнения, но и ее производной.

Можно несколько уменьшив скорость сходимости, ограничиться вычислением производной f '( x ) только на первой итерации, а затем вычислять лишь значения f ( x ), не изменяя производной f '( x ). Это алгоритм так называемого модифицированного метода Ньютона (метод Рыбакова) .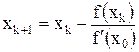 

Метод Ньютона также можно использовать для уточнения корней в области комплексных значений х. В этом случае начальное приближение корня х₀ необходимо выбирать комплексным.

 

Реализация в среде Mathcad

Для решения нелинейных алгебраических уравнений (нахождения корней полиномов) в Mathcad существует функция polyroots(V), где V-вектор коэффициентов полинома. Пример

 

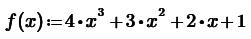
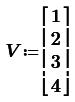
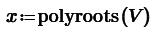
Корни полинома

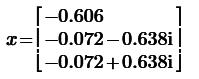
Невязки

 

 

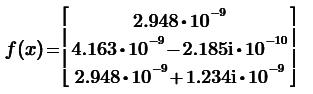
 Для решения трансцендентных уравнений в Mathcad существует функция ROOT(f(x),x[,a,b]). Необязательными параметрами являются границы интервала изоляции корня [a,b]. Если их не указывать, то необходимо перед вызовом данной функции задать начальное приближение для x.

 

---

Дата добавления: 2022-11-11; просмотров: 14; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!