Основные формулы комбинаторики
ЛЕКЦИЯ 1: «ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ»
Понятие о случайном событии
Опыт, эксперимент, наблюдение явления называется испытанием.
Примеры: бросание монеты, бросание игральной кости.
Результат, исход испытания называется событием.
Примеры: выпадение герба, появление того или иного числа очков на брошенной игральной кости.
Для обозначения событий используют большие буквы латинского алфавита: A, B, C и т.д.
Определение 1. Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании.
Пример. Испытание – однократное бросание игральной кости. Событие A – появление четырёх очков, событие B - появление чётного числа очков.
Определение 2. Два события называют несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании.
Пример. Испытание – однократное бросание монеты. Событие A – выпадение герба, событие B - выпадение цифры.
Определение 3. Два события A и B называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит.
Событие, противоположное событию A, обозначают через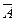 
.
Определение 4. Событие называют достоверным, если в данном испытании оно является единственно возможным его исходом, и невозможным, если в данном испытании оно заведомо не может произойти.
Определение 5. Событие называют случайным, если оно объективно может наступить или не наступить в данном испытании.
|
|
|
Пример. Событие A – выпадение шести очков при бросании игральной кости – случайное.
Можно ли как-то измерить возможность появления некоторого случайного события?
Классическое определение вероятности
Определение 1. Говорят, что совокупность событий образует полную группу событий для данного испытания, если его результатом обязательно становится, хотя бы одно из них.
Примеры: попадание в цель или промах при одном выстреле; выпадение герба и выпадение цифры при одном бросании монеты.
Определение 2. События 
, образующие полную группу попарно несовместимых и равновозможных событий, будем называть элементарными событиями.
Определение 3. Событие A называют благоприятствующим событию B, если наступление события A влечёт за собой наступление события B.
Определение 4 (классическое определение вероятности). Вероятностью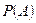 
события A называют отношение 
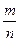числа элементарных событий, благоприятствующих событию A, к числу всех элементарных событий, т.е. 
.
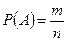Пример. Найти вероятность того, что при бросании игральной кости выпадет чётное число очков (событие A).
n=6; m=3;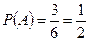 
.
Из классического определения вероятности вытекают следующие её свойства:
|
|
|
1. Вероятность достоверного события равна единице.
Доказательство: m= n, тогда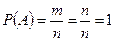 
.
2. Вероятность невозможного события равна нулю.
Доказательство: m=0, тогда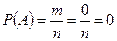 
.
3. Вероятность случайного события есть положительное число, заключённое между нулём и единицей.
Доказательство: 
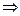
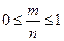
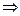
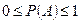
Основные формулы комбинаторики
Комбинаторика – раздел математики, изучающий вопросы о том, сколько комбинаций определённого типа можно составить из данных предметов (элементов).
Определение 1. Размещениями из n различных элементов по m элементов (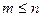 
) называют комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов.
Пример. Из трёх элементов a, b, c можно составить следующие размещения по два элемента: ab, ac, bc, ba, ca, cb.
Число различных размещений без повторений из n элементов по m элементов определяется по формуле: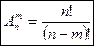 
.
Размещения с повторениями (n различных элементов, элементы могут повторяться):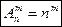 
.
Пример. Возьмем буквы Б, А, Р. Какие размещения из этих букв, взятых по две, можно получить? Сколько таких наборов получиться, если: 1) буквы в наборе не повторяются; 2) буквы могут повторяться?
|
|
|
1) Получатся следующие наборы: БА, БР, АР, АБ, РБ, РА.
.
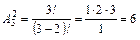2) Получатся наборы: ББ, БА, БР, АА, АБ, АР, РР, РБ, РА.
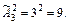
Определение 2. Перестановками из n различных элементов называют размещения из этих n элементов по n.
Перестановки можно считать частным случаем размещений при m= n. Тогда число всех перестановок без повторений из n элементов вычисляется по формуле:
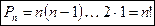
Перестановки с повторениями (k различных элементов, где элементы могут повторяться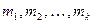 
раз и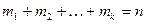 
, где n – общее количество элементов):
.
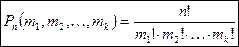Пример. Возьмем буквы Б, А, Р. Какие перестановки из этих букв можно получить? Сколько таких наборов получится, если: 1) буквы в наборе не повторяются; 2) буква А повторяется два раза?
1) Получатся наборы: БАР, БРА, АРБ, АБР, РАБ, РБА.
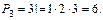
2) Получатся наборы: БАРА, БРАА, БААР, ААРБ, ААБР, АБАР, АРАБ, АРБА, АБРА, РАБА, РААБ, РБАА.
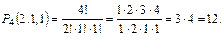
Определение 3. Сочетаниями из n различных элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые отличаются хотя бы одним элементом.
Отметим разницу между сочетаниями и размещениями: в первых не учитывается порядок элементов.
Число сочетаний без повторений из n различных элементов по m элементов вычисляется по формуле: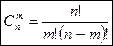 
.
|
|
|
Пример. В лабораторной клетке содержат трёх белых и трёх коричневых мышей. Найдите число способов выбора двух мышей, если они могут быть любого цвета.
m=2, n=6, тогда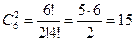 
.
Сочетания с повторениями (n элементов, взятых по m, где элементы могут повторяться):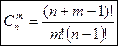 
.
Пример. Возьмем плоды: банан (Б), ананас (А) и репа(Р).Какие сочетания из этих плодов, взятых по два, можно получить? Сколько таких наборов получится, если: 1) плоды в наборе не повторяются; 2) можно брать по два одинаковых плода?
1) Получатся наборы: БА («банан, ананас» и «ананас, банан» – один и тот же набор), АР и РБ.
.
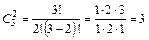2) Получатся наборы: ББ, БА, БР, АА, АР, РР.
.
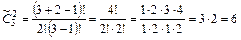Задачи
1. В ящике 15 белых, 12 красных и 14 синих шаров. Вынули один шар. Определить вероятность того, что вынутый шар красный.
2. В денежно-вещевой лотерее на серию из 1000 билетов приходится 3 денежных и 8 вещевых выигрышей. Какова вероятность какого-либо выигрыша на один лотерейный билет?
3. Бросается один раз игральная кость. Какова вероятность того, что выпадет 1 или 5 очков?
4. В ящике 8 белых и 4 синих шара. Вынули сразу 2 шара. Определить вероятность того, что все шары синие?
5. В коробке 20 ламп - 18 исправных и 2 бракованных. Из коробки вынимают 3 лампы. Какова вероятность того, что все они исправные?
6. Бросается один раз игральная кость. Какова вероятность того, что выпадет 1 или 5 очков?
7. Сколько различных слов можно получить перестановками всех букв в слове ЖУК?
8. Сколько различных слов можно получить перестановками всех букв в слове МАТЕМАТИКА?
9. Сколькими способами из 5 шаров можно выбрать 2?
10. Сколькими способами из 10 студентов можно выбрать 3 делегатов на конференцию?
Свойства вероятности
Дата добавления: 2022-11-11; просмотров: 23; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!