Решение систем методом Зейделя
Тема. Решение систем линейных алгебраических уравнений
1.  Решение систем линейных уравнений методом итераций
Решение систем линейных уравнений методом итераций
Дана система линейных уравнений
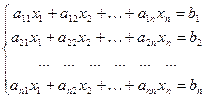 (1)
(1)
Или в матричном виде:
АХ = В (2)
где
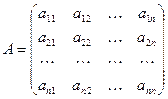 ,
, 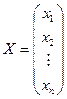 ,
, 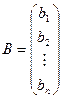 .
.
Пусть диагональные элементы главной матрицы системы 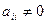 для всех i.
для всех i.
Выразим х1 из первого уравнения системы, х2 - из второго уравнения и т.д. В результате получим систему, эквивалентную системе (1):
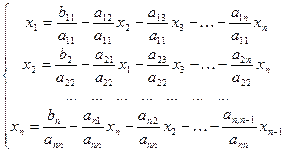 (3)
(3)
Введя обозначения: 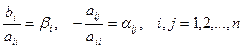 .
.
Тогда система (3) запишется в виде:
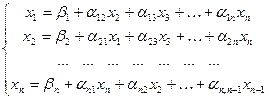 (3′)
(3′)
Система (3′) называется системой, приведенной к нормальному виду, и вводя обозначения:
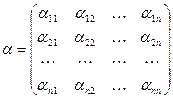
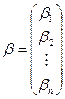 ,
,
Запишем систему (3′) в матричной форме:
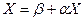
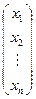 =
= 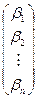 +
+ 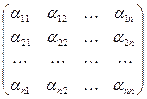 ·
· 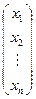 (4)
(4)
Решим систему (4) методом последовательных приближений. За нулевое приближение примем столбец свободных членов:
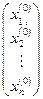 =
= 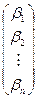 - нулевое приближение, далее строим матрицы - столбцы:
- нулевое приближение, далее строим матрицы - столбцы:
|
|
|
первое приближение: 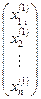 =
= 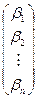 +
+ 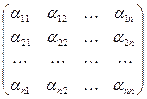 ·
· 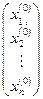 ;
;
второе приближение: 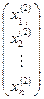 =
= 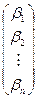 +
+ 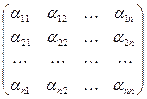 ·
· 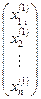 и т.д.
и т.д.
Любое (k + 1 )-е приближение вычисляется по формуле:
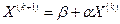 (k = 0, 1, …, n) (5)
(k = 0, 1, …, n) (5)
Если последовательность приближений 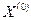 ,
, 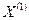 , ….,
, …., 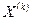 имеет предел, то этот предел является решением системы (3).
имеет предел, то этот предел является решением системы (3).
Условие сходимости итерационного процесса.
Пусть дана приведенная к нормальному виду система линейных уравнений 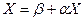 . Итерационный процесс и его сходимость зависят от величины элементов матрица
. Итерационный процесс и его сходимость зависят от величины элементов матрица 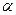 следующим образом: если сумма модулей элементов строк или сумма модулей элементов столбцов меньше единицы, то процесс итерации для данной системы сходится к единственному решению независимо от выбора начального вектора.
следующим образом: если сумма модулей элементов строк или сумма модулей элементов столбцов меньше единицы, то процесс итерации для данной системы сходится к единственному решению независимо от выбора начального вектора.
Следовательно, условие сходимости можно записать так:
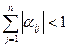 или
или 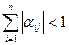
Следствия.
1) Процесс итерации заведомо сходится, если элементы матрицы 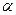 удовлетворяют неравенству
удовлетворяют неравенству 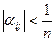 , где n - число неизвестных данной системы.
, где n - число неизвестных данной системы.
2) Сходимость итерационного процесса связана с нормами матрицы 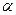 следующими соотношениями:
следующими соотношениями: 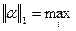
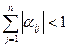 (*)
(*)
либо 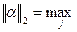
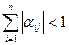 (**)
(**)
|
|
|
либо 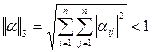 (***)
(***)
то процесс итерации линейной системы сходится к единственному решению.
Оценка погрешности приближенного процесса метода итерации.
Если задана допустимая оценка погрешности ε и Хi - вектор точных значений неизвестных линейной системы, а 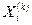 есть k-е приближение значений неизвестных, вычисленное методом итерации, то для оценки погрешности
есть k-е приближение значений неизвестных, вычисленное методом итерации, то для оценки погрешности 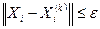 метода применяется формула:
метода применяется формула:
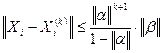 (6)
(6)
где 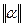 - одна из трех норм матрицы
- одна из трех норм матрицы 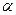 ,
, 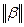 - та же норма вектора β, а k - число итераций, необходимое для достижения заданной точности. При этом предполагается, что последовательные приближения
- та же норма вектора β, а k - число итераций, необходимое для достижения заданной точности. При этом предполагается, что последовательные приближения 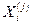 вычисляются точно, в них отсутствуют погрешности округления.
вычисляются точно, в них отсутствуют погрешности округления.
Т.е. 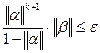 ,
, 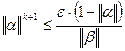 , логарифмируя, определим k.
, логарифмируя, определим k.
Пример.
Дана система уравнений 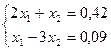
1) Записать систему в матричном виде и решить: а) методом Крамера;
б) методом Гаусса;
2) Привести систему к нормальному виду, записать ее в матричном виде и решить методом итераций, с точностью ε = 10-3.
|
|
|
Решение.
1) Ведем матрицы А = 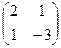 ;
; 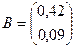 ;
; 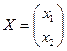 , тогда система в матричном виде А·Х = В.
, тогда система в матричном виде А·Х = В.
а) Метод Крамера. Главный определитель системы: 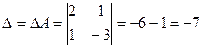 ; дополнительные определители системы:
; дополнительные определители системы: 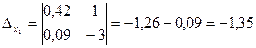
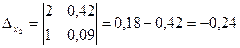 .
.
Т.о. 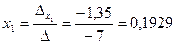 ;
; 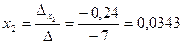 .
.
б) Метод Гаусса. Расширенная матрица системы: 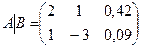 Х
Х 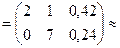
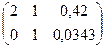
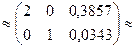
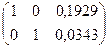 ;
;
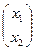 =
= 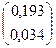
2) Приведем систему к нормальному виду, т.е выразим х1 и х2 соответственно из первого и второго уравнений:
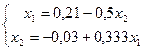 или
или 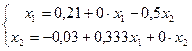
Введем матрицы 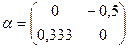 ,
, 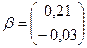 ,
, 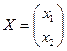
Вычислим нормы матрицы 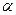 :
:
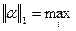
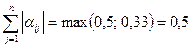 < 1 (суммы по строке)
< 1 (суммы по строке)
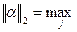
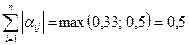 < 1 (сумма по столбцам)
< 1 (сумма по столбцам)
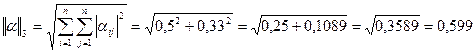 < 1
< 1
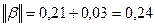
Используя норму 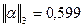 по формуле (6)
по формуле (6)
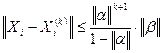 =
= 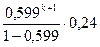 =
= 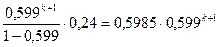
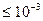
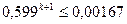 логарифмируем
логарифмируем 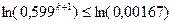
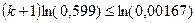 ;
; 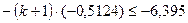 ;
; 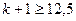 ;
; 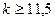
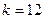 , но как правило, теоретическая оценка числа итераций, необходимых для обеспечения заданной точности, практически оказывается завышенной.
, но как правило, теоретическая оценка числа итераций, необходимых для обеспечения заданной точности, практически оказывается завышенной.
В качестве нулевого приближения примем столбец свободных членов:
Х(0) = 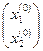 =
= 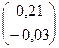
Первое приближение:
Х(1) = 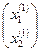 =
= 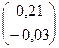 +
+ 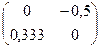 ·
· 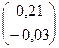 =
= 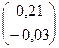 +
+ 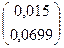 =
= 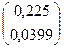
Второе приближение:
Х(2) = 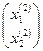 =
= 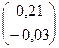 +
+ 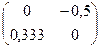 ·
· 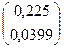 =
= 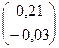 +
+ 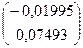 =
= 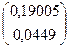
Третье приближение:
Х(3) = 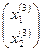 =
= 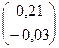 +
+ 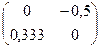 ·
· 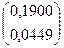 =
= 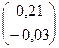 +
+ 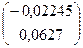 =
= 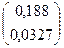
Четвертое приближение:
Х(4) = 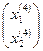 =
= 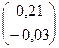 +
+ 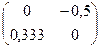 ·
· 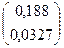 =
= 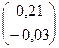 +
+ 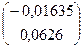 =
= 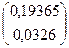
Пятое приближение:
Х(5) = 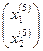 =
= 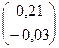 +
+ 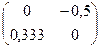 ·
· 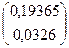 =
= 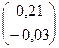 +
+ 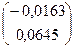 =
= 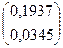
Шестое приближение:
Х(6) = 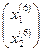 =
= 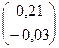 +
+ 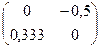 ·
· 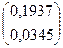 =
= 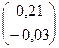 +
+ 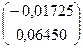 =
= 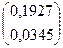
Таким образом, приближенное решение:
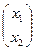 =
= 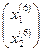 =
= 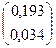
Решение систем методом Зейделя
|
|
|
Модификация метода последовательных приближений: при вычислении 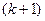 -го приближения неизвестного хi учитывается уже найденное ранее
-го приближения неизвестного хi учитывается уже найденное ранее 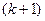 -е приближение неизвестных x1, x2, …, xi-1.
-е приближение неизвестных x1, x2, …, xi-1.
Пусть система имеет нормальный вид (3′):
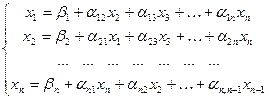
Выбираем произвольно начальное приближение корней: 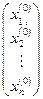 и подставляем в первое приближение:
и подставляем в первое приближение:
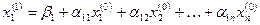
Полученное первое приближение 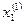 подставляем во второе уравнение системы:
подставляем во второе уравнение системы:
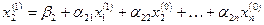
Полученные первые приближения 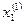 и
и 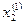 подставляем в третье уравнение системы:
подставляем в третье уравнение системы:
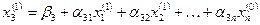
и т.д. Наконец:
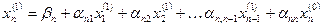 .
.
Аналогично строим вторые, третьи и т.д. итерации.
Пример.
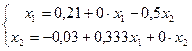
За нулевое приближение примем соответствующие значения свободных членов:
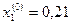 ;
; 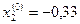
Строим итерации по методу Зейделя:
Первое приближение (при определении х2 используем х1 из предыдущего уравнения):
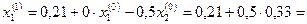 0,375
0,375
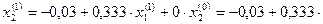 0,375 = 0,094
0,375 = 0,094
Второе приближение
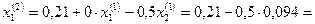 0,163
0,163
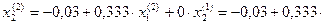 0,163 = 0,024
0,163 = 0,024
Третье приближение:
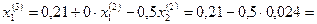 0,198
0,198
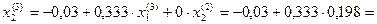 0,035
0,035
Четвертое приближение:
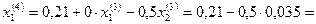 0,1925
0,1925
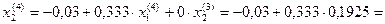 0,034.
0,034.
Таким образом, уже четвертое приближение дает требуемую точность:
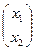 =
= 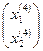 =
= 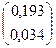 .
.
Дата добавления: 2022-11-11; просмотров: 22; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
