Задание на дом. Домашняя работа.
Тема «Первообразная. Интегралы».
Повторение. Первообразная
Функцию, восстанавливаемую по заданной ее производной или дифференциалу, называют первообразной.
Дифференцируемая функция 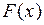 называется первообразной для функции
называется первообразной для функции 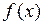 на заданном промежутке, если для всех х из этого промежутка справедливо равенство
на заданном промежутке, если для всех х из этого промежутка справедливо равенство 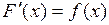 .
.
Из этого определения вытекает, что всякая функция по отношению к своей производной является первообразной.
Так, функция 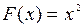 есть первообразная функции
есть первообразная функции 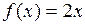 на интервале
на интервале 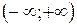 , поскольку для всех
, поскольку для всех 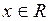 имеет место равенство
имеет место равенство 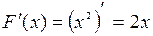 .
.
1. Найти первообразную функции 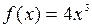 .
Решение: Используя правило дифференцирования, можно догадаться, что на интервале .
Решение: Используя правило дифференцирования, можно догадаться, что на интервале 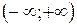 первообразной является первообразной является 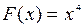 . Действительно, . Действительно, 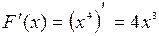 для всех для всех 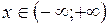 .
2. Найти первообразную функции .
2. Найти первообразную функции 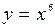 на множестве R.
Решение: Степень на множестве R.
Решение: Степень 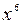 получается при дифференцировании получается при дифференцировании 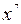 . Так как . Так как 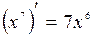 , то, чтобы при дифференцировании , то, чтобы при дифференцировании 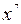 получить перед получить перед 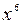 коэффициент 1, нужно коэффициент 1, нужно 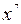 взять с коэффициентом 1/7. Следовательно, взять с коэффициентом 1/7. Следовательно, 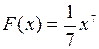 . .
|
Новый материал.
Неопределенный интеграл
Как уже было отмечено, первообразную можно находить не только по данной ее производной, но и по ее дифференциалу. В дальнейшее мы будем этим пользоваться.
Определение. Совокупность всех первообразных 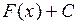 функции
функции 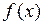 на рассматриваемом промежутке называется неопределенным интегралом и обозначается символом
на рассматриваемом промежутке называется неопределенным интегралом и обозначается символом 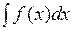 , где
, где 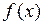 - подынтегральная функция,
- подынтегральная функция, 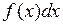 - подынтегральное выражение, х – переменная интегрирования.
- подынтегральное выражение, х – переменная интегрирования.
|
|
|
Таким образом, если 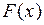 - какая-нибудь первообразная функции
- какая-нибудь первообразная функции 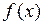 на некотором промежутке, то
на некотором промежутке, то 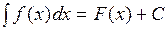 , где С – любое действительное число.
, где С – любое действительное число.
Замечание. Наличие постоянной С делает задачу нахождения функции по ее производной не вполне определенной; отсюда происходит название «Неопределенный интеграл».
Так, пользуясь определением неопределенного интеграла, можно записать: 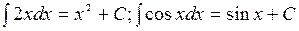 .
.
Значит, чтобы найти неопределенный интеграл от заданной функции, нужно найти какую-нибудь одну из ее первообразных и прибавить к ней произвольную постоянную С.
1.Найти неопределенный интеграл 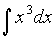 .
.
Решение: 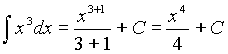
2. Найти интеграл 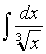 .
.
Решение: 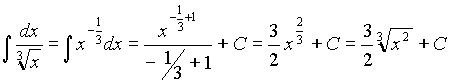
Определенным интегралом 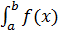 в пределах от а до в от функции f ( x ), непрерывной на отрезке [а, в], называется приращение любой ее первообразной F(x) при изменении аргумента х от значения х=а до х=в:
в пределах от а до в от функции f ( x ), непрерывной на отрезке [а, в], называется приращение любой ее первообразной F(x) при изменении аргумента х от значения х=а до х=в:
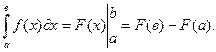
Данная формула так же называется формулой Ньютона-Лейбница, ее называют основной формулой интегрального исчисления.
Свойства определенного интеграла.
- Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определенных интегралов от слагаемых функций:
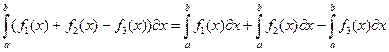
- Постоянный множитель можно выносить за знак определенного интеграла:
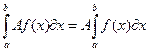
- При перестановке пределов интегрирования определенный интеграл меняет свой знак на противоположный:
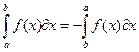
- Определенный интеграл с одинаковыми пределами равен нулю:
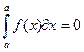
- Отрезок интегрирования можно разбивать на части:
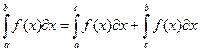
6. ПРИМЕРЫ: Вычислить интеграл:
|
|
|
1) 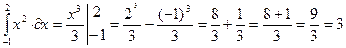 ;
;
2) 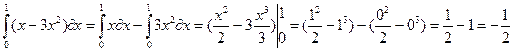 ;
;
3) 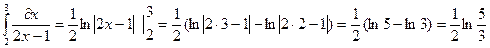 ;
;
4) 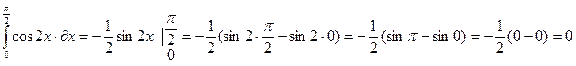 .
.
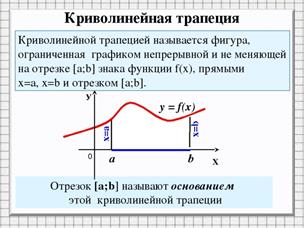
- Геометрический смысл определенного интеграла
8. 
9. 
10. 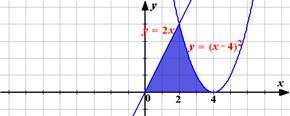
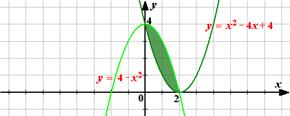
Именно в нахождении площади криволинейной трапеции заключается геометрический смысл определенного интеграла.
Рассмотрим несколько способов вычисления площади определенного интеграла.
Для более удобного и точного вычисления площади фигуры воспользуемся координатной плоскостью. Существует несколько способов расположения фигуры относительно оси Х.
Первый способ (записываем в тетрадь).
1. Строим координатную плоскость
2. Проводим кривую выше оси х и обозначим ее функцией у=f(х).
3. Проведем прямые х=а и х=b параллельные оси у и пересекающие функцию у= f(х). и прямую у=0.
4. А теперь обведем кривую и ниже прямую заключенную между прямыми х=а и х=б, прямые между кривой и прямой у=0
Итак, мы должны найти площадь данной фигуры, которая мы уже знаем называется криволинейной трапецией.
|
|
|
Для нахождения площади данной фигуры используется формула, вы ее уже знаете как формулу Ньютона – Лейбница.
b b
S=∫f(x)dx=F(x)|=F(b)-F(a)
a a
А теперь давайте рассмотрим пример на нахождение площади криволинейной трапеции.
Дано: х-у+2=0, у=0, х=-1, х=2. Из уравнения кривой выразим у через х (так как мы знаем что у-зависимая переменная, а х – независимая)
у=х+2 – линейная функция, построим график данной функции, достаточно две пары чисел чтобы построить график данной функции.
х=0, у=2 х=1, у=3.
Строим прямую на координатной плоскости. Проводим прямые ограничивающие данную кривую. Обведем получившиеся отрезки ограниченные данными линиями. У нас получилась трапеция. Найдем площадь данной фигуры.
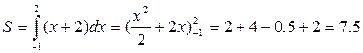
Итак, с помощью формулы Ньютона- Лейбница мы нашли площадь криволинейной трапеции. Существует несколько способов нахождения площади криволинейной трапеции. Рассмотрим второй способ.
Второй способ :( записываем в тетрадь)
Второй способ заключается в том, что площадь криволинейной трапеции мы с вами рассмотрим ниже оси х.
1. Строим координатную плоскость
|
|
|
2. Проводим кривую под осью х и обозначим ее функцией у=f(х).
3. Проведем прямые х=а и х=в параллельные оси у и пересекающие функцию у= f(х). и прямую у=0.
4. А теперь обведите прямые заключенные между точками пересечения прямых и кривой и заштрихуем ту часть плоскости которая находится внутри данных прямых.
У нас получилось, что фигура находиться ниже оси у, показывает значения у в 4 четверти (минус).
Площадь данной криволинейной трапеции тоже вычисляется по формуле Ньютона- Лейбница. В данном случае площадь криволинейной трапеции может получиться отрицательным числом. Чтобы площадь не принимала отрицательного значения, необходимо использовать математический символ. Какой? Модуль. b b
S=|∫f(x)dx|= |F(x)| |=|F(b)-F(a)| a
А теперь давайте рассмотрим пример на нахождение площади криволинейной трапеции находящейся в 4 четверти.
Пример: у=-3х, у=0, х=2
Функция, которая здесь рассматривается называется прямой пропорциональностью и проходит чрез начало координат, для ее построения достаточно одну пару точек.
х=1, у=-3 строим данные прямые на плоскости. Так как полученная фигура находится в четверти, то ее площадь вычисляется по второй формуле.
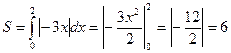
Задание на дом. Домашняя работа.
Вычислите интегралы:
1. 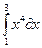 2.
2. 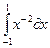 3.
3. 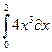 4.
4. 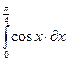 5.
5. 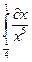
2. Найти площади фигур, ограниченных указанными линиями
а) x+2y-4-0, y-0, x—3, x=2.
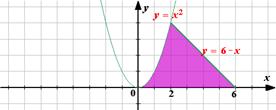
b) y=x2, y=0, x=2, x=3.
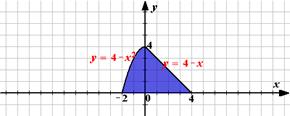
c) y=-x2+4, y=0
Дата добавления: 2022-07-16; просмотров: 17; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
