Вычисление невязки во второй группе.

Тамбовский филиал

федерального государственного бюджетного образовательного

учреждения высшего образования

«Мичуринский государственный аграрный университет»

Кафедра: Ландшафтная архитектура, землеустройства и кадастры.

Шифр 181656

Контрольная работа.

По дисциплине: Теория математической обработки геодезических измерений.

На тему: №6,№16,№26.

ФИО: Голованов Г.В.

Выполнил: студент 3 курса, ФЗБ31 группы

Направление подготовки: 21.03.02 «Землеустройство и кадастры»

Проверил преподаватель: Щукин Р.А. /

Тамбов 2020.

Содержание.

1. Введение.

2. В чем принципиальное различие формул Гаусса и Бесселя, применяемых для оценки точности однородных измерений.

3. Формула Бесселя.

4. Вычисление невязки во второй группе.

5. Заключение.

6. Список используемой литературы.

Введение.

Геодезические измерения определяют относительное положение точек земной поверхности.

Различают следующие виды измерений:

1) линейные – получают наклонные и горизонтальные расстояния между точками. Инструменты: мерные ленты, рулетки, проволоки, оптические свето- и радиодальномеры;

2) угловые – определяют величины горизонтальных и вертикальных углов. Инструменты: эклиметры, буссоли, теодолиты;

3) высотные – получают разности высот отдельных точек. Инструменты: баронивелиры, теодолиты-тахеометры, нивелиры.

Измерения бывают:

1) непосредственные (прямые);

2) косвенные.

Измерения бывают:

1) равноточные (один объект наблюдения, один наблюдатель, один мерный прибор, одна методика наблюдений, одинаковые условия внешней среды);

2) неравноточные (когда не соблюдаются выше перечисленные условия).

Измерения сопровождаются погрешностями (ошибками): грубыми (из-за невнимательности наблюдателя), систематическими (из-за несовершенства приборов) и случайными (зависящими от многих причин и неподдающимися никаким прогнозам).

Грубые погрешности исключают повторными наблюдениями. Систематические погрешности можно учесть, вводя поправки в измеренные величины за длину ленты, длину метра реек, за погрешности прибора и т.д. Случайные погрешности исключить нельзя, но можно ослабить их влияние на измеренные величины путем многократных наблюдений.

В чем принципиальное различие формул Гаусса и Бесселя, применяемых для оценки точности однородных измерений.

Оценить точность каких-либо измерений - это значит определить на основе полученных результатов сравнимые числовые (количественные) характеристики, выражающие качественную сторону самих измерений и условий их проведения. Количественные характеристики измерений или критерии оценки точности измерений устанавливаются теорией вероятности и теорией ошибок (в частности, способом наименьших квадратов). Согласно этим теориям оценка точности результатов измерений производится только по случайным ошибкам.

В теории погрешностей точность измерений характеризуется средней квадратической погрешностью, которая была введена знаменитым немецким математиком и геодезистом К. Ф. Гауссом (1777–1855 гг.) и обозначается через m:

m = ± √ (Δ₁² + Δ₂² + .. + Δ_n²) / n = ± √ [Δ²] / n, (4.5)

где Δ₁, Δ₂, …, Δ_n – случайные погрешности;

n – число измерений.

Средняя квадратическая погрешность является надежным критерием для оценки точности измерений. Она даже при небольшом числе измерений достаточно устойчива и хорошо отражает наличие крупных случайных ошибок, которые по существу и определяют качество измерений.

Формула (4.5) применена для вычисления средней квадратической погрешности, когда известно истинное значение измеряемой величины. Эти случаи в практике весьма редки. Как правило, истинное значение измеряемой величины неизвестно, но из измерений можно получить наиболее надежный результат – арифметическую середину. Получим формулу для вычисления средней квадратической погрешности при помощи уклонения отдельных результатов от арифметической середины по так называемым вероятнейшим погрешностям V.

Пусть l₁, l₂, …, l_n – результаты равноточных измерений одной и той же величины, истинное значение которой Х, а арифметическая середина – L. Тогда можно вычислить n случайных или истинных погрешностей

Δ_i = l_i – X (4.6)

и n вероятнейших погрешностей

V_i = l_i – L. (4.7)

Сумма n равенству (4.7)

[V] = [l] – nL. (4.8)

Но, согласно равенству (4.4) nL = [l], поэтому

[V] = 0, (4.9)

т. е. сумма вероятнейших погрешностей всегда должна быть равна нулю.

Вычитая из равенства (4.6) равенство (4.7), получим

Δ_i – V_i = L – X. (4.10)

В правой части равенству (4.10) мы имеем случайную погрешность арифметической середины. Обозначим ее через ε. Тогда

Δi = V_i + ε. (4.11)

Возведем в квадрат равенство (4.11), возьмем их сумму и разделим ее на n:

[Δ²] / n = [V²] / n + nε² / n + 2ε[V] / n. (4.12)

Левая часть этого равенства есть не что иное как m². Последнее слагаемое правой части ввиду равенства (4.9) равно нулю.

m² = [V²] / n + ε². (4.13)

Случайную погрешность ε заменим ее средним значением, т. е. средней квадратической погрешностью арифметической середины. Ниже будет доказано, что средняя квадратическая погрешность арифметической середины

М ² = ε ² = m ²/ n. (4.14)

Тогда

m ² – m² / n = [V ²] / n или m ²(n – 1) / n = [V ²] / n,

откуда

m ² = [V ²] / (n – 1), или m = √ [V ²] / (n – 1). (4.15)

Формула (4.15) называется формулой Бесселя и имеет большое практическое значение. Она позволяет вычислять среднюю квадратическую погрешность по вероятнейшим уклонениям результатов измерений от арифметической средины.

Кроме средней квадратической погрешности различают еще среднюю, вероятную и относительную погрешности.

Средней погрешностью (Θ) называют среднее арифметическое из абсолютных значений случайных погрешностей т. е.

Θ = (|Δ₁| + |Δ₂| + … + |Δ_n| ) / n = [|Δ|] / n. (4.16)

В теории погрешности доказывается, что при n → ∞ Θ = 0,8 m, или m = 1,25Θ.

Иногда в прикладных вопросах пользуются вероятной погрешностью r. Вероятной погрешностью называют такое значение случайной погрешности в одном ряду равноточных измерений, по отношению к которой одинаково возможна погрешность как больше, так и меньше этого значения, по абсолютной величине. Для нахождения r все погрешности данного ряда располагают в порядке возрастания по абсолютной величине и выбирают то значение, которое занимает среднее положение, т. е. погрешностей меньше его столько же, сколько и больше. Вероятная погрешность связана со средней квадратической погрешностью соотношением r = 2/3 m = 0,67 m или m = 1,5 r.

Как видно, m > Θ и m > r, что показывает, что средняя квадратическая погрешность лучше характеризует точность измерений, чем средняя и вероятная погрешности.

Оценку точности таких измеренных величин, как линии, площади и объемы часто производят с помощью относительной погрешности. Относительной погрешностью называют отношение абсолютной погрешности к значению измеренной величины. Относительная погрешность записывается в виде дроби, в числителе которой стоит единица, а в знаменателе – число, показывающее какую долю измеряемой величины должна составлять допустимая погрешность. Например, длина стороны D = 150 м измерена с абсолютной погрешностью m_d = 0,05 м. Тогда относительная погрешность результата измерения составит m_d / D = 0,05 м / 150 м = 1 / 3000.

Величина 1 / 3000 означает, что на 3000 м расстояния может быть допущена погрешность в 1 м. Чем больше знаменатель относительной погрешности, тем выше точность измерений. Точность всех линейных измерений в геодезии всегда задается относительной погрешностью, которая приводится в соответствующих инструкциях и наставлениях по производству данного вида геодезических работ.

Формула Бесселя.

m ² = [V ²] / (n – 1), или m = √ [V ²] / (n – 1).

Эта формула называется формулой Бесселя и имеет большое практическое значение. Она позволяет вычислять среднюю квадратическую погрешность по вероятнейшим уклонениям результатов измерений от арифметической средины.

Кроме средней квадратической погрешности различают еще среднюю, вероятную и относительную погрешности.

Средней погрешностью (Θ) называют среднее арифметическое из абсолютных значений случайных погрешностей т. е.

Θ = (|Δ₁| + |Δ₂| + … + |Δ_n| ) / n = [|Δ|] / n. (4.16)

В теории погрешности доказывается, что при n → ∞ Θ = 0,8 m, или m = 1,25Θ.

Вычисление невязки во второй группе.

Для вычисления невязки будем использовать функцию с двумя аргументами 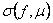, где 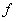- некоторое выражение (формула), 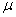- желаемое значение. Ниже даны выражения вычисления функций невязки для множества операторов. С помощью этих функций рекурсивно можно вычислять невязку произвольного выражения, использующего эти операторы.

Чтобы отличать формулы от вычисляемых значений, будем через 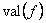обозначать вычисленное значения выражения 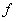при заданных значениях переменных, входящих в 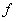. Еще потребуется обозначение 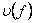- это количество переменных в выражении 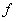. Задача формулируется в виде системы ограничений над переменными. Ограничение – это булево выражение, значение которого должно быть истинным. (Будем использовать 1 для истинного выражения и 0 для ложного). Таким образом, рекурсивное вычисление начинается с , где 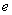- это ограничение. Если для оператора указано выражение для вычисления 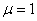, это значит что это глобальное ограничение, то есть оператор не может быть вложен в другие операторы или участвовать в выражение как его элемент. К таким операторам относятся операторы оптимизации и функциональные операторы.Если вычисленное и желаемое значение совпадают, либо в выражении нет переменных, то невязка равна нулю:

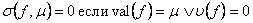
Если некоторое булево выражение напрямую использовано в арифметическом выражении и желаемое значение отлично от нуля и единицы, то вычислении производятся следующим образом:

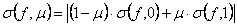
В качестве невязки используется оценка, на сколько минимально нужно изменить значение переменной, чтобы противоречивое ограничение стало бы истинным. Часто для «взвешивания» невязок нескольких переменных в одном выражении используется формула:

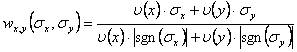
Для линейного ограничения использование такого взвешивания даст невязку как «среднее значение, на которое нужно изменить одну из переменных, чтобы ограничение стало бы истинным».

Невязка проектировалась таким образом, чтобы быть максимально инвариантной к форме записи, оставаясь при этом простой для вычисления для произвольных выражений.

Пример 1: линейное выражение.

Пусть для выражения 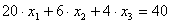невязка имеет значение 0.933. Если пользоваться классической невязкой для равенства 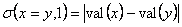, то для выражения 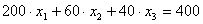невязка будет 9.33, то есть в 10 раз больше, хотя мы имеем тождественное выражение и невязка должна бы быть той же самой. В предлагаемом варианте вычисления невязки в обоих случаях будет одинаковой.

Пример 2: суммы с условиями.

Иногда условия могут находиться не непосредственно в корне ограничения, а быть вложенными внутрь выражения. Так, уравнение

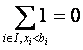
эквивалентно множеству ограничений 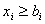. Для классической формы вычисления невязка всегда будет 0 или 1. В предлагаемом варианте вычисления значения невязки для обоих случаев будут одинаковы.

Для некоторых выражений невязка не существует. Например, при использовании вещественной переменной 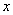для выражения 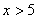теоретически невязку точно вычислить невозможно. Так при 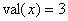невязка будет числом, «бесконечно близким» к 2, но большим 2. Для таких случаев будем использовать малое число 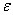, отражающее используемую для ограничений точность. В этом случае невязка будет равно 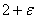. Если мы имеет дело с целочисленными выражениями, то имеет смысл положить для них .

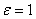Заключение.

Любая геодезическая сеть, с теоретической точки зрения, представляет собой систему, объединяющую все измеренные элементы. Из теории вероятностей известно, что при анализе систем необходимо учитывать все связи между ее отдельными элементами, т. е. в данном случае– связи между измеренными величинами.

Математическая обработка систем геодезических измерений выполняется в два этапа. На первом этапе производится математическая обработка рядов многократных измерений всех величин по отдельности. В результате для каждого измеряемого элемента получают окончательный результат (оценку математического ожидания) с некоторой точностью. На этом этапе обработки не учитываются связи между измеряемыми величинами. Целью является получение для каждого измеряемого элемента наиболее надежного значения (по возможности неискаженного грубыми и систематическими ошибками) и его точности – средней квадратической ошибки.

На втором этапе в качестве непосредственных измерений выступают окончательные результаты математической обработки первого этапа, и выполняется их дальнейшая математическая обработка уже с учетом всех связей между ними.

Таким образом можно сделать вывод о том, что особенностью математической обработка геодезических измерений являются основополагающие знания студента в высшей математике, которые применяются как на практике, так и в теории.

Список используемой литературы.

1. Корнеев В.И. УМКД«Теория математической обработки геодезических

измерений»

2. Большаков В.Д. Теория математической обработки геодезических

измерений / В.Д.Большаков, П.А. Гайдаев. – 2-е изд., перераб. и доп. – М.:

Недра, 2017. – 367 с.

3. Большаков В.Д. Практикум по теории математической обработки

геодезических измерений: Учеб. пособие для вузов / В.Д. Большаков, Ю.И.

Маркузе. – М.: Недра, 2014. – 352 с.

4. Голубев В.В. Основы теории ошибок: Учебное пособие / В.В. Голубев. –

М.: МИИГАиК, 2015. – 66 с.

5. Дегтярев А.М. Теория математической обработки геодезических

измерений. Вероятностно-статистические методы: Конспект лекций для

студентов геодезического факультета / А.М. Дегтярев. – Новополоцк: ПГУ,

2005. – 212 с

6. Ю.П. Боглаев. Вычислительная математика и программирование. М.:

Высшая школа. 2010.

7. Е.А. Волков. Численные методы. М.: Наука. 2017.

8. А.А. Амосов, Ю.А. Дубинский, Н.В. Копченова. Вычислительные методы

для инженеров. М.: Высшая школа. 2014.

9. И.А. Соловьев. Прикладная математика. Численные методы. Учебное

пособие. М.: Изд-во ГУЗ. 2017.

Дата добавления: 2022-07-02; просмотров: 71; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!