Необходимые сведения о формуле Тейлора

Возникновение дифференциальных уравнений

Задача 1. Тело охладилось за 10 минут со 100º до 60º. Температура окружающего воздуха поддерживается равной 20º. Определить, за сколько минут тело остынет до 25º. Принять, что скорость остывания тела пропорциональна разности температур тела и окружающей среды.

Рис. 4

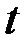Решение. Обозначим через - температуру тела в момент времени (мин.). Тогда имеем 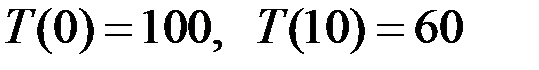. Зависимость температуры тела в момент времени 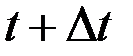от температуры тела в момент времени 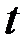(при ничтожно малом значении ) можно выразить уравнением:

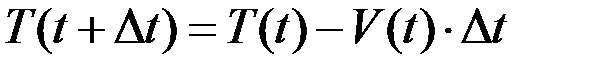, где - скорость остывания тела в момент времени 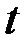. (В силу ничтожности можно считать, что скорость остывания практически не изменяется за интервал времени ). Таким образом, имеем:

Перенеся первое слагаемое справа налево, и поделив все уравнение на , получим: . Перейдем в полученном уравнении к пределу по 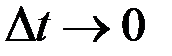: . (6.11)

Найдем коэффициент 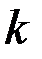с помощью почленного интегрирования уравнения (6.11):

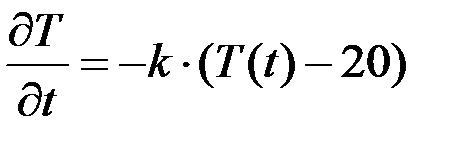
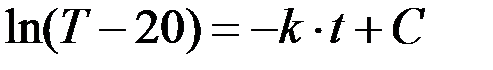
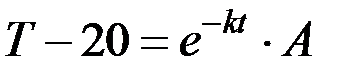
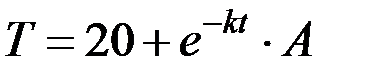
Подставим 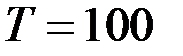в момент времени 0: .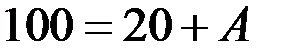

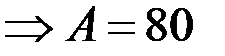Подставим 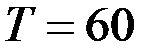в момент времени 10: .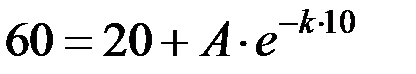

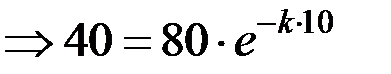
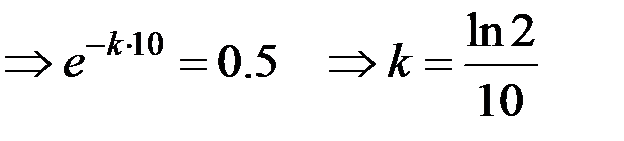Итак, получили 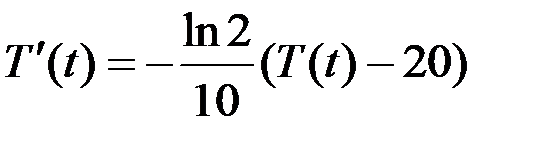при начальном условии .

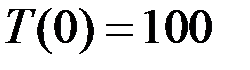Задача 2. В сосуд, содержащий 10 л воды, начинает непрерывно поступать со скоростью 2 л в минуту раствор, в каждом литре которого содержится 0.3 кг соли. Поступающий в сосуд раствор перемешивается с водой, и смесь вытекает из сосуда с той же скоростью. Сколько соли будет в сосуде через 5 минут?

Решение. Примем предположение, что поступающий в сосуд солевой раствор равномерно перемешивается с содержащейся в сосуде жидкостью.

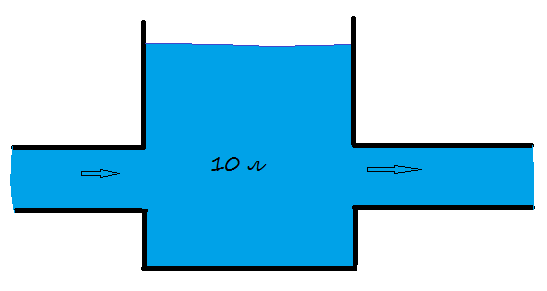
Рис. 2

Обозначим 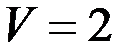л/мин. – скорость поступления солевого раствора в сосуд, С = 0.3 кг/л – концентрация поступающего солевого раствора. Тогда количество соли, поступающее в сосуд за ничтожно малое время 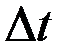минут будет равно .

Пусть 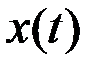– количество соли (кг) в сосуде в момент времени 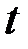. Тогда в момент времени 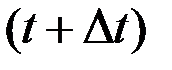количество соли будет равно:

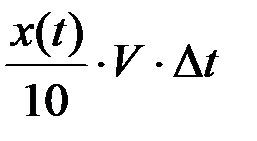, где слагаемое есть количество соли, вытекающее из сосуда за время 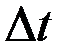. Итак, имеем:

. Преобразуем это уравнение, перенеся первое слагаемое справа налево и поделив все уравнение на :

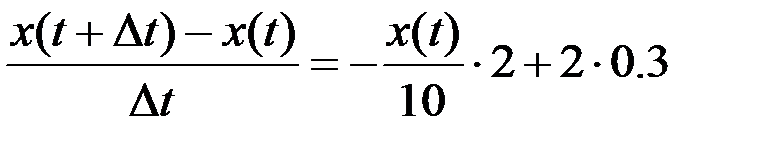. Теперь, взяв предел выражения при 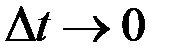, получим:

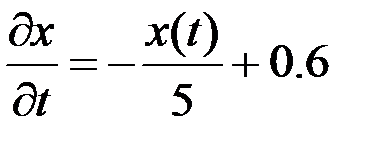. При этом 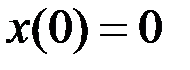(в начальный момент времени в сосуде была чистая вода). Для ответа на вопрос задачи надо произвести интегрирование уравнения по частям и найти значение свободной константы С с помощью начального условия.

Задача 3. Дно резервуара, вместимость которого 300 л, покрыто солью. Допуская, что скорость растворения соли пропорциональна разности между концентрацией насыщенного раствора (1 кг соли на 3 л воды) и концентрацией в данный момент, и что данное количество чистой воды растворяет 1/3 кг соли в минуту, найти, сколько соли будет содержать раствор по истечении 1 часа.

Рис. 3

Решение. Концентрация насыщенного раствора соли равна 1 кг соли на 3 л воды, следовательно, считая, что приближенно 1 кг соли занимает объем 1 л, концентрация насыщенного раствора равна .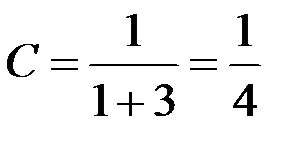

Пусть 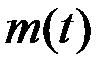– масса соли в резервуаре в момент времени 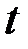, а 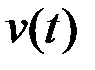– скорость растворения соли в момент времени 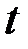. И пусть – ничтожно малый

интервал времени, так что можно считать, что скорость растворения соли в момент времен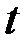и и 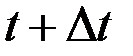примерно одинакова, т.е. . Тогда

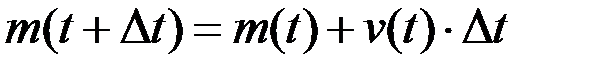По условию .

Найдем коэффициент 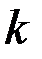из условия, по которому чистая вода растворяет 1/3 кг соли в минуту: .

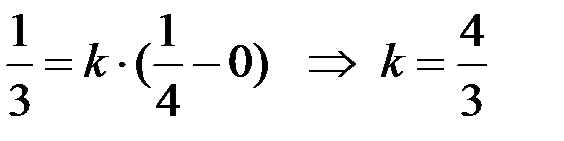Тогда имеем: 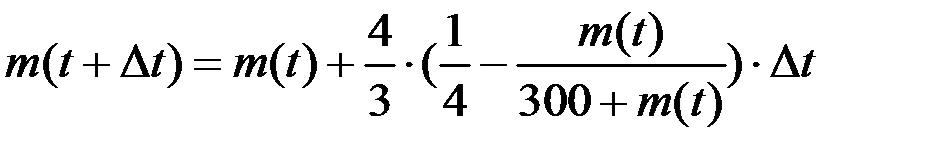. Преобразуем уравнение, перенеся слагаемое 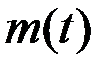налево и поделив все уравнение на 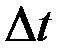: . И перейдя к пределу по 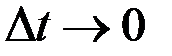получим: 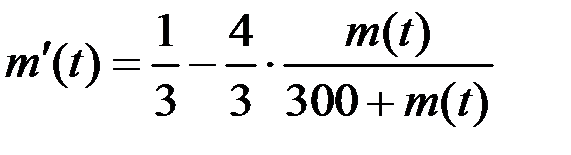, при этом 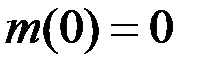, т.к. вначале резервуар содержал чистую воду.

Задача 4. В дне цилиндрического сосуда, наполненного водой и имеющего высоту Н м и радиус основания R м, сделано небольшое отверстие площади 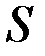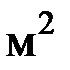(см. рис.). За какой промежуток времени через отверстие вытечет вся вода, если треть воды вытекает за промежуток времени 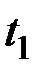секунд?

Решение. Если бы истечение воды происходило равномерно, то решить задачу не представляло бы никаких затруднений — вся вода вытечет за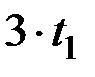

Рис.1

секунд. Но наблюдения показывают, что сначала вода вытекает быстро, а по мере снижения уровня воды в сосуде скорость ее истечения уменьшается. Поэтому надо учесть зависимость между скоростью истечения ( ) и высотой 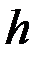(м) столба жидкости над отверстием. Проведенные итальянским физиком Торричелли эксперименты показали, что скорость приближенно выражается формулой , где 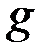— ускорение свободного падения и 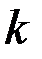— «безразмерный» коэффициент, зависящий от вязкости жидкости и формы отверстия (например, для воды в случае круглого отверстия =0.6).

Сделаем «мгновенный снимок» процесса истечения за ничтожно малый промежуток времени 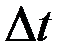. Пусть в начале этого промежутка высота жидкости над отверстием равнялась , а в конце его она понизилась и стала 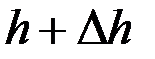, где 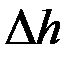- «падение» высоты ( 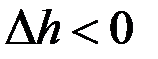). Тогда объем жидкости, вытекшей из сосуда, равен объему цилиндра высотой 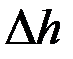и площадью основания , т.е. .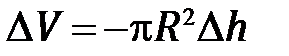

Эта жидкость вылилась в виде цилиндрической струйки, имеющей площадь основания S. Ее высота равна пути, пройденному вытекающей из сосуда жидкостью за промежуток времени 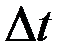. В начале этого промежутка времени скорость истечения равнялась по закону Торричелли , а в конце его она равнялась .

Если 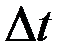весьма мало, то 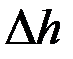тоже очень мало, потому полученные выражения для скорости почти одинаковы. Таким образом, путь, пройденный жидкостью за промежуток времени 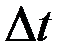, выражается формулой . Значит, объем вылившейся за промежуток времени 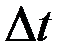жидкости вычисляется по формуле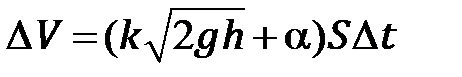

Мы получили два выражения для объема жидкости, вылившейся из сосуда за промежуток времени 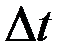. Приравнивая эти выражения, получаем уравнение

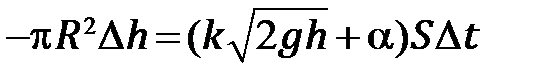(6.6)

Выражение для α неизвестно, чтобы избавиться от α разделим обе части уравнения (6.6) на 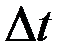и перейдем к пределу при . Поскольку, 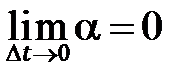, а получаем дифференциальное уравнение

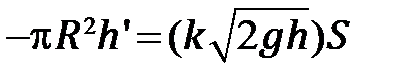(6.7)

Можно рассуждать иначе. Если исследовать процесс в течение «бесконечно малого промежутка времени 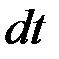и считать, что за промежуток времени не изменяется скорость истечения жидкости из сосуда, вместо приближенного уравнения (6.6) можно получить точное уравнение

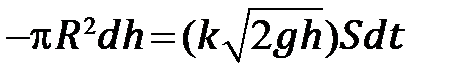, (6.8)

то есть уравнения (6.7) в дифференциальной форме.

Чтобы решить получившееся уравнение, произведем разделение переменных 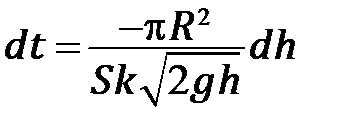. Интегрируя обе части этого уравнения, получим ответ в виде

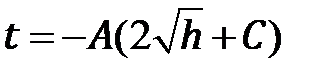(6.9)

где - константа, которая зависит от размеров и формы отверстия, вязкости жидкости и других физических параметров, а постоянная С возникла в ходе решения задачи. Их значения нам неизвестны, но их можно найти, учитывая неиспользованные еще условия задачи.

Сначала найдем значение С. Для этого используем начальные условия. По условию задачи в начале истечения сосуд был наполнен, т. е. высота столба жидкости равнялась H. Иными словами, при имеем 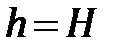. Подставляя в формулу (6.9) значения получаем: 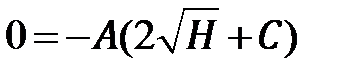и потому 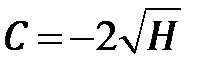. Поэтому равенство (6.9) можно переписать в виде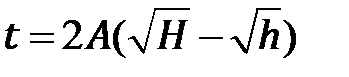

Чтобы найти значение А, вспомним, что за первые 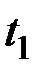мин вытекла треть всей жидкости. Этому соответствует понижение уровня жидкости на 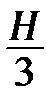. Иными словами, при 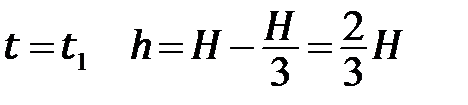. Отсюда находим, что

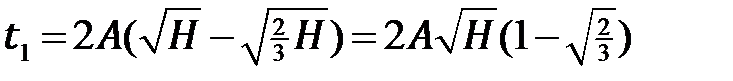
И потому

(6.10)

Теперь уже легко найти время опорожнения сосуда: нам надо найти такое значение 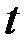, при котором :

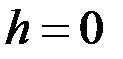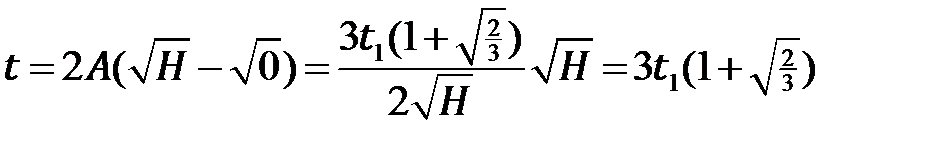
Полученное значение в 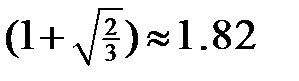раз больше значения 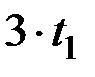, которое получилось в предположении, что жидкость вытекает равномерно.

Разумеется, и это решение не является безукоризненно точным — мы пренебрегли, например, явлениями капиллярности (а они существенны, если диаметр отверстия мал), завихрениями жидкости, так называемым пограничным слоем (слоем жидкости вблизи стенок отверстия, на котором происходит переход значений скорости от нуля до v) и многими иными факторами. Но все же оно точнее, чем решение, основанное на предположении о равномерности истечения жидкости.

Исследуем в заключение полученное решение. Для этого подставим в равенство (6.10) значение , найдем 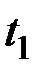и получим, что

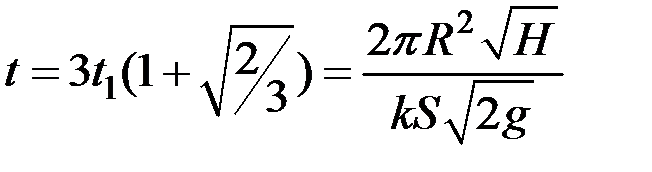
Ясно, что, чем больше значения R и Н (размеры сосуда), тем дольше будет вытекать из него жидкость, как это и следует из полученного ответа. Далее, чем больше площадь отверстия S, тем быстрее вытечет жидкость из сосуда. В том же направлении действует и увеличение ускорения g, а также коэффициента k (чем больше k, тем больше скорость истечения жидкости по формуле Бернулли).

Таким образом, полученная формула выдержала «испытание на здравый смысл». Проведенный контроль подтверждает, что задача решена правильно.

Необходимые сведения о формуле Тейлора

Пусть функция имеет непрерывные производные до порядка 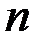включительно в окрестности точки 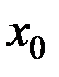. Требуется найти такой многочлен порядка 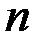, значение которого в точке 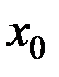, а также значения всех его производных в этой точке до порядка 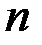включительно совпадают с соответствующими значениями функции . Таким многочленом будет многочлен Тейлора: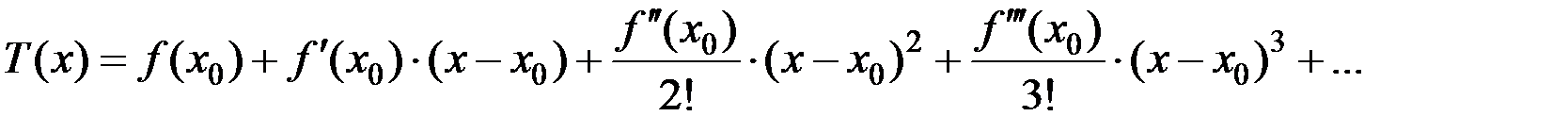

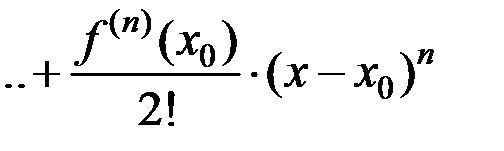
Тогда значение этой функции в точке 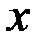близкой к 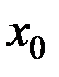можно приближенно вычислять, используя разложение в ряд Тейлора в окрестности точки .

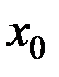То есть .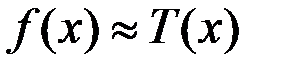

Дата добавления: 2022-07-01; просмотров: 16; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!