Иррациональные уравнения вида «дробь равна нулю».
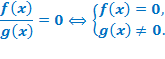
Из этого утверждения вытекают два подхода к решению уравнений такого вида:
· Найти ОДЗ исходного уравнения, решить уравнение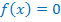 
, проверить корни на принадлежность ОДЗ. Этот случай удобнее использовать в тех случаях, когда найти область допустимых значений проще, чем решить уравнение .
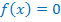· Решить уравнение 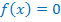и проверить, какие из его корней являются решениями исходного уравнения. Этот случай используется, когда нахождение области допустимых значений затруднительно.
Приведём примеры.
а) 
Найдём область допустимых значений уравнения.
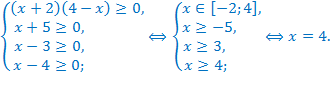
Так как ОДЗ состоит только из одного числа, то осталось проверить, является ли это число корнем исходного уравнения.
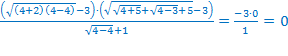. Значит, 
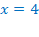действительно является корнем исходного уравнения.
Ответ: 
.
б)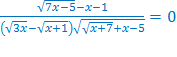 
Нахождение области допустимых значений усложняется за счёт второго множителя в знаменателе. Поэтому решим сначала уравнение 
, а затем проверим найденные корни для исходного уравнения.
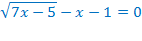
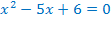
Выполним проверку.
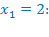
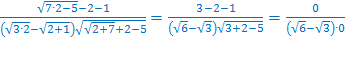. Полученное выражение не имеет смысла, т.к. в знаменателе оказался нуль, значит, 
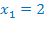не является корнем исходного уравнения.
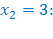
. Значит, 
является корнем исходного уравнения.
Ответ: 
.
8) Приведение иррациональных уравнений к числовым равенствам.
Ø Приведение иррациональных уравнений к неверным числовым равенствам.
В этом случае исходное уравнение корней не имеет.
|
|
|
Например, 
Как видно, в результате равносильных преобразований, получилось неверное числовое равенство. Это означает, что исходное уравнение корней не имеет.
Ответ: корней нет.
Ø Приведение иррациональных уравнений к верным числовым равенствам. Во время преобразований, ведущих к верному числовому равенству, необходимо следить за тем, что происходит с областью допустимых значений. Если она расширяется, то отсеиваем посторонние корни (в соответствии с ОДЗ); если область допустимых значений сужается, то лучше поискать другой способ решения данного уравнения.
Например,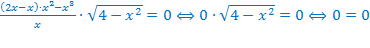 
.
Получилось верное равенство, значит, уравнение должно иметь бесконечно много корней. Однако, при использовании равносильных преобразований у нас расширилась область допустимых значений. Поэтому, необходимо найти ОДЗ исходного уравнения, это и будет его решением.
ОДЗ: 
Ответ: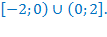 
9) Переход к модулям может быть использован на основании одного из свойств корня: 
, где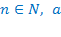 
– любое действительное число. Такое преобразование является равносильным и ОДЗ не изменяется.
|
|
|
Например, 
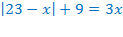
Воспользуемся определением модуля:
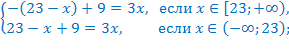
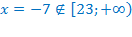, значит, единственным корнем уравнения является 
.
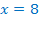Ответ: 
.
10) Преобразование иррациональных уравнений. Выполняя преобразования при решении иррациональных уравнений, необходимо помнить, что есть преобразования, которые сохраняют область допустимых значений, а есть преобразования, которые изменяют ОДЗ. Рассмотрим возможные преобразования.
· Замена выражений тождественно равными выражениями, не изменяющими ОДЗ.
К таким заменам относятся:
˗ перестановка местами слагаемых и множителей в обеих частях уравнения;
˗ раскрытие скобок в обеих частях уравнения;
˗ группировка слагаемых (множителей) в обеих частях уравнения;
˗ вынесение за скобки общего множителя;
˗ замена числовых выражений их значениями;
˗ выполнение действий с одночленами и многочленами, присутствующими в записи уравнения.
Обратите внимание, что приведение подобных слагаемых, сокращение дробей, замена нулём произведения или дроби с равным нулю числителем, может привести к изменению ОДЗ. Причём, появление посторонних корней можно откорректировать областью допустимых значений, а вот потерю корней откорректировать не получится. Поэтому, в таком случае, следует поискать другой способ решения уравнения.
|
|
|
Например, 
На первый взгляд уравнение кажется достаточно простым и многим придёт на ум идея представить выражение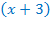 
в виде корня в квадрате 
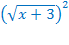. Тогда уравнение приобретает вид: 
. А теперь разберём, что мы получаем в этом случае. ОДЗ исходного уравнения: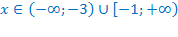 
. После преобразования ОДЗ станет: 
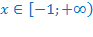. Мы получили сужение области допустимых значений, а это приводит к потере корней. Значит, такое преобразование выполнять нельзя.
Другие сделают другое преобразование: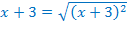 
. Но такое преобразование не будет тождественно равным, т.к. 
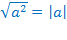, но никак не 
. Тогда, с учётом модуля, исходное уравнение будет представлено в виде системы двух уравнений, а это решение уже не будет оптимальным.
Значит, ищем другой подход к решению данного уравнения. Обращаем внимание на то, что в каждом из первых двух слагаемых присутствуют одинаковые выражения. Можно сделать замену переменной: 
, тогда 
и уравнение принимает вид: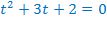 
Возвращаемся к исходной переменной:
|
|
|
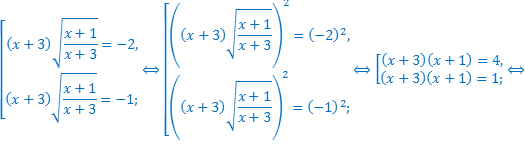
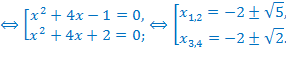
Произведём проверку.
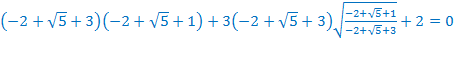
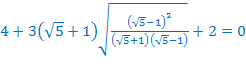
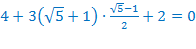
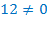
Значит,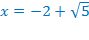 
– посторонний корень.
Аналогично проверяем остальные три значения х. Получаем, что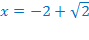 
– тоже посторонний корень. Значит, корнями исходного уравнения являются: 
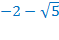и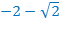 
Ответ: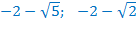 
· Прибавление (или вычитание) одного и того же числа к обеим частям уравнения.
Это равносильное преобразование, оно не изменяет область допустимых значений.
Например,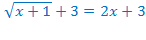 
Вычитаем из обеих частей уравнения .
ОДЗ: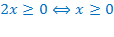 
.
Возводим в квадрат обе части уравнения.
Ответ: 
· Прибавление (вычитание) одного и того же выражения, не изменяющего ОДЗ, к обеим частям уравнения.
Например, 
ОДЗ: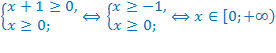 
Вычитаем из обеих частей уравнения слагаемое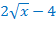 
и получаем уравнение:
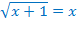
Так как правая часть этого уравнения должна быть неотрицательной, то область допустимых значений не изменилась, т.е. преобразование равносильно. Возведём в квадрат обе части уравнения.
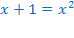
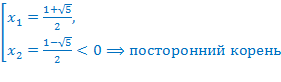
Ответ: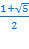 
· Перенесение слагаемых из одной части уравнения в другую с противоположным знаком.
Это преобразование всегда равносильное, область допустимых значений не изменяет.
Например,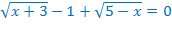 
ОДЗ: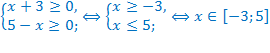 
Перенесём слагаемые 
в правую часть уравнения с противоположными знаками. Область допустимых значений не изменится.
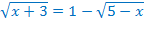
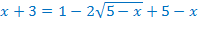
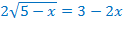
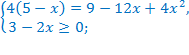
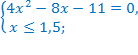
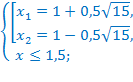
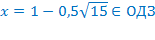
Ответ: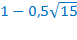 
· Умножение (деление) обеих частей уравнения на одно и то же, отличное от нуля, число.
Это равносильное преобразование, не изменяет области допустимых значений и используется, обычно, для перехода от дробных чисел к целым.
Например,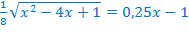 
ОДЗ: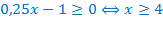 
Умножим обе части уравнения на , при этом ОДЗ не изменится.
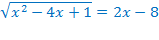
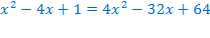
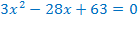
Ответ: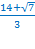 
· Умножение (деление) обеих частей уравнения на одно и то же выражение, не изменяющее ОДЗ, и не равное в этой области нулю.
Это преобразование равносильно тогда, когда выражение, на которое умножают или делят, не изменяет область допустимых значений и не обращается на этой области в нуль. При использовании этого преобразования, необходимо следить за изменением ОДЗ.
Например,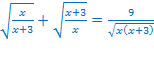 
ОДЗ: 
Сразу отметим, что преобразование, которое приводит исходное уравнение к виду: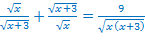 
не является равносильным, т.к. в этом случае сужается ОДЗ, что приводит к потере корней. Действительно, ОДЗ полученного уравнения:
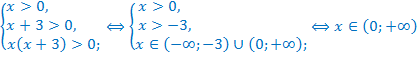
Поэтому такое преобразование недопустимо.
Мы поступим по-другому. Так как 
, то умножим на это выражение обе части уравнения. Получим:
. Это преобразование не изменило ОДЗ.
В левой части раскроем скобки, а в правой – умножим дробь на выражение. Как мы выяснили ранее, эти преобразования опять-таки не меняют ОДЗ, значит, равносильные.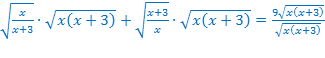 
.
Далее воспользуемся свойством корня из произведения и сокращением дробей. Это преобразование расширит ОДЗ, однако, мы сможем отсеять посторонние корни в соответствии с ОДЗ исходного уравнения.
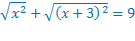
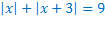
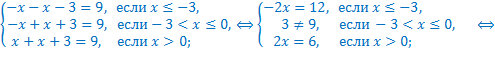
Оба найденных корня принадлежат ОДЗ исходного уравнения, значит, они являются корнями исходного уравнения.
Ответ: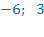 
· Возведение обеих частей уравнения в одну и ту же степень.
Это преобразование в общем случае не является равносильным, т.к. приводит к расширению ОДЗ, поэтому необходимо либо найти сразу ОДЗ, а затем отсеять посторонние корни, либо решить уравнение и в конце выполнить проверку найденных корней. Примеры таких преобразований присутствуют практически во всех ранее рассмотренных примерах.
На основании всего выше сказанного, подытожим:
Ø производите равносильные преобразования;
Ø следите за областью допустимых значений.
Дата добавления: 2022-06-11; просмотров: 120; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!