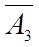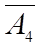Определить, в какой форме записана ЗЛП. Ответ обосновать.
Г.(1,2 пара) группа 1-ТОА-21/з
Тема: Решение задач линейного программирования симплекс-методом.
Вид занятия : лекция
Тип занятия : усвоения новых знаний
Цель:
• изучение идеи симплекс-метода для решения ЗЛП;
• изучение алгоритма симплекс-метода;
• формирование навыков самостоятельной работы по заданному алгоритму решения ЗЛП симплекс-методом;
• повторение форм моделей задач линейного программирования;
• повторение алгоритма перехода от одной формы задачи линейного программирования к другой;
• повторение алгоритма графического метода решения задач линейного программирования;
• формирование навыков самостоятельной работы по заданному алгоритму;
• закрепление, систематизация и обобщение знаний о задачах линейного программирования, формах моделей задач линейного программирования, о графическом методе решения задач линейного программирования;
воспитательная:
• формировать умения самостоятельно пополнять знания, пользоваться учебной литературой и др. источниками;
• воспитывать коммуникативную и информационную культуру студентов, культуру ведения записей, математической речи;
• формировать у студентов умения самоанализа и самооценки;
• развивать интерес к математике, техническим наукам и своей будущей профессии;
Развивающая:
• развивать аналитические и творческие способности студентов, обеспечивающие конкурентоспособность будущего специалиста на рынке труда;
• развивать умения выбора, обоснования, классификации по признакам, принятия решений;
• формировать понимание ответственности за принятые решения;
• обеспечить условия для формирования рациональных приемов мыслительной деятельности студентов с целью успешного освоения учебной программы дисциплины и дальнейшей успешной профессиональной деятельности.
В результате изучения темы студент должен знать:
ü Постановку ЗЛП, модели ЗЛП,
ü алгоритм перехода от одной формы ЗЛП к другой,
ü алгоритм графического метода решения ЗЛП;
ü алгоритм симплекс-метода.
В результате изучения темы студент должен уметь:
ü По заданному алгоритму осуществлять переход от одной формы ЗЛП к другой,
ü используя алгоритм симплекс-метода решения ЗЛП, по заданному образцу решать ЗЛП симплекс- методом.
Литературные источники:
1. Богомолов Н.В. Практические занятия по математике. - М.: Дрофа - 2010.- 400 с.
2. Богомолов Н.В., Сергиенко Л.Ю. Сборник дидактических заданий по математике. - М.-Дрофа-2009.
3. Григорьев С.Г. Математика: учебник для студентов сред. проф. учреждений / С.Г. Григорьев, С.В. Задулина; под ред. В.А. Гусева. - 2-е изд., стер. - М.: Издательский центр «Академия», 2007. - 384 с.
4. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. - 4-е изд., перераб. и доп. - М.: ЮНИТИ-ДАНА, 2010. - 573 с.
5. Спирина М.С. Теория вероятностей и математическая статистика: учебник для студ. учреждений сред. проф. образования / М.С. Спирина, П.А. Спирин. - М.: Издательский центр «Академия», 2007. - 352 с.
6. Спирина М.С. Дискретная математика: учебник для студ. учреждений сред. проф. образования / М.С. Спирина, П.А. Спирин. - М.: Издательский центр «Академия», 2010. - 368 с.
7. П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова Высшая математика в упражнениях и задачах. Часть 1 и 2. - М.: Высшая школа, 2008.
8. Н.В. Богомолов Задачи по математике с решениями. - М.: Высшая школа, 2006
9. Н.В. Богомолов, П.И. Самойленко Математика. - М.: Дрофа, 2004
10. З.И. Гурова, С.Н. Каролинская, А.П. Осипова Математический анализ. Начальный курс с примерами и задачами- М.: ФИЗМАТЛИТ, 2002
11. И.Д. Пехлецкий Математика. - М.: Мастерство, 2001
12. В.Ф. Бутузов, Н.И. Крутицкая. Математичесий анализ в вопросах и задачах. - М.: Физматлит, 2000
1. Актуализация опорных знаний
1.1Устный опрос:
а) назвать формы моделей задач линейного программирования , дать характеристику каждой модели,
б)охарактеризовать а лгоритм перехода от одной формы задачи линейного программирования к другой,
в)описать алгоритм графического метода решения задач линейного программирования.
г) Продолжить предложение:
1) Графический метод используется для решения задачи линейного программирования, записанной в форме…
2) Для задачи линейного программирования, записанной в канонической форме, используется метод …
3) Симплексный метод используется для задачи линейного программирования, записанной в форме…
4) Переход от одной формы задачи линейного программирования к другой осуществляется в последовательности…
5) Условие неотрицательности на все переменные накладываются в форме записи задачи линейного программирования…
6) Наличие только жестких условий в системе ограничений присущи…
Определить, в какой форме записана ЗЛП. Ответ обосновать.
1) z = –2 x 1 – x 3 → min
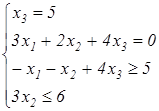
x 1 ≥ 0, x 3 ≤ 0
2) z = –3 x 3 – 6 x 4 –2 → max
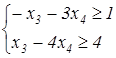
x 3 ≥ 0, x 4 ≥ 0
2. Изучение нового материала.
Идея симплекс-метода .
Симплекс-метод применяется для решения любых задач линейного программирования. Это универсальный, точный метод. Он принадлежит к категории методов последовательного улучшения плана.
- ОДЗ ЗЛП – выпуклое множество.
- Целевая функция принимает свое оптимальное значение в одной из целевых точек
 Идея симплекс-метода в том, что он дает способ целенаправленного перебора части угловых точек (метод последовательного улучшения опорного плана).
Идея симплекс-метода в том, что он дает способ целенаправленного перебора части угловых точек (метод последовательного улучшения опорного плана).
| Последовательное улучшение плана идет по точкам А1, А2, А3, А4, А5 А6, А7 не будут исследоваться z (A1), z (A2), z (A3), z (A4), z (A5) |
Идея симплекс-метода базируется на предположениях:
1) указывается способ построения начального опорного плана.
2) указывается критерий, с помощью которого оценивается проверяемый опорный план на оптимальность
3) если опорный план не оптимален, указывается способ перехода к новому опорному плану, более близкому к оптимальному.
Алгоритм симплекс-метода
1) проверяется каноническая форма
2) выделяется начальный опорный план и значение целевой функции для него
3) строится симплекс-таблица
4) проверяется значения оценок оптимальности в индексной строке. Если нет положительных оценок, то получим оптимальное решение
5) в базис вводится вектор, которому соответствует наибольшая положительная оценка. Этот столбец называется разрешающим
6) из базиса выводится вектор, которому соответствует симплексное отношение
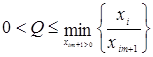 Строка называется разрешающей
Строка называется разрешающей
7) Строим новую симплекс-таблицу
3. Закрепление изученного материала.
Пример № 1. Решить ЗЛП симплекс-методом z = 2 x 1 – x 2 + 3 x 3 – 2 x 4 → max
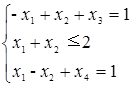
х j ≥ 0 , j = 
Решение.
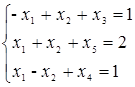
z ′ = – z = – 2х1 + х2 – 3х3 + 2х4 + 0·х5 → min
х j ≥ 0, j = 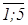
Р1 =  Р2 =
Р2 =  Р3 =
Р3 = 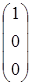 Р4 =
Р4 =  Р5 =
Р5 = 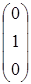
| Б | СБ | АБ | 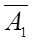
| 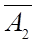
| 
| 
| 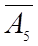
| исходный опорный план z ' ( | |
| – 2 | 1 | –3 | 2 | 0 | |||||
|
| – 3 | 1 | – 1 | 1 | 1 | 0 | 0 | ||
|
| 0 | 2 | 1 | 1 | 0 | 0 | 1 | ||
|
| 2 | 1 | 1 | – 1 | 0 | 1 | 0 | → разрешающая строка | |
| z'j – cj | – 1 | 7 | – 6 | 0 | 0 | 0 | индексная (оценочная) строка | ||
|
| ↑ |
| |||||||
| разрешающий столбец | |||||||||
Вместо  вводим в базис
вводим в базис 
Симплексное отношение Q = min  = 1
= 1
Таблица 2
| Б | СБ | АБ | 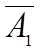
| 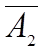
| 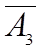
| 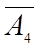
| 
| |
| – 2 | 1 | –3 | 2 | 0 | ||||

| – 3 | 2 | 0 | 0 | 1 | 1 | 0 | |
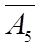
| 0 | 1 | 0 | 2 | 0 | – 1 | 1 | → разрешающая строка |

| – 2 | 1 | 1 | – 1 | 0 | 1 | 0 | |
| z'j – cj | – 8 | 0 | 1 | 0 | – 7 | 0 | ||
| ↑ |
| |||||||
| разрешающий столбец | ||||||||
Вместо 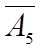 вводим в базис
вводим в базис 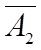
Симплексное отношение Q = min 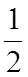 =
= 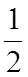
Таблица 3
| Б | СБ | АБ | 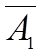
| 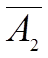
| 
| 
| 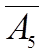
|
| – 2 | 1 | –3 | 2 | 0 | |||

| – 3 | 2 | 0 | 0 | 1 | 1 | 0 |
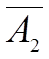
| 1 | 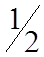
| 0 | 1 | 0 | – 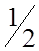
| 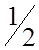
|
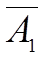
| – 2 | 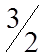
| 1 | 0 | 0 | 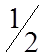
| 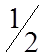
|
| z'j – cj | – 
| 0 | 0 | 0 | – 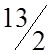
| – 
| |
| ↑ оптимальное значение целевой функции | |||||||
Оптимальный план
х1 = 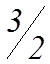 , х2 =
, х2 = 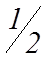 , х3 = 2, х4 = 0, х5 = 0.
, х3 = 2, х4 = 0, х5 = 0.
Задача была преобразована, значит,
х opt =( 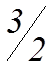 ;
;  ; 2; 0)
; 2; 0)
zmax = 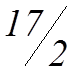
Пример № 2. Решить задачу симплекс-методом:
Найти max Z = – 2х1 + х2 при 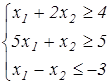
Решение.
I этап
а) если среди свободных членов в системе ограничения есть отличные, то соответствующие ограничения умножить на ( – 1). В нашем случае это правило относится к III ограничению.
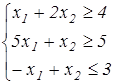
если в ограничении есть неравенство, тогда вводят дополнительные переменные, превращающие их в уравнения

Мы имеем канонический вид задачи:

min (– Z ) = 2х1 – х2
б) в ограничениях, где дополнительные переменные вычитаются, прибавляют искусственные переменные с последовательными номерами х6, х7, их также прибавляют в целевую функцию:
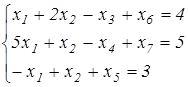 ,
,
где х1, х2 – главные переменные;
х3, х4, х5 – дополнительные переменные;
х6, х7 – искусственные переменные.
min (– Z ) = 2х1 – х2 = Мх6 + Мх7
в) запишем векторы и коэффициенты при неизвестных и вектор свободных членов.
Р1 = 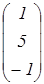 Р2 =
Р2 = 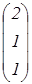 Р3 =
Р3 = 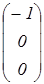 Р4 =
Р4 = 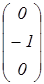 Р5 =
Р5 =  Р6 =
Р6 = 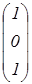 Р7 =
Р7 =  Р8 =
Р8 = 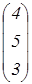
г) строим первую симплекс-таблицу:
| Базис | С | Р0 | 2 | – 1 | 0 | 0 | 0 | М | М | СВ |
| Р1 | Р2 | Р3 | Р4 | Р5 | Р6 | Р7 | ||||
| Р6 | М | 4 | 1 | 2 | – 1 | 0 | 0 | 1 | 0 | 4 |
| Р7 | М | 5 | 5 | 1 | 0 | – 1 | 0 | 0 | 1 | 1 |
| Р5 | О | 3 | – 1 | 1 | 0 | 0 | 1 | 0 | 0 | – |
| Z – строка | 0 | – 2 | 1 | 0 | 0 | 0 | 0 | 0 | ||
| M - строка | 9 | 6 | 3 | – 1 | – 1 | 0 | 0 | 0 | ||
Заполним таблицу:
1. Заносим все векторы ( Р і ).
2. в самой верхней строке записываем коэффициенты целевой функции при неизвестных.
3. Первичным базисом берем единичные векторы, образующие единичную матрицу, в данном случае Р6, Р7, Р5.
4. В столбец С переносят из верхней строки числа базисных векторов.
5. Для того, чтобы получить элементы последних двух строк, вектор С умножают последовательно на векторы Р0, … Р7 и от произведения вычитают числа из верхней строки.
| СР0 – О = 4М + 5М +3О = 9М | СР1 = М + 5М + (– 1)О – 2 = 6М – 2 |
| СР2 + 1 = 2М + М + 1О – (– 1) = 3М + 1 | СР3 – О = – М – О = – М и т.п. |
В М строку записывают коэффициенты при М, а в строку Z – коэффициенты без М.
ІІ этап. Проверка оптимальности решения.
а) Критерий оптимальности. Функция достигает минимума, когда среди элементов М-строки (а потом Z-строки, начиная со ІІ-ой), нет положительных чисел. В противном случае нужно оптимизировать решение. Согласно таблице 1 решение не является оптимальным.
б) Тогда находим ключевой столбец – по наибольшему положительному числу в М-строке (а потом Z-строки, начиная со ІІ-го. Ключевой столбец показывает, какой вектор войдет в новый базис) у нас наибольшее М = 6, в новый базис вводим вектор Р1.
в) Находим симплексное отношение, для чего элементы Р0: отрицательные элементы ключевого столбца (на положительные и нули не разделяются). Ключевой столбец берется по min СВ = 1. Ключевая строка вторая, базис покидает вектор Р7.
г) Элемент, стоящий на пересечении ключевой строки и ключевого столбца, называется генеральным. В таблице 1 = 5 он обозначен.
III этап. Построение нового решения (таблица 2)
а) Формирование нового базиса изменяя один вектор. В данном случае новый базис из векторов Р6, Р1 и Р7. Так как Р7 – искусственный вектор, то выбрасывают и М-строку.
б) Столбец С заполняют по правилу, указанному ранее – верхней строки.
в) Вычисления ведут таким образом:
1. Элементы ключевой строки делят на генеральный элемент и записывают в новую таблицу;
2. Ключевой столбец заполняют нулями;
3. Если в ключевой строке есть нули, то их столбцы переносятся без изменений.
4. Последние элементы находят по правилу прямоугольника. Для его построения в предыдущей таблице старый элемент соединяют с ключевой строкой и ключевым столбцом, а потом по строке и столбцу ведут до генерального элемента.
Таблица 2
| Базис | С | Р0 | 2 | – 1 | 0 | 0 | 0 | М | СВ |
| Р1 | Р2 | Р3 | Р4 | Р5 | Р6 | ||||
| Р6 | М | 3 | 0 | 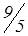
| – 1 | 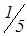
| 0 | 1 | 
|
| Р7 | 2 | 1 | 1 | 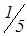
| 0 | 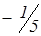
| 0 | 0 | 5 |
| Р5 | 0 | 4 | 0 | 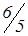
| 0 | 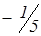
| 1 | 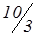
| |
| Z – строка | 2 | 0 | 1 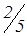
| 0 | – 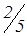
| 0 | 0 | ||
| M - строка | 3 | 0 | 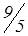
| – 1 | 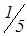
| 0 | 0 | ||



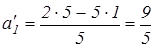
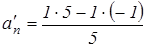
3М + 2 – 0 = 3М + 2 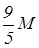 +
+ 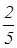 – (– 1) =
– (– 1) = 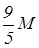 +
+ 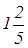 и т.д.
и т.д.
Проверка показала, что в таблице 2 условия оптимальности не выполняются.
Снова ключевой столбец Р2. Находим симплексные отношения:
СВ1 = 3 :  =
= 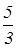 , СВ2 = 1 :
, СВ2 = 1 :  , СВ1 = 4 :
, СВ1 = 4 : 
Ключевая строка I. СВmin = 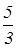 . В новый базис вводится вектор Р2, а его покидает вектор Р6. Генеральный элемент
. В новый базис вводится вектор Р2, а его покидает вектор Р6. Генеральный элемент  , т.к. Р6 выводится из базиса, то М будет отсутствовать.
, т.к. Р6 выводится из базиса, то М будет отсутствовать.
Таблица 3
| Базис | С | Р0 | 2 | – 1 | 0 | 0 | 0 | СВ |
| Р1 | Р2 | Р3 | Р4 | Р5 | ||||
| Р6 | – 1 | 
| 0 | 1 | – 
| 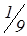
| 0 | – |
| Р7 | 2 | 
| 1 | 0 | 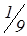
| – 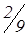
| 0 | 6 |
| Р5 | 0 | 2 | 0 | 0 | 
| 
| 1 | 3 |
| Z – строка | 
| 0 | 0 | 
| – 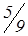
| 0 | ||
3 :  =
= 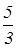
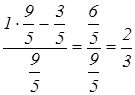 Z-строка
Z-строка
– 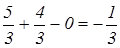
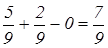 –
– 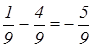
В столбце 3 не выполняются условия оптимальности. СВ1 = не имеет – 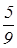 < 0
< 0
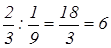 2 :
2 : 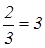 . Из базиса выводим вектор Р5, а в базис будет введен Р3; генеральный элемент
. Из базиса выводим вектор Р5, а в базис будет введен Р3; генеральный элемент  ; построим таблицу 4:
; построим таблицу 4:
Таблица 4
| Базис | С | Р0 | 2 | – 1 | 0 | 0 | 0 | СВ |
| Р1 | Р2 | Р3 | Р4 | Р5 | ||||
| Р2 | – 1 | 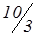
| 0 | 1 | 0 | 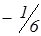
| 0 | |
| Р7 | 2 | 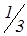
| 1 | 0 | 0 | 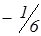
| 0 | |
| Р5 | 0 | 3 | 0 | 0 | 1 | 
| 1 | |
| Z – строка | 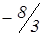
| 0 | 0 | 0 | 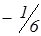
| 0 | ||
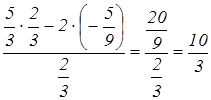
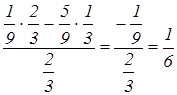
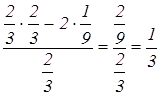
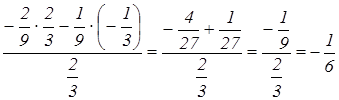
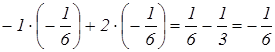
Условия оптимальности выполняются. Оптимальное решение имеет вид:
Х1 = 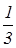 Х2 =
Х2 = 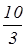 min (– Z ) = –
min (– Z ) = – 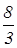 max =
max = 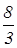
Задание:
1. Изучив опорный конспект, ответить на вопросы:
Ø Назвать, в каких формах существуют задачи линейного программирования (ЗЛП), в чем особенности каждой из форм;
Ø Описать алгоритм перехода от одной формы ЗЛП к другой;
Ø Охарактеризовать алгоритм графического метода решения задач линейного программирования;
Ø Сформулировать идею симплекс-метода;
Ø Охарактеризовать симплекс-метод решения ЗЛП.
2. Внимательно разобрать образцы решенных примеров, записать их в тетрадь.
3. Выполнить письменно в тетради задания №1.1 и №1.2 из раздела «Актуализация опорных знаний», оценить по 5-ти балльной системе свою работу. Работу и оценку предъявить лично на занятии после завершения карантина.
4. По образцу выполнить аналогичное задание домашней контрольной работы. Задание для домашней контрольной работы необходимо взять из «Методических рекомендаций», по порядковому номеру в списке группы. Можно выполнить в обычной тетради, сфотографировать или решить с использованием ПК и выслать на электронную почту преподавателя l.grig1@mail.ru.
Дата добавления: 2022-06-11; просмотров: 23; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

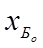 = (0, 0, 1, 1, 2)
= (0, 0, 1, 1, 2)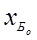 ) = – 1
) = – 1