Пример применения производящих функций в комбинаторике.
Производящие функции.
Определение 1: Пусть дана числовая последовательность: 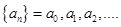 Образуем формальный степенной ряд с этими коэффициентами:
Образуем формальный степенной ряд с этими коэффициентами:  . Он называется производящей функцией данной последовательности. Если этот ряд сходится в некоторой области к функции
. Он называется производящей функцией данной последовательности. Если этот ряд сходится в некоторой области к функции 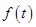 , то эту функцию тоже называют производящей для последовательности чисел
, то эту функцию тоже называют производящей для последовательности чисел 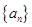 .
.
Метод производящих функций основан на соответствии между операциями с членами последовательностей (коэффициентами степенного ряда) и функциями, выражающими сумму этого ряда в случае его сходимости. Подробное обоснование этих соответствий будет дано при изучении теории рядов.
1) Найдём производящую функцию последовательности, все члены которой равны 1.
Рассмотрим степенной ряд  , члены которого можно рассматривать как геометрическую прогрессию со знаменателем
, члены которого можно рассматривать как геометрическую прогрессию со знаменателем  . Этот степенной ряд при условии
. Этот степенной ряд при условии  сходится к своей сумме
сходится к своей сумме  .
.
Значит, функция 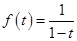 является производящей для последовательности чисел
является производящей для последовательности чисел 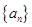 , где
, где 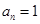 для всех
для всех 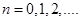
2) Если производящая функция последовательности 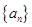 , равная
, равная  , является дифференцируемой, то её производная
, является дифференцируемой, то её производная 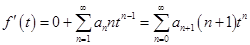 является производящей функцией для последовательности
является производящей функцией для последовательности 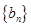 , такой что
, такой что 
Например, дифференцируя функцию 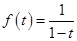 и соответствующий ей степенной ряд
и соответствующий ей степенной ряд  , можно получить равенство:
, можно получить равенство:
 .
.
Значит, функция 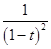 является производящей для последовательности чисел
является производящей для последовательности чисел 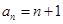 .
.
Умножив эту функцию и её степенной ряд на 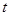 , получим равенство
, получим равенство 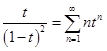 , из которого следует, что функция
, из которого следует, что функция 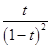 является производящей для последовательности
является производящей для последовательности 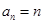 .
.
|
|
|
3) Из формулы бинома Ньютона следует:
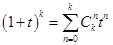 , т.е. многочлен
, т.е. многочлен  является производящей для последовательности
является производящей для последовательности 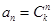 при
при  ,
,  при
при  .
.
Вообще, производящая функция последовательности является многочленом тогда и только тогда, когда все члены последовательности, начиная с некоторого, равны нулю.
4) Сумме и разности и любой линейной комбинации производящих функций соответствуют сумма и разность и аналогичная линейная комбинация их порождающих последовательностей.
5) Если  - производящая функция последовательности
- производящая функция последовательности 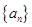 ,
,
то  является производящей функцией для последовательности
является производящей функцией для последовательности 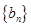 ,
,
где 
Составим таблицу соответствия некоторых последовательностей и их производящих функций
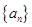
| 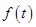
|
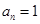
| 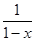
|
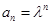
| 
|
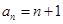
| 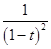
|
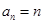
| 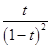
|
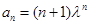
| 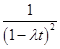
|
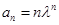
| 
|
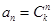 при при  , ,  при при 
| 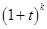
|
Применение производящих функций для решения рекуррентных уравнений.
Определение 2. Последовательность 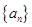 называется заданной рекуррентно, если при
называется заданной рекуррентно, если при  значение члена последовательности
значение члена последовательности 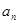 является функцией от
является функцией от 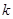 предыдущих членов последовательности
предыдущих членов последовательности 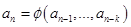 . Если при этом заданы значения первых
. Если при этом заданы значения первых 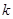 членов
членов 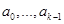 , последовательность определена однозначно.
, последовательность определена однозначно.
|
|
|
При помощи производящих функций для рекуррентно заданной последовательности можно получить общую формулу, выражающую зависимость 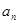 от
от 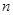 .
.
Рассмотрим рекуррентное соотношение второго порядка.
Покажем, что если последовательность 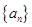 определяется соотношением
определяется соотношением 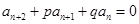 , где p, q – некоторые числа, то ее производящая функция
, где p, q – некоторые числа, то ее производящая функция 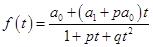
Рассмотрим формальный степенной ряд  и сложим почленно три равенства:
и сложим почленно три равенства:
 ,
,
 ,
,
 .
.
Получим, что 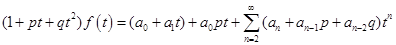 .
.
Из рекуррентного соотношения при 
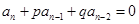 , поэтому
, поэтому
 , откуда получаем выражение для производящей функции
, откуда получаем выражение для производящей функции 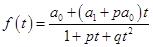 . С помощью неё можно найти общую формулу члена последовательности
. С помощью неё можно найти общую формулу члена последовательности 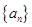 .
.
Пример 1:
Найти последовательность, заданную рекуррентными отношениями
a0 = 0, a1 = -6, an = 5an-1 -4an-2.
Перепишем рекуррентное отношение в виде  (
(  )
)
Производящая функция последовательности 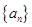 равна
равна
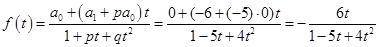 .
.
Разложим её на простейшие дроби:
 и представим их в виде степенных рядов
и представим их в виде степенных рядов
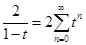 ,
, 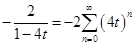 . Получаем, что производящая функция равна
. Получаем, что производящая функция равна 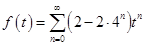 . Откуда находим общую формулу для члена последовательности:
. Откуда находим общую формулу для члена последовательности:
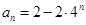
Пример 2:
Найти последовательность, заданную рекуррентными отношениями
|
|
|
a0 = 1, a1 =5 , an = 4an-1 -4an-2.
Перепишем рекуррентное отношение в виде 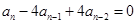 (
(  )
)
Производящая функция последовательности 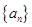 равна
равна
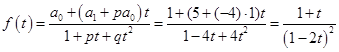 .
.
Представим её в виде
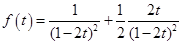 .
.
В этой сумме первое слагаемое является производящей функцией для последовательности  , а второе - для последовательности
, а второе - для последовательности  (см. таблицу).
(см. таблицу).
Откуда находим общую формулу для члена последовательности:
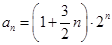
Пример применения производящих функций в комбинаторике.
Определение 3. Произведением производящих функций  и
и 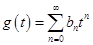 называется производящая функция
называется производящая функция  , для которой коэффициенты
, для которой коэффициенты
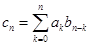 , то есть
, то есть
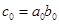 ,
,
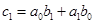 ,
,
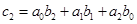 ,
,
и т. д.
Если ряды для производящих функций 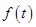 и
и 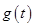 сходятся абсолютно, то
сходятся абсолютно, то  совпадает с обычным алгебраическим произведением
совпадает с обычным алгебраическим произведением 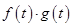 .
.
Последовательно можно определить произведение для любого числа производящих функций.
Выясним комбинаторный смысл умножения производящих функций.
Пусть 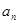 и
и 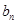 - количество некоторых комбинаторных объектов мощности
- количество некоторых комбинаторных объектов мощности 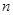 из множеств
из множеств  и
и 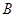 , тогда количество
, тогда количество 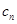 таких объектов мощности
таких объектов мощности 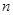 в объединении
в объединении  может быть найдено по формуле
может быть найдено по формуле 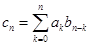 .
.
Пример 3. В урне находятся 3 жёлтых и 5 зелёных шаров. Сколькими способами можно выбрать 5 шаров, если один из них должен быть зелёным? (Шары одинакового цвета считаем неразличимыми между собой, выборки считаются различными, если отличаются по количеству шаров одного цвета.)
|
|
|
Обозначим 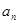 число способов выбрать
число способов выбрать 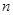 жёлтых шаров,
жёлтых шаров, 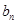 - число способов выбрать
- число способов выбрать 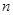 зелёных шаров. В условиях задачи
зелёных шаров. В условиях задачи 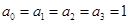 ,
,  для
для  ,
,  ,
, 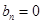 для
для 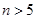 .
.
Производящие функции для последовательностей 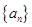 и
и 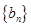 равны соответственно
равны соответственно  и
и 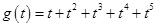 . Их произведение
. Их произведение 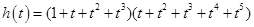 является производящей функцией для последовательности
является производящей функцией для последовательности 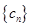 , где
, где 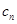 - число различных наборов из
- число различных наборов из 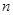 жёлтых и зелёных шаров. Для того, чтобы узнать, сколькими способами можно выбрать 5 шаров, нам нужно найти
жёлтых и зелёных шаров. Для того, чтобы узнать, сколькими способами можно выбрать 5 шаров, нам нужно найти 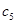 . Раскрывая скобки, получаем, что
. Раскрывая скобки, получаем, что  .
.
Пример 4. В урне находятся 5 красных, 2 синих, 3 жёлтых и 5 зелёных шаров. Сколькими способами можно выбрать 5 шаров, если один из них должен быть жёлтым?
Как и в предыдущей задаче, производящая функция для последовательности 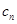 - числа различных наборов из
- числа различных наборов из 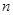 шаров является произведением производящих функций для возможного числа шаров каждого цвета и равна
шаров является произведением производящих функций для возможного числа шаров каждого цвета и равна 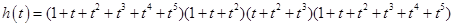
Далее нужно преобразовать это произведение так, чтобы можно было найти коэффициент при пятой степени. Не обязательно для этого проводить полное раскрытие скобок. Можно поступить, например, так: перемножаем первый многочлен со вторым, третий – с четвёртым, получаем
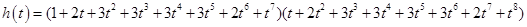 ,
,
находим коэффициент при  , суммируя произведения коэффициентов в скобках при степенях, в сумме дающих 5.
, суммируя произведения коэффициентов в скобках при степенях, в сумме дающих 5.
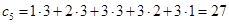
Дата добавления: 2022-06-11; просмотров: 454; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
