Гипербола. Каноническое уравнение гиперболы. Свойства гиперболы.
Гипербола. Каноническое уравнение гиперболы. Свойства гиперболы.
Гиперболой называется множество всех точек плоскости, абсолютная величина разности расстояний от каждой из которых до данных точек F1 и F2 равна длине данного отрезка PQ , причем PQ < F1F2. Точки F1 и F2 называются фокусами гиперболы, а расстояние между ними – фокальным расстоянием.
Если точка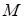 
лежит на гиперболе, то отрезки F1М и F2М называют фокальными радиусами точки М. Обозначим F1F2=2с, PQ=2а. В силу определения а<с, обозначим
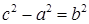. (8)
Рассмотрим специально выбранную систему координат, в которой фокусы F1и F2 расположены на оси абсцисс симметрично относительно начала координат.Тогда фокусы имеют координаты 
. Пусть точка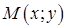 
– произвольная точка гиперболы γ, тогда из определения гиперболы следует:
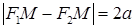, (9)
или в координатах
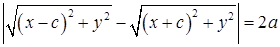. (10)
Возводя обе части равенства в квадрат и проводя тождественные преобразования, получим
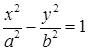, (11)
где с2-а2= b 2.
Тем самым доказано, что координаты любой точки гиперболы удовлетворяют уравнению (11). Можно доказать обратное: точка, координаты которой удовлетворяют уравнению (11), принадлежат гиперболе, т.е. выполняется равенство: 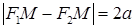. Подставим в формулы F1M и F2M значение у2 из уравнения (11), получим: 
, 
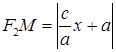. Так как 
, 
, то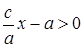 
, если х>0 или 
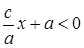, если х<0. Тогда выполняется равенство (9), т.е. точка М 
γ. Итак, уравнение (11) является уравнением гиперболы. Оно называется каноническим уравнением гиперболы.
Из канонического уравнения гиперболы так же, как и в случае с уравнением эллипса, можно вывести геометрические свойства гиперболы.
1. Координаты точки О(0;0) не удовлетворяют уравнению гиперболы, т.е. гипербола не проходит через начало координат.
2. Так как переменные х и у входят в уравнение (11) в четных степенях, то гипербола симметрична относительно осей координат и начала координат.
3. Гипербола пересекает ось Ох в точках А1(а;0) и А2(-а;0). Точки А1 и А2 называются вершинами гиперболы, а отрезок А1А2 – ее действительной осью. Ось Оу гипербола не пересекает (пересекает в двух мнимых точках B1(0; b) и B2(0;- b)), ее называют мнимой осью.
4. Из уравнения (11) следует, что , т.е. х≥а или х≤ -а и, значит, внутри полосы, определяемой прямыми х=а и х= - а, точек гиперболы нет.
5. Для точки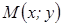 
первой четверти ( 
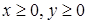) имеем: 
. При возрастании х от а до бесконечности ордината y точки М возрастает от 0 до бесконечности.
6. Рассмотрим взаимное расположение прямой, проходящей через начало координат, и гиперболы:
Решение системы сводится к решению уравнения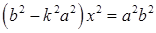 
. Возможны следующие случаи:
а) если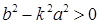 
, то уравнение имеет два действительных корня, значит, прямая пересекает гиперболу в двух точках;
б) если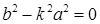 
, то уравнение решений не имеет, прямая не пересекает гиперболу;
в) если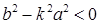 
, то уравнение действительных корней не имеет, прямая и гипербола не имеют общих точек.
Прямые l 1 и l 2, , заданные уравнениям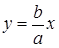и
и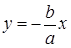 
, (12)
не имеют общих точек с гиперболой и называются асимптотами гиперболы. Гипербола γ лежит внутри тех вертикальных углов, образованных ее асимптотами, которым принадлежат фокусы, а расстояние от точки М γ до соответствующей асимптоты стремится к нулю, когда точка стремится по гиперболе в бесконечность. Пусть точка М имеет координаты (х; y0). Возьмем на прямой l 1 точку 
. Будем считать, что точки лежат в первой координатной четверти, т.е.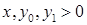 
. Имеем
, 
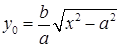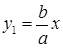. (13)
Следовательно,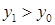 
. Найдем разность ординат
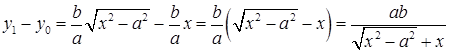. (14)
Из равенства (14) следует, что при х, стремящемся к бесконечности, разность ординат точек стремится к нулю. И точка М по мере возрастания ее абсциссы неограниченно приближается к асимптоте .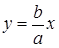
Эксцентриситетом гиперболы называется число, равное отношению фокального расстояния к действительной оси. Для гиперболы, заданной уравнением (11) это число равно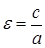 
. Так как с>а, то ε >1. Так как 
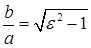,то среди гипербол, имеющих одну и ту же действительную полуось, но разные эксцентриситеты, более вытянута вдоль оси Оу та, у которой эксцентриситет больше.
 |
Замечание 1. Гипербола, полуоси которой равны a = b, называется равносторонней. Ее уравнение имеет вид х2–у2=а2. Асимптоты равносторонней гиперболы перпендикулярны.
Замечание 2. Если ось Ох - мнимая ось гиперболы, а ось О y - действительная, то каноническое уравнение гиперболы имеет вид
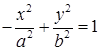
В этом случае фокусы гиперболы лежат на оси Oy.
Замечание 3. Гиперболы, заданные уравнениями
,
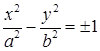называются сопряженными. Асимптоты для этих гипербол одни и те же.
Гипербола. Каноническое уравнение гиперболы. Свойства гиперболы.
Гиперболой называется множество всех точек плоскости, абсолютная величина разности расстояний от каждой из которых до данных точек F1 и F2 равна длине данного отрезка PQ , причем PQ < F1F2. Точки F1 и F2 называются фокусами гиперболы, а расстояние между ними – фокальным расстоянием.
Если точка 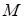лежит на гиперболе, то отрезки F1М и F2М называют фокальными радиусами точки М. Обозначим F1F2=2с, PQ=2а. В силу определения а<с, обозначим
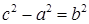. (8)
Рассмотрим специально выбранную систему координат, в которой фокусы F1и F2 расположены на оси абсцисс симметрично относительно начала координат.Тогда фокусы имеют координаты . Пусть точка 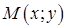– произвольная точка гиперболы γ, тогда из определения гиперболы следует:
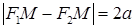, (9)
или в координатах
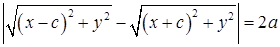. (10)
Возводя обе части равенства в квадрат и проводя тождественные преобразования, получим
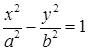, (11)
где с2-а2= b 2.
Тем самым доказано, что координаты любой точки гиперболы удовлетворяют уравнению (11). Можно доказать обратное: точка, координаты которой удовлетворяют уравнению (11), принадлежат гиперболе, т.е. выполняется равенство: 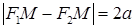. Подставим в формулы F1M и F2M значение у2 из уравнения (11), получим: , 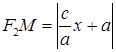. Так как , , то 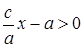, если х>0 или 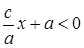, если х<0. Тогда выполняется равенство (9), т.е. точка М γ. Итак, уравнение (11) является уравнением гиперболы. Оно называется каноническим уравнением гиперболы.
Из канонического уравнения гиперболы так же, как и в случае с уравнением эллипса, можно вывести геометрические свойства гиперболы.
6. Координаты точки О(0;0) не удовлетворяют уравнению гиперболы, т.е. гипербола не проходит через начало координат.
7. Так как переменные х и у входят в уравнение (11) в четных степенях, то гипербола симметрична относительно осей координат и начала координат.
8. Гипербола пересекает ось Ох в точках А1(а;0) и А2(-а;0). Точки А1 и А2 называются вершинами гиперболы, а отрезок А1А2 – ее действительной осью. Ось Оу гипербола не пересекает (пересекает в двух мнимых точках B1(0; b) и B2(0;- b)), ее называют мнимой осью.
9. Из уравнения (11) следует, что , т.е. х≥а или х≤ -а и, значит, внутри полосы, определяемой прямыми х=а и х= - а, точек гиперболы нет.
10. Для точки 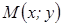первой четверти ( 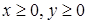) имеем: . При возрастании х от а до бесконечности ордината y точки М возрастает от 0 до бесконечности.
6. Рассмотрим взаимное расположение прямой, проходящей через начало координат, и гиперболы:
Решение системы сводится к решению уравнения 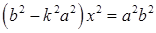. Возможны следующие случаи:
а) если 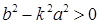, то уравнение имеет два действительных корня, значит, прямая пересекает гиперболу в двух точках;
б) если 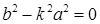, то уравнение решений не имеет, прямая не пересекает гиперболу;
в) если 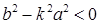, то уравнение действительных корней не имеет, прямая и гипербола не имеют общих точек.
Прямые l 1 и l 2, , заданные уравнениям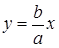и
и 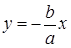, (12)
не имеют общих точек с гиперболой и называются асимптотами гиперболы. Гипербола γ лежит внутри тех вертикальных углов, образованных ее асимптотами, которым принадлежат фокусы, а расстояние от точки М γ до соответствующей асимптоты стремится к нулю, когда точка стремится по гиперболе в бесконечность. Пусть точка М имеет координаты (х; y0). Возьмем на прямой l 1 точку . Будем считать, что точки лежат в первой координатной четверти, т.е. 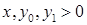. Имеем
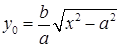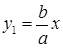, . (13)
Следовательно, 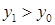. Найдем разность ординат
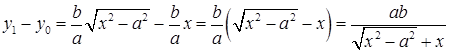. (14)
Из равенства (14) следует, что при х, стремящемся к бесконечности, разность ординат точек стремится к нулю. И точка М по мере возрастания ее абсциссы неограниченно приближается к асимптоте .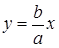
Эксцентриситетом гиперболы называется число, равное отношению фокального расстояния к действительной оси. Для гиперболы, заданной уравнением (11) это число равно 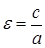. Так как с>а, то ε >1. Так как 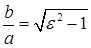,то среди гипербол, имеющих одну и ту же действительную полуось, но разные эксцентриситеты, более вытянута вдоль оси Оу та, у которой эксцентриситет больше.
| |
Замечание 1. Гипербола, полуоси которой равны a = b, называется равносторонней. Ее уравнение имеет вид х2–у2=а2. Асимптоты равносторонней гиперболы перпендикулярны.
Замечание 2. Если ось Ох - мнимая ось гиперболы, а ось О y - действительная, то каноническое уравнение гиперболы имеет вид
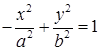
В этом случае фокусы гиперболы лежат на оси Oy.
Замечание 3. Гиперболы, заданные уравнениями
,
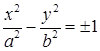называются сопряженными. Асимптоты для этих гипербол одни и те же.
Дата добавления: 2022-06-11; просмотров: 114; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!