Задачи для самостоятельного решения.
Решить тест. (тест будет открыт до среды, 2 попытки)
1. Переписать все в тетрадь (и теорию и полностью разобранные примеры).
2. Решить задачи для самостоятельного решения и прислать фото с решенными задачами до 8.02. на почту sneshanasmirnova@yandex.ru
Применение производной для исследования функций.
Понятие производной – одно из важнейших в математике. С помощью производной можно решать самые разнообразные задачи, относящиеся к любой области человеческой деятельности. В частности, с помощью производных стало возможным подробное исследование функций, что позволило очень точно строить их графики, находить их наибольшие и наименьшие значения и т. д.
Промежутки монотонности функции
Функция y=f(x) называется возрастающей в некотором интервале, если в точках этого интервала большему значению аргумента соответствует большее значение функции, и убывающей, если большему значению аргумента соответствует меньшее значение функции.
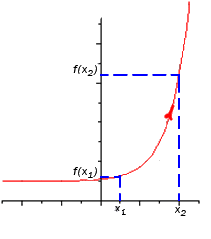
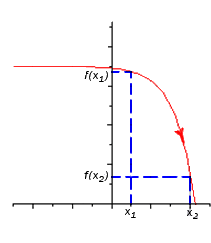
Промежутки возрастания и убывания функции называются промежутками ее монотонности
Теорема. Если производная функции y=f(x) положительна (отрицательна) на некотором интервале, то функция в этом интервале монотонно возрастает (монотонно убывает).
Алгоритм нахождения промежутков монотонности функции:
1. Находим область определения функции f(x).
2. Вычисляем производную f'(x) данной функции.
|
|
|
3. Находим точки, в которых производная f'(x)= 0 или не существует. Эти точки называются критическими для функции f(x).
4. Делим область определения функции этими точками на интервалы. Они являются интервалами монотонности.
5. Исследуем знак производной функции на каждом интервале. Если f'(x)>0, то на этом интервале f(x) возрастает; если f'(x)<0, то на таком интервале функция f(x) убывает.
Рассмотрим теперь нахождение промежутков возрастания/убывания на конкретном примере функции.
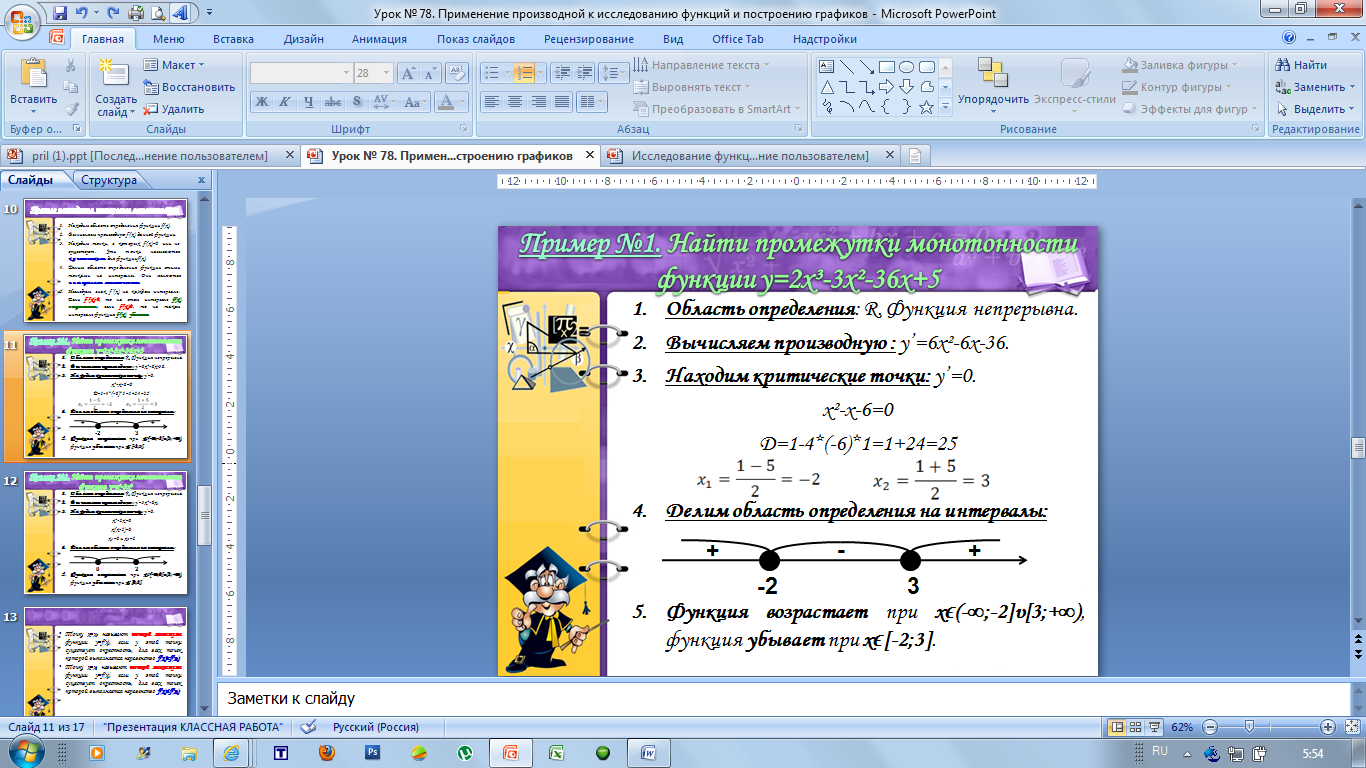
Пример №1. Найти промежутки монотонности функции y=2x³-3x²-36x+5.
1. Область определения: R.
2. Вычисляем производную: y'=(2x3-3x2-36x+5)'=6x²-6x-36.
3. Находим критические точки: y'=0.
6x²-6x-36=0
x²-x-6=0
Д=1-4*(-6)*1=1+24=25
x1=-2, x2=3
4. Делим область определения на интервалы: (-∞;-2],[-2;3] и [3;+∞),
5. Исследуем знак производной на каждом интервале.
x=-3 є (-∞;-2] y'(-3)=6*(-3)2-6*(-3)-36=18>0
x=0 є [-2;3] y'(0)=6*02-6*0-36=-36<0
x=4 є [3;+∞), y'(4)=6*42-6*4-36=36>0
Отмечаем все на следующей схеме:
| y' |
| y |
Функция возрастает при xϵ(-∞;-2] U [3;+∞) (, функция убывает при xϵ[-2;3].
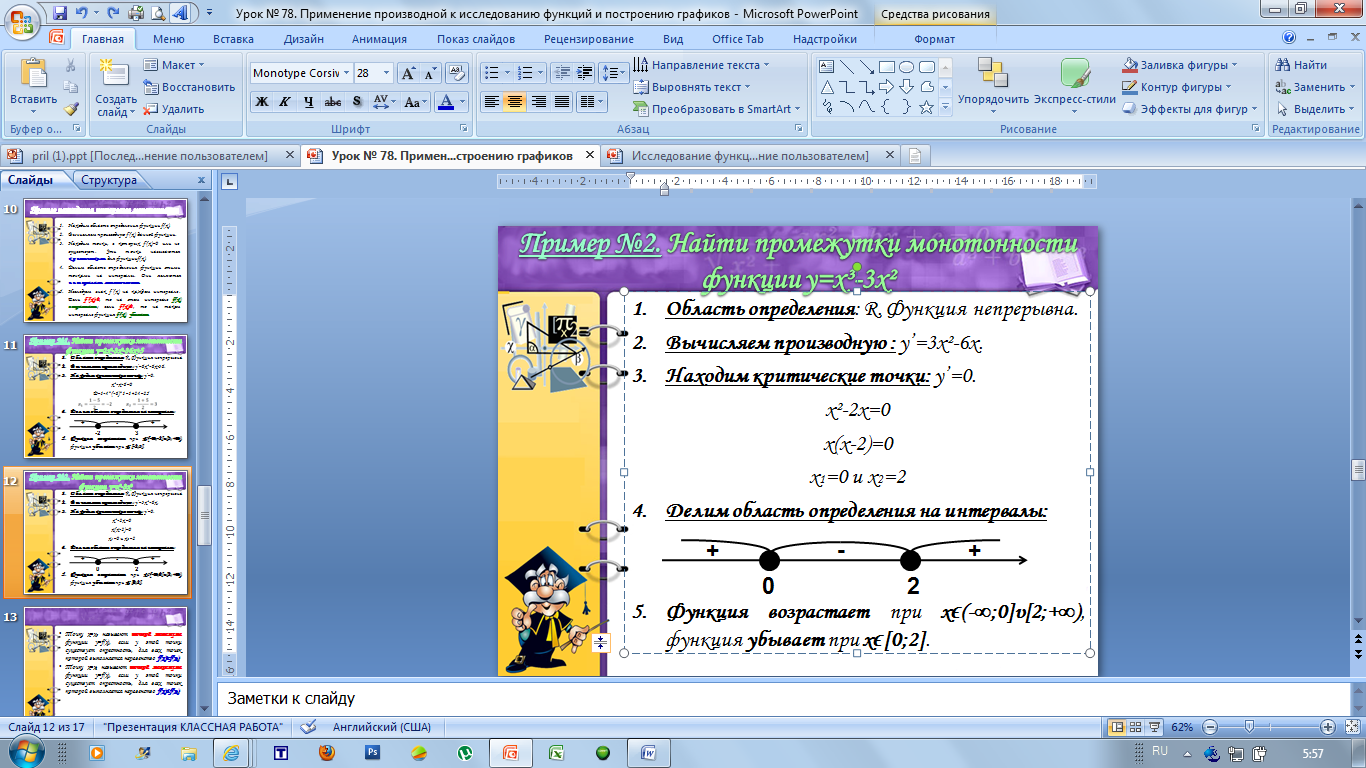
Пример №2. Найти промежутки монотонности функции y=x³-3x².
1. Область определения: R.
2. Вычисляем производную: y'=(x3-3x2)'=3x²-6x.
|
|
|
3. Находим критические точки: y'=0.
y'=3x2-6x=0
x²-2x=0
x(x-2)=0
x1=0 и x2=2
4. Делим область определения на интервалы: (-∞;0], [0;2] и [2;+∞),
5. Исследуем знак производной на каждом интервале.
x=-1 є (-∞;0] y'(-1)=3*(-1)2-6*(-1)=9>0
x=1 є [0;2] y'(1)=3*12-6*1=-3<0
x=4 є [2;+∞) y'(4)=3*42-6*4=24>0
Отмечаем все на следующей схеме:
| y' |
| y |
Функция возрастает при xϵ(-∞;0] U [2;+∞), функция убывает при xϵ[0;2].
Пример №3. Найти промежутки монотонности функции y=2x2-lnx
1. Область определения: x>0, т.к. значение под знаком логарифма может быть только положительным.
2. Вычисляем производную: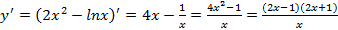 
3. Находим критические точки: y'=0.
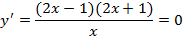
(2x-1)(2x+1)=0
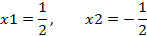
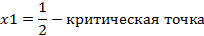
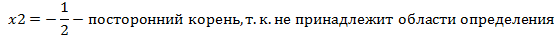
4. Делим область определения на интервалы: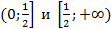 
5. Исследуем знак производной на каждом интервале.
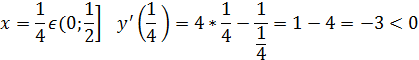
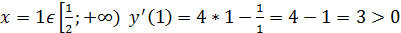
Отмечаем все на следующей схеме:
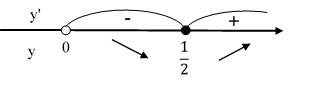
Функция возрастает при xϵ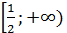 
и функция убывает при xϵ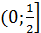 
Задачи для самостоятельного решения.
Найти промежутки монотонности следующих функций:
1) 
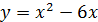
2) 
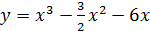
3) 
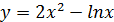
Дата добавления: 2022-06-11; просмотров: 16; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!