Порядок выполнения упражнения
ИЗУЧЕНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Цель работы: экспериментальное исследование электростатического поля методом электростатической ванны и описание его при помощи силовых линий и поверхностей равного потенциала.
Принадлежности: специальная установка, набор сменных электродов
2.1. Теоретические сведения
2.1.1. Закон Кулона. Напряженность электрического поля
Взаимодействие точечных зарядов q1и q2 описывает экспериментальный закон Кулона:
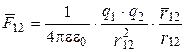 , (2.1)
, (2.1)
где 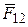 - сила, действующая на q1 со стороны q2;
- сила, действующая на q1 со стороны q2;
r12 - расстояние между зарядами;
 - единичный вектор направленный от q2 к q1;
- единичный вектор направленный от q2 к q1;
eо - диэлектрическая постоянная, определяемая из опыта;
e - диэлектрическая проницаемость среды (для вакуума e=1, для диэлектриков e>1).
Опыт показывает, что при наличии зарядов q1, q2, q3,..., результирующая сила 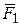 , действующая со стороны поля на заряд q1, равна векторной сумме сил
, действующая со стороны поля на заряд q1, равна векторной сумме сил 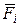 , приложенных к нему со стороны каждого из зарядов qi:
, приложенных к нему со стороны каждого из зарядов qi:
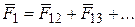 , (2.2)
, (2.2)
где 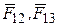 ,... определяются по закону Кулона (2.1).
,... определяются по закону Кулона (2.1).
Напряженность электрического поля в данной точке есть векторная величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:
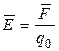 , (2.3)
, (2.3)
где  - сила, действующая на пробный заряд qо, помещенный в рассматриваемую точку пространства. В частности, напряженность поля точечного заряда q определяется в соответствии с законом Кулона (2.1) по формуле:
- сила, действующая на пробный заряд qо, помещенный в рассматриваемую точку пространства. В частности, напряженность поля точечного заряда q определяется в соответствии с законом Кулона (2.1) по формуле:
|
|
|
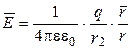 , (2.4)
, (2.4)
где  - вектор, проведенный от точечного заряда q в данную точку.
- вектор, проведенный от точечного заряда q в данную точку.
Поле, создаваемое неподвижными относительно выбранной системы отсчета зарядами, называется электростатическим.
Если поле создается точечными зарядами q1, q2,..., то согласно выражению (2.2) имеет место принцип суперпозиции полей:
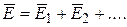 , (2.5)
, (2.5)
где 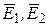 ,... - напряженность полей, создаваемых в данной точке каждым из зарядов q1, q2,... в отдельности, а Е - суммарная напряженность результирующего поля.
,... - напряженность полей, создаваемых в данной точке каждым из зарядов q1, q2,... в отдельности, а Е - суммарная напряженность результирующего поля.
2.1.2. Работа в электростатическом поле. Потенциал
На заряд qо в электростатическом поле Е действует сила F = qоЕ, и, следовательно, при его перемещении совершается работа. Рассмотрим электростатическое поле, создаваемое точечным зарядом q, и найдем работу, совершаемую (силами поля) при перемещении заряда qо из точки 1 в точку 2 (рис.2.1). Для определенности возьмем заряды q и qо одного знака. На элементарном участке пути dl совершается работа
|
|
|
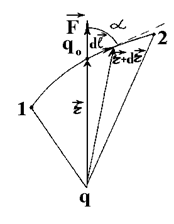 Рис.2.1
Рис.2.1
|  и и 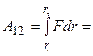
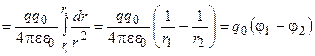 , (2.6)
где потенциал φ в точке электростатического поля определяется точечным зарядом q и расстоянием r от него до точки: , (2.6)
где потенциал φ в точке электростатического поля определяется точечным зарядом q и расстоянием r от него до точки:
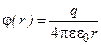 (2.7) (2.7)
|
Таким образом, работа по перемещению заряда qо в поле неподвижного точечного заряда q не зависит от выбора траектории и определяется только его начальным и конечным положением. В частности, работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому контуру L, равна нулю, т.е.

Так как qо ≠ 0, то 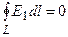 . (2.8)
. (2.8)
Величину 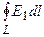 называют циркуляцией вектора Е по замкнутому контуру L . Согласно формуле (2.8) для электростатического (!) поля точечного заряда характерным является то, что в нем циркуляция Е по любому замкнутому контуру равна нулю (электростатическое поле потенциальное, а электростатические силы консервативные).
называют циркуляцией вектора Е по замкнутому контуру L . Согласно формуле (2.8) для электростатического (!) поля точечного заряда характерным является то, что в нем циркуляция Е по любому замкнутому контуру равна нулю (электростатическое поле потенциальное, а электростатические силы консервативные).
Как известно, работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу А12 можно представить как разность потенциальных энергий, которыми обладает заряд qо в начальной и конечной точках поля заряда q:
А12 = W1 - W2. (2.9)
|
|
|
Принято говорить просто об энергии заряда qо в электростатическом поле. Сравнивая выражения (2.9) и (2.6), получаем
φ(r) = W/qо. (2.10)
В силу принципа суперпозиции формулы (2.8) - (2.10) остаются справедливыми и в случае, когда электростатическое поле создается зарядами q1, q2,... . При этом Е = E1+ E2+ ... и φ =φ1+ φ2+ ... в каждой точке.
Величину φ называют потенциалом поля в данной точке. Согласно выражению (2.10) потенциал в точке электростатического поля равен потенциальной энергии, которую имел бы единичный положительный заряд, помещенный в эту точку . В частности, потенциал поля точечного заряда определяется формулой (2.7). Из выражения (2.10) получаем единицу потенциала : 1В = 1Дж /1Кл. Для разности потенциалов в точках 1 и 2 имеем:
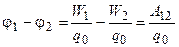 (2.11)
(2.11)
Таким образом, разность потенциалов в двух точках равна работе, совершаемой полем при перемещении единичного положительного заряда из начальной точки в конечную.
Работа сил поля при перемещении заряда qо из точки 1 в точку 2 может быть записана также в виде
 (2.12)
(2.12)
Из формул (2.11) и (2.12) вытекает выражение для разности потенциалов:
|
|
|
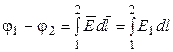 , (2.13)
, (2.13)
где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки.
2.1.3. Связь между напряженностью Е и потенциалом j
Рассмотрим произвольное направление  (рис.2.2). Из выражения (2.13)
(рис.2.2). Из выражения (2.13)
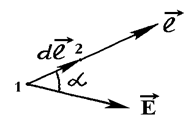
 Рис.2.2 Рис.2.2
| при условии, что точки 1 и 2 рас- j положены бесконечно близко друг к другу, имеем:
j1-j2 = -(j2-j1) = -dj = Еdlcos a = Еldl
или 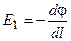 (2.14)
Отсюда часто используемая единица измерения - В/м. (2.14)
Отсюда часто используемая единица измерения - В/м.
|
В частности, 
Вектор с проекциями  на оси x, y, z соответственно называют градиентом скалярной функции j (x,y,z) и обозначают gradj.
на оси x, y, z соответственно называют градиентом скалярной функции j (x,y,z) и обозначают gradj.
Таким образом, 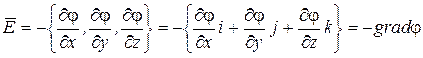 (2.15)
(2.15)
Пусть точка О - любая (фиксированная) точка поля, а М - произвольная точка сферы бесконечно малого радиуса ρ с центром в точке О(рис.2.3). По определению разности потенциалов,
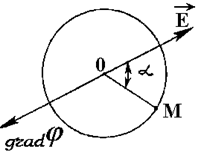 Рис.2.3
Рис.2.3
| φ(O) - φ(M) ≡ Е(O)ρ cosα. (2.16) Эта разность, очевидно, максимальна при α1= 0, то есть при перемещении из точки О вдоль вектора напряженности Е, и мини- Рис.2.3 мальна при α2= π, то есть при перемещении из точки О вдоль вектора -Е = grad φ. Таким образом, gradφ направлен в сторону максимального роста, а вектор напряженности Е |
- в сторону максимального убывания потенциала φ(x,y,z).
Для графического изображения полей пользуются силовыми линиями. Силовая линия проводится так, что касательная к ней в каждой точке совпадает с прямой, вдоль которой направлен вектор напряженности Е в этой точке. Этим линиям приписывают направление, совпадающее с направлением вектора напряженности Е.
Плотность силовых линий, то есть число силовых линий, пронизывающих площадку в 1 м2, расположенную перпендикулярно к ним, выбирают равной величине Е. Таким образом, с помощью силовых линий можно графически изобразить и величину, и направление вектора напряженности Е.
Эквипотенциальной называют поверхность, все точки которой имеют одинаковый потенциал φ(x,y,z) = const. Очевидно, в каждой точке такой поверхности вектор Е перпендикулярен к этой поверхности (рис.2.4), следовательно, силовые линии ортогональны к эквипотенциальным поверхностям.
Эквипотенциальные поверхности обычно строят так, чтобы разности потенциалов между любыми двумя соседними поверхностями были одинаковыми (рис.2.5). Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности расположены гуще, напряженность поля больше.
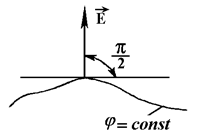 Рис.2.4
Рис.2.4
|  Рис.2.5
Рис.2.5
|
Зная расположение эквипотенциальных поверхностей, можно построить силовые линии и найти значения напряженности поля.
2.2. Описание установки и метод измерения
Исследование электростатического поля заключается в нахождении вектора напряженности Е в каждой его точке. Аналитический расчет полей возможен лишь для заряженных тел простой формы (сфера, цилиндр и т.п.). При
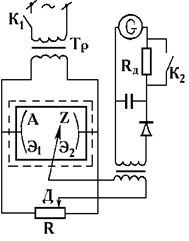 Рис.2.6
Рис.2.6
| сложных поверхностях тел (электродов) такой расчет затруднителен, и тогда электростатическое поле исследуют экспериментально. Для этого сначала определяют положение и форму эквипотенциальных поверхностей, а затем (перпендикулярно к ним) проводят силовые линии. Построение эквипотенциальных поверхностей в полях различной конфигурации производится в данной работе с помощью установки для исследования межэлектродных статистических полей типа ФН9, схематически изображенной на рис.2.6 (упрощенная схема). |
В прямоугольную электролитическую ванну А, заполненную раствором слабого электролита, помещаются металлические электроды Э1 и Э2, поле которых изучается. На зажимы электродов подается переменное напряжение от силового трансформатора Тр.
Между электродами возникает упорядоченное движение зарядов (ионов). При этом плотность тока, согласно закону Ома в дифференциальной форме, в каждой точке электролита пропорциональна вектору напряженности Е в данной точке:
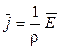 (2.17)
(2.17)
где ρ - удельное сопротивление электролита.
Таким образом, картина линий тока в электролите будет аналогична картине силовых линий Е.
Указанный метод исследования поля называется моделированием. На практике вместо постоянного тока используется переменный ток небольшой частоты, чтобы исключить искажения поля за счет поляризации среды, возникающей в результате электролиза раствора солей.
В измерительную схему входят зонд Z, делитель напряжения R, нулевой гальванометр G с добавочным сопротивлением R9 и тумблером K2.
Зонд Z представляет собой тонкий металлический стержень, хорошо изолированный по всей длине, кроме конца. Измерительная схема работает по следующему принципу: перемещением движка Д на делителе напряжения можно придавать различные значения потенциала (в пределах полной разности потенциалов) этому движку относительно электродов, погруженный в ванну . В какой-нибудь точке поля устанавливается зонд Z. Если зонд находится в такой точке поля, потенциал которой равен потенциалу движка делителя, то не будет тока в цепях зонда и, следовательно, гальванометра. Геометрическое место точек поля, для которых стрелка гальванометра займет нулевое положение при данном положении движка делителя, будет соответствовать одной из эквипотенциальных поверхностей исследуемого поля. Из-за малой глубины ванны в опыте получается не поверхность, а её горизонтальное сечение - линия.
Перемещая движок на делителе напряжения, придают движку различные значения потенциала и для каждого такого значения находят соответствующую эквипотенциальную линию (перемещая зонд в ванне). Фиксирование положения и формы эквипотенциальных линий электростатического поля, получаемых с помощью зонда, производится графически с применением пантографа (рис.2.7).
 Рис.2.7
Рис.2.7
| К концу направляющей линейки 1 пантографа прикрепляется зонд Z, перемещающийся вместе с линейками в горизонтальной плоскости над ванной. Нижний конец зонда помещен в i электролит, а верхний через первичную обмотку трансформатора гальванометра соединен с движком двигателя напряжения R (см.рис.2.6). Зондом можно обсле- |
довать всю ванну.
Для фиксирования эквипотенциальных линий на листе бумаги, закрепленном на подставке, служит правая часть пантографа. К концу направляющей линейки 2 прикреплен карандаш К. Карандаш может перемещаться вместе с линейкой над листом бумаги, не касаясь её. Прикосновение карандаша к бумаге осуществляется при нажиме на него. Система направляющих линеек устроена так, что любому горизонтальному перемещению зонда в ванне автоматически соответствует перемещению карандаша над листом бумаги.
Найденные с помощью зонда точки, принадлежащие исследуемой эквипотенциальной линии, фиксируются с помощью карандаша на листе бумаги и соединяются плавной кривой.
2.3. Порядок выполнение работы
1. Установить в ванне и закрепить зажимами систему из двух электродов, образующих плоский конденсат.
2. Вложить лист бумаги в крепление подставки пантографа.
3. Обвести зондом контуры поверхностей электродов и получить на листе бумаги соответствующие им эквипотенциальные линии.
4. Тумблер К2 установить в положение "грубо".
5. Включить питание установки, замыкая ключ К1, и зафиксировать положение движка Д.
6. Поместить зонд вблизи одного из электродов.
7. Перемещением движка делителя добиться нулевого положения стрелки гальванометра, только после этого перевести тумблер К2 в положение "точно" (гальванометр при этом приобретает большую чувствительность за счет отключения добавочного сопротивления). Точнее найти положение движка делителя, соответствующее нулевому току гальванометра.
8. Переместить зонд так, чтобы стрелка гальванометра по-прежнему показывала нуль, На листе бумаги зафиксировать не менее 10 точек, принадлежащих исследуемой эквипотенциальной линии.
9. Соединить плавной кривой найденные точки и получить эквипотенциальную линию.
10. Построить четыре эквипотенциальных линии, пользуясь указаниями пунктов 7...9 и помещая зонд на другие точки поля так, чтобы разности потенциалов между двумя соседними линиями были одинаковыми (φ2- φ1= φ3- φ2= φ4- φ3).
11. Установить в ванне новые системы электродов и повторить операции, указанные в пунктах 2...10.
12. Каждое поле построить на отдельном листе, изображая как эквипотенциальные линии, так и построенные ортогонально им силовые линии.
13. На оси симметрии системы электродов (в области поля, где Еx ≠ 0, Еy=0, Еz=0) определить поведение напряженности. Для этого оценить величину напряженности Еx= ∆φ/∆x (В/мм) электрического поля, определив ∆φ - разность потенциалов между соседними эквипотенциальными линиями, ∆x - расстояние между этими линиями вдоль оси симметрии.
14. Оценить точность выполнения измерений.
2.4. Контрольные вопросы
1. Как определяются напряженность и потенциал электростатического поля? Назовите единицы измерения 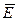 и φ.
и φ.
2. Приведите графики зависимостей Е(r) и φ(r) для точечного заряда.
3. Какая связь существует между 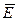 и φ в общем случае и в случае однородного поля?
и φ в общем случае и в случае однородного поля?
4. Как определяются силовые линии и эквипотенциальные поверхности?
5. Какова взаимная ориентация поверхностей равного потенциала и линий напряженности в электрическом поле? Докажите такую ориентацию?
6. Что называется циркуляцией вектора напряженности? Как доказать, что электростатическое поле является потенциальным?
7. Как моделируется и исследуется электростатическое поле в данной работе ?
Литература. [1 §§ 1 - 12; 2 §§ 1- 8; 4 §§ 1, 2, 8] .
ИЗУЧЕНИЕ ЯВЛЕНИЯ ДИФРАКЦИИ
Целью настоящей работы является ознакомление с явлением дифракции и экспериментальное определение длины световой волны при помощи дифракционной решетки.
2.1.Теоретическое введение
Дифракцией света называется явление отклонения световых лучей от прямолинейного направления при ограничении световых пучков какими-либо преградами (узкие отверстия, щели, резкие края препятствий). Явление дифракции можно представить как огибание световыми волнами преград, стоящих на их пути. Масштаб огибания зависит от отношения размеров преграды к длине волны.
Дифракция легко наблюдается, если размеры преграды, например, щели, через которую проходит свет, соизмеримы с длиной волны в пределах нескольких порядков.
В зависимости от схемы наблюдения дифракционные явления условно разделяют на дифракцию Френеля и дифракцию Фраунгофера.
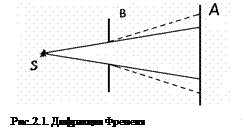
Дифракция Френеля наблюдается в расходящихся пучках лучей, когда на пути фронта световой волны располагается лишь непрозрачный экран B, частично загораживающий этот фронт (рис.2.1). Дифракционная картина наблюдается на другом экране A, параллельном экрану В.
 В случае дифракции монохроматического света на небольшом круглом отверстии в непрозрачном экране дифракционная картина имеет вид чередующихся светлых и темных концентрических колец.
В случае дифракции монохроматического света на небольшом круглом отверстии в непрозрачном экране дифракционная картина имеет вид чередующихся светлых и темных концентрических колец.
Дифракция Фраунгофера наблюдается в параллельных лучах. Чтобы этот тип дифракции осуществить, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием (рис.2.2).
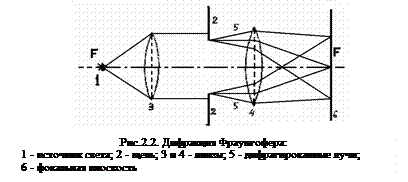
В случае дифракции монохроматического света на узкой длинной щели в непрозрачном экране дифракционная картина представляет собой чередование темных и светлых полос, симметрично расположенных по обе стороны от центральной светлой полосы.
Дифракция обнаруживает волновые свойства света и может быть объяснена с помощью принципа Гюйгенса-Френеля, согласно которому волновое возмущение в любой точке пространства можно рассматривать как результат интерференции когерентных вторичных волн от фиктивных источников, на которые можно разбить волновую поверхность световой волны, распространяющейся от реального источника. Френель предложил разбивать волновую поверхность на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки наблюдения отличаются на λ/2 (λ - длина волны в той среде, в которой распространяется волна). Обладающие таким свойством зоны носят название зон Френеля (рис.2.3).
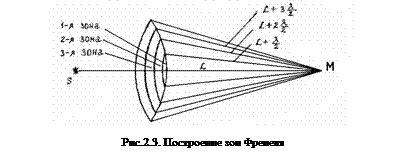
Колебания, возбуждаемые в точке М двумя соседними зонами, противоположны по фазе, т.к. разность хода от сходственных точек этих зон до точки М равна λ/2. Поэтому при наложении эти колебания будут взаимно ослаблять друг друга, а амплитуда A результирующего светового колебания в точке М может быть представлена в виде:
А=А1-А2+А3-А4+... ,
где A - амплитуда колебаний, возбуждаемых i-й зоной. Значение Ai зависит от площади i-й зоны и от угла между нормалью к поверхности зоны и направлением на точку М.
2.1.1. Дифракция на щели
Рассмотрим дифракцию Фраунгофера на щели. Пусть монохроматический свет от источника 1 (рис.2.4) освещает щель 2, находящуюся в фокальной плоскости линзы 3. Выйдя из линзы, параллельный пучок лучей падает на щель ВС, расположенную перпендикулярно плоскости рисунка. Ширина щели равна а.
Каждая точка волнового фронта, достигшего щели, согласно принципу Гюйгенса-Френеля, является источником вторичных сферических волн, вследствие чего лучи от щели пойдут не только в первоначальном направлении, но и под различными углами φ к этому направлению. Эти лучи называются дифрагированными , а угол φ - углом дифракции.

Если ширина щели соизмерима с длиной волны λ монохроматического света от источника 1, то на экране 6, помещенном в фокальной плоскости линзы 5, наблюдается дифракционная картина.
Найдем освещенность в точке P экрана, в которой соберутся лучи, дифрагированные под углом φ. Для этого разобьем открытую часть волновой поверхности в плоскости щели ВС на зоны Френеля, имеющие вид полос, параллельных краям щели. Всего на ширине щели уместится Δ/( λ/2) зон, где Δ - разность хода между крайними лучами ВМР и CNP. Из треугольника BCD имеем:
Δ = BD =а• sin φ, (2.2)
где D - основание перпендикуляра, опущенного из точки C на луч ВМ (СД - фронт волны, дифрагированной под углом φ).
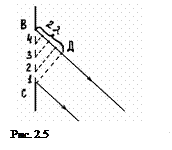 Если, например, Δ = 2 λ, то Δ/( λ/2) =4, т.е. 0 число зон Френеля равно 4 (рис. 2.5). Все зоны излучают свет в рассматриваемом направлении совершенно одинаково, причем колебания, возбуждаемые в точке P двумя соседними зонами, равны по амплитуде и противоположны по фазе.
Если, например, Δ = 2 λ, то Δ/( λ/2) =4, т.е. 0 число зон Френеля равно 4 (рис. 2.5). Все зоны излучают свет в рассматриваемом направлении совершенно одинаково, причем колебания, возбуждаемые в точке P двумя соседними зонами, равны по амплитуде и противоположны по фазе.
Из выражения (2.2) вытекает, что число зон Френеля, укладывающихся на ширине щели, зависит от угла φ. Если угол φ таков, что разность хода между крайними лучами пучка равна четному числу полуволн (что соответствует четному числу зон Френеля), то на экране будет наблюдаться дифракционный минимум, так как колебания от каждой пары соседних зон взаимно погашают друг друга. Если же угол φ таков, что разность хода между крайними лучами пучка равна нечетному числу полуволн (что соответствует нечетному числу зон Френеля), то будет наблюдаться дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля.
Таким образом, при дифракции от одной щели положение максимумов определяется условием:
а• sin φ = ±(2k+1) λ/2, где k=1,2,3,... . (2.3)
Для минимумов:
а• sin φ = ±2k ( λ/2), где k=1,2,3.... . (2.4)
При φ =0 все лучи, проходящие через щель, соберутся в главном фокусе линзы F. Разность хода между всеми этими лучами равна нулю, поэтому произойдет их взаимное усиление, и в точке F будет наблюдаться самый яркий центральный максимум.
С ростом k ширина зон Френеля и интенсивность максимумов быстро уменьшается. Распределение интенсивности света на экране для монохроматического света приведено на рис.2.6.
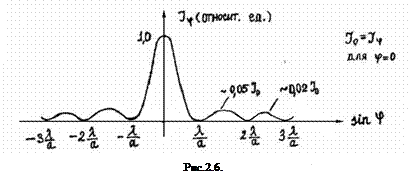
2.1.2. Дифракция на дифракционной решетке
Одномерная дифракционная решетка представляет собой систему из большого числа одинаковых параллельных щелей, разделенных также одинаковыми непрозрачными промежутками. Если а и в - соответственно ширина прозрачного и непрозрачного промежутков, то величина d = а + b называется постоянной решетки или ее периодом.
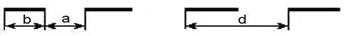
 Дифракционные решетки изготовляют методом нанесения тонких штрихов (царапин) на поверхность стеклянной пластинки (прозрачная решетка) или металлического зеркала (отражательная решетка).
Дифракционные решетки изготовляют методом нанесения тонких штрихов (царапин) на поверхность стеклянной пластинки (прозрачная решетка) или металлического зеркала (отражательная решетка).
Дифракционной решеткой может служить совокупность большого числа любых неоднородностей (отверстий и преград) на плоскости или в объеме; в последнем случае решетка называется пространственной. Например, трехмерную пространственную решетку представляют собой кристаллы твердых тел.
Схема наблюдения дифракции на прозрачной решетке представлена на рис.2.7.
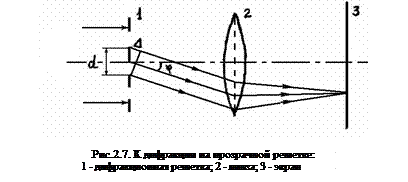
На дифракционную решетку падает пучок параллельных лучей перпендикулярно к плоскости, в которой лежат щели. Решетка 1 вызывает дифракцию световых лучей, и на экране 3, помещенном в фокальной плоскости линзы 2, образуется дифракционная картина. Явлению дифракции сопутствует явление интерференции - наложение когерентных дифрагированных волн друг на друга.
Каждая щель решетки дает дифракционную картину в соответствии c уже описанной. При этом дифракционные максимумы и минимумы налагаются друг на друга. Однако основные черты общей дифракционной картины определяются как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света.
Выберем пучки от каждой щели решетки, распространяющиеся под одинаковым углом φ к нормали к дифракционной решетке. Собранные линзой 3 в одну линию (проходящую через точку P экрана), эти лучи проинтерферируют. Если общее число щелей в решетке N, то и интерферируют между собой N пучков. Результат интерференции будет зависеть от разности хода Δ между пучками. Так как щели находятся друг от друга на одинаковых расстояниях, то и разности хода лучей, идущих от двух соседних щелей, будут для данного направления φ одинаковы в пределах всей решетки:
Δ = (a + b) sin φ = d sin φ . (2.5)
Этой разности хода соответствует разность фаз
δ =2π•(Δ/λ)=2π•( d • sin φ)/λ. (2.6)
Если
δ = ±2 πk, (2.7)
то колебания от всех щелей придут в точку P в одинаковой фазе, и будут взаимно усиливать друг друга. Амплитуда колебаний в этой точке равна:
Amax = NA, (2.8)
где A - амплитуда колебания, посылаемого одной щелью под углом φ.
Из соотношений (2.6) и (2.7) получим условие максимумов интенсивности:
d•sin φ = ±k λ , где k=0, 1, 2 ... (2.9)
Максимумы, определяемые данным условием, называются главными. Число k дает порядок главного максимума. Центральный максимум представляет собой максимум нулевого порядка. По обе стороны от него располагаются максимумы 1-го, 2-го и т.д. порядков.
Интенсивность главных максимумов Jmax в N2 раз больше интенсивности Jф, создаваемой в направлении φ одной щелью. Действительно, возведя равенство (2.8) в квадрат, получим:
Jmax=N2Jф. (2.10)
Главные минимумы при дифракции света на дифракционной решетке наблюдаются под углами дифракции φ, соответствующими минимумам при дифракции на одной щели:
а• sin φ= ± kλ, где k=1, 2, 3... (2.11)
В этих направлениях каждая из щелей не дает света (сама себя гасит).
Более детальный анализ многолучевой интерференции в дифракционной решетке показывает, что в промежутках между соседними главными максимумами имеется N-1 дополнительных минимумов и соответственно N-2 вторичных максимумов, интенсивность которых пренебрежимо мала по сравнению с главными максимумами.
В монохроматическом свете дифракционная картина имеет вид узких и ярких главных максимумов, разделенных практически темными широкими промежутками. Таким образом, световая энергия, падающая на решетку, перераспределяется ею так, что большая ее часть приходится на максимумы, а в минимумы попадает незначительная часть энергии. При увеличении числа щелей яркость главных максимумов возрастает, а вторичных уменьшается.

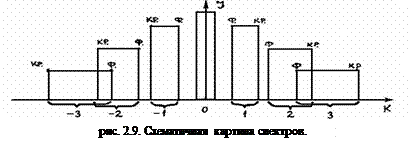
При освещении решетки белым светом условия максимума (2.9) и минимума (2.11) будут справедливы для всех длин волн, и дифракционный спектр будет в виде окрашенных максимумов для λ1, λ2, λ3, ... Как видно из формулы (2.9), в центре (φ=0) будет белая полоса, максимум нулевого порядка для λ1, λ2, λ3, ... . По обе стороны от нулевого будут располагаться максимумы 1, 2, ... порядков для λ1, λ2, ... . Эти максимумы, сливаясь друг с другом, образуют окрашенные полосы - спектры 1, 2, ... порядков. Причем, чем короче длина волны, тем ближе расположен максимум к центральному, что видно из d• sin φ= ± kλ. При k=1 возникнут два спектра первого порядка (правый и левый), расположенных фиолетовыми концами к центральной белой полосе (λфиол.< λкрасн.). При k=2, 3, ... аналогично, спектры второго, третьего и т.д. порядков (рис. 2.9.).
2.2. Выполнение работы.
Упражнение 1. Определение длины световой волны при помощи дифракционной решетки.
Приборы и принадлежности: источник света - лампа накаливания, оптическая скамья со шкалой, дифракционная решетка.


Длина волны определяется из условия главного максимума:
d• sin φ= k λ,
откуда λ=( d/ k)• sin φ. Так как из треугольника всо: sin φ ≈ l/Д и так как φ мало, то:
λ = ( d/ k)•( l/Д). (2.12)
Порядок выполнения упражнения
1. Внимательно ознакомиться с теорией дифракционной решетки по описанию.
2. Включить источник света - лампу.
3. Передвигая шкалу АВ (рис.2.11) вдоль оптической скамьи, установить ее на расстоянии Д от дифракционной решетки РР' так, чтобы линии дифракционной картины были хорошо видны.
4. Просмотреть дифракционную картину, убедиться, что она симметрична, состоит из спектров 1, 2, ... порядка (не меньше). Для белого света спектры 1,2 порядков состоят из цветных полос. Спектр нулевого порядка - белый.
5. Измерить расстояние l в мм от нуля шкалы (φ=0) до середины той цветной линии в спектре 1 порядка, длину волны которой надо определить. Отсчет l делают справа и слева от нуля и находят lср.=( lпр .+ lлев.)/2 для данной λ.
6. Записать в таблицу измерений 2.1 значения l, Д, d, k и по формуле (2.12) λ = ( d/ k)•( l/Д) определить длину волны λ в мм, а затем перевести в ангстремы (1мм=107 А).
7. То же самое сделать для других линий, указанных преподавателем, в спектре 1, 2 порядка при Д1, затем для Д2.
8. Определить относительную и абсолютную погрешности для линии одного цвета в спектре первого порядка k=1 по формулам:
δ= Δλ/ λ= ( δd/ d) + ( δl/ l) + ( δД/Д); Δλ= ( λ• δ) Å.
9. Вычислить для линий одного цвета во всех порядках (k) и для всех значений Д величину λср.=( λ1+ λ2+ λ3+...+ λ k)/ n, где n - число измерений.
10. Записать результат измерения: λср.± Δλ=...
Таблица 2.1
| Цвет линии | Д, мм | d , мм | k | l , мм | l ср , мм | sin φ = l ср /Д | λ , Å | λср , Å | |
| Пр. | Лев. | ||||||||
| Красная Зеленая Фиолетовая | Д1= x |
| |||||||
| Красная Зеленая Фиолетовая | Д2= y |
| |||||||
Упражнение 2. Определение дисперсии и разрешающей силы дифракционной решетки.
Дифракционная решетка - спектральный прибор, спектр которого характеризуется угловой дисперсией и разрешающей силой. Дисперсия и разрешающая сила - спектральные характеристики решетки, определяющие качество спектра, т.е. ширину его линий и расстояние между ними. Дисперсия характеризует способность дифракционной решетки пространственно разделять пучки лучей различных длин волн и определяет протяженность спектра.
Угловая дисперсия (Д') определяется угловым расстоянием между двумя спектральными линиями, отличающимися по длине волны на Δλ=1Å. Мерой угловой дисперсии является отношение Δφ/ Δλ ("/A), где (") - угловая секунда. Выражение для угловой дисперсии можно получить, продифференцировав формулу d• sin φ= k λ, где d, k- постоянные, φ, λ - переменные:
 ,
,
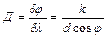 .
.
Разрешающая сила (r) характеризует способность дифракционной решетки разделять (разрешать) спектральные линии, мало отличающиеся по длинам волн. За меру разрешающей силы принимается отношение λ/ δλ, где λ и δλ связаны условием: δλ= λ1- λ. Здесь λ1 и λ соответствуют двум соседним линиям, которые разрешаются решеткой.
При расчете разрешающей силы решетки следует исходить из условия Рэлея различимости двух световых пятен. По Релею: две близкие спектральные линии считаются разрешенными, если максимум одной из них совпадает с первым минимумом другой (ближайшим из N-1 минимумов).
Тогда теория дает для разрешающей силы дифракционной решетки следующее выражение:
r= λ/ δλ =К•N, (2.14)
где K - порядок спектра, N - полное число действующих штрихов решетки.
В данной работе предлагается графический метод определения угловой дисперсии для спектра 1 порядка.
2.3. Контрольные вопросы
1. Явление дифракции. При каком условии оно наблюдается?
2. Сформулируйте принцип Гюйгенса-Френеля.
3. Какие волны называются когерентными?
4. В чем заключается метод зон Френеля?
5. Запишите условия минимума и максимума при дифракции на щели и поясните их.
6. Докажите, что разность хода между соседними лучами, идущими от правых краев каждой щели дифракционной решетки, равна Δ = d • sinφ .
7. Каков порядок следования цветов в дифракционных спектрах? Какова окраска нулевого максимума?
8. Интерференционная картина представляет собой чередование минимумов и максимумов. Почему через дифракционную решетку мы видим цветную картину?
9. Какова область видимого света по длине волн и частоте?
Литература
[1], §§ 125-130;
[2], §§ 32.1-32.4;
[3], §§ 177, 178, 180, 181;
[4], ч. II, гл. VII, §§ 54-55;
[5], §§ 33, 39, 40, 44, 46;
[6], стр. 264-268.
Дата добавления: 2022-06-11; просмотров: 23; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
