Динамические характеристики апериодического (инерционного) звена

Идеальное дифференцирующее звено и его динамические характеристики.

Идеальным дифференцирующим звеном называется такое звено, движение которого описывается дифференциальным уравнением 1-го порядка вида

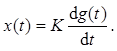
Передаточная функция W(s):

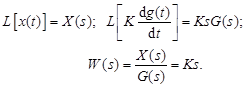(2.66)

Переходная функция (табл. 2.6)

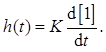
Известно, что производная от единичной функции есть δ-функция, тогда

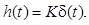
Весовая функция

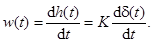
Это производная от δ-функции, которая представляет графически бесконечный всплеск в нуле в обе стороны по оси ординат (см. табл. 2.6).

КЧХ звена W(jω)=jωK. Это прямая, выходящая из начала координат при ω=0 и идущая по оси ординат в ∞ (см. табл. 2.6). Такое ее расположение связано с тем, что вещественная частотная характеристика U(ω) равна 0 при всех ω, т.е. ВЧХ представляет прямую, начинающуюся в нуле и совпадающую с осью частот (см. табл. 2.6), а мнимая частотная характеристика V(ω)=Kω– есть прямая, проходящая через начало координат с коэффициентом наклона К (см. табл.2.6).

Выражение для АЧХ имеет вид

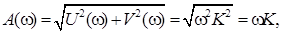
что соответствует прямой, проходящей через начало координат с коэффициентом наклона К (см. табл. 2.6). Возрастающий характер АЧХ этого звена указывает на то, что с увеличением частоты входного сигнала увеличивается амплитуда выходного сигнала. Это означает, что дифференцирующее звено хорошо пропускает сигнал высокой частоты и подавляет низкочастотные сигналы.

Таблица 2.6

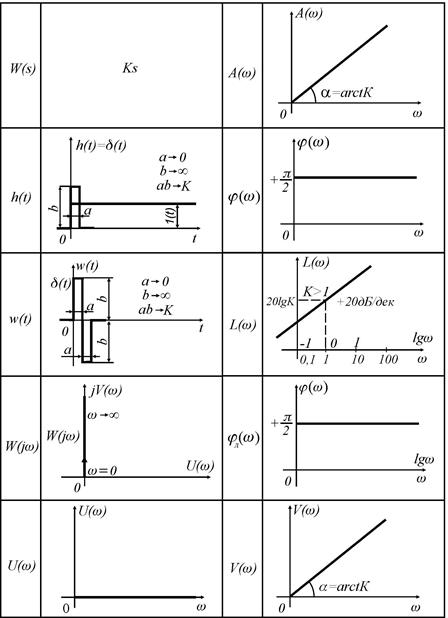
Динамические характеристики идеального дифференцирующего звена

ФЧХ идеального дифференцирующего звена

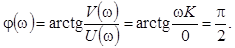
Это прямая, параллельная оси абсцисс, проходящая на уровне 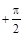(см. табл. 2.6), что соответствует постоянному опережающему сдвигу по фазе выходного сигнала относительно входного.

ЛАЧХ имеет следующее выражение:

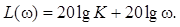
Здесь первое слагаемое – постоянная величина, а второе слагаемое представляет пропорциональную зависимость. Следовательно, ЛАЧХ представляет прямую, проходящую через точку с координатами [20lgК;ω=1]. Наклон прямой определим так: при изменении частоты на декаду происходит изменение амплитуды на величину

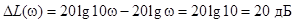Это означает, что ЛАЧХ имеет наклон +20 дБ/дек (табл. 2.6). ЛФЧХ представляет ФЧХ, построенную в логарифмическом масштабе частот. Это прямая, параллельная оси lgω и отстоящая от нее на 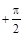(см. табл.2.6).

Примером идеального дифференцирующего звена может служить тахогенератор постоянного тока, если входной величиной является угол поворота вала якоря, а выходной – напряжение, снимаемое со щеток якоря.

Апериодическое, или инерционное, звено и его динамические характеристики

Апериодическим звеном называется звено, уравнение движения которого представляет собой дифференциальное уравнение 1-го порядка

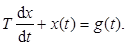
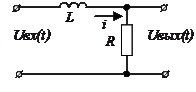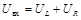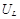Такое звено должно содержать элемент, способный запасать энергию, и элемент, создающий сопротивление потоку энергии, на котором эта энергия рассеивается. Подобными свойствами в электрическом контуре обладают индуктивность или емкость и сопротивление. Определим дифференциальное уравнение цепи RL (рис. 2.15). По закону Кирхгофа можно написать , где и 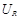— соответственно падение напряжения на индуктивности L и активном сопротивлении R:

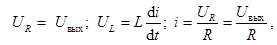
тогда

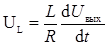Подставим полученные значения в уравнение Кирхгофа

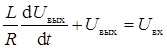где 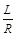=Т — постоянная времени звена.

Обозначив U_вх(t)=g(t), U_вых(t)=x(t), получим дифференциальное уравнение апериодического звена в общем виде

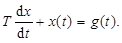
Используя преобразование Лапласа, найдем передаточную функцию звена

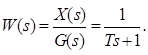
Данная зависимость совпадает с выражением, полученным для инерционного звена при разбиении системы на элементарные звенья с условием, что К=1. В общем случае коэффициент усиления отличен от 1, поэтому передаточная функция инерционного звена записывается в виде

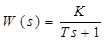. (2.63)

Переходная функция h(t)звена может быть получена в результате решения уравнения движения звена при единичном входном сигнале и нулевых начальных условиях одним из изложенных методов. Воспользуемся методом преобразования Лапласа с применением теоремы разложения Хевисайда:

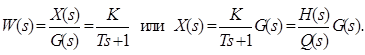
При g(t)=1(t), получим, 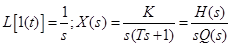. Согласно теореме разложения переходная функция h(t)находится как обратное преобразование Лапласа для Х(s),определяемое из соотношения

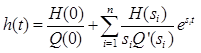, (2.64)

где s_i – корни уравнения Q(s)=0,а n — число корней.

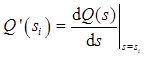Запишем значения всех величин, входящих в (2.64):

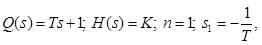
так как Ts+1=0, а s₁=-1/T.

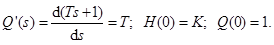
Подставляя эти значения в (2.64), получим

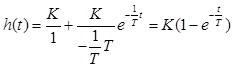Это уравнение экспоненты (табл. 2.4). Физически такой вид переходного процесса определяется наличием в инерционном звене тормозящих факторов в виде сил, моментов, напряжения и других величин, пропорциональных скорости изменения выходной величины.

Весовая характеристика w(t). Продифференцируем выражение для переходной функции по времени

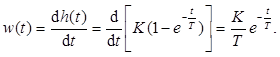
Такой вид (см. табл. 2.4) имеет реакция инерционного звена на воздействие в виде δ-функции.

КЧХ инерционного звена

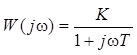Для ее построения необходимо выделить вещественную и мнимую частотные характеристики

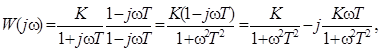
Откуда .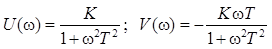

Изменяя значение частоты ω от 0 до ∞, получим кривые для U(ω), V(ω)и W(jω). При ω=0: U(ω)=K ; V(ω)=0, при ω=1/T: U(ω)=K/2; V(ω)=-K/2; при ω→∞: U(ω)→0, V(ω)→0.

Таким образом, ВЧХ – U(ω) представляется убывающей функцией с возрастанием ω (см. табл. 2.4); МЧХ – V(ω) — отрицательная функция, возрастающая по модулю в области частот от 0 до ω_c=1/T и убывающая по модулю при увеличении частоты выше, чем 1/T (см. табл. 2.4); КЧХ – это полуокружность радиусом K/2, расположенная в 4-й четверти (см. табл. 2.4).

АЧХ можно получить из частотных характеристик U(ω)и V(ω)

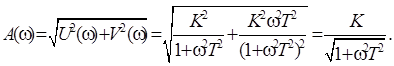
Изменяя ω от 0 до ∞, получим кривую А(ω) (см. табл. 2.4).

ФЧХ инерционного звена ,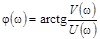

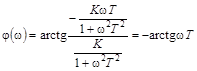При ω=0, φ(ω)=0; ω=1/T,φ(ω)=-45°; ω→∞, φ(ω)→-90°. Следовательно, с изменением частоты ω от 0 до ∞ сдвиг по фазе между входным и выходным сигналами в инерционном звене меняется от 0 до 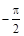(см. табл. 2.4).

ЛАЧХ инерционного звена. Прологарифмируем уравнение АЧХ инерционного звена:

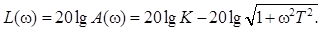
При ω=0 второе слагаемое равно нулю и L(ω)=20lgK. При К>1 L(ω)=20lgK соответствует некоторой положительной ординате. С увеличением ω второй член будет возрастать. Однако в полосе частот от 0 до 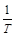влияние второго члена незначительно, поэтому можно считать, что в этой полосе частот L(ω) сохраняет свое постоянное значение, равное L(ω)=20lgK, т.е. характеристика представляет прямую, параллельную оси lgω, приподнятую относительно этой оси на величину 20lgK. При 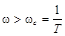влияние второго члена становится существенным и L(ω)уменьшается. При дальнейшем увеличении ω значением 1 по сравнению с величиной ω²T² в выражении 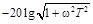можно пренебречь, тогда получим

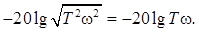
Таблица 2.4

Динамические характеристики апериодического (инерционного) звена

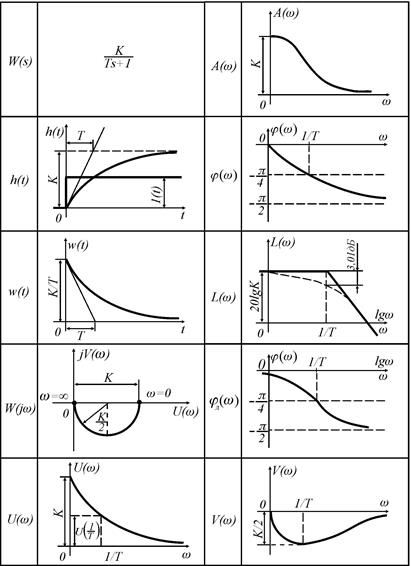
Отсюда видно, что изменение L(ω) при ω>ω_c происходит по пропорциональному закону, следовательно, ЛАЧХ в этом диапазоне частот будет представлять прямую линию с определенным наклоном. Определим наклон этой прямой. При изменении частоты на одну декаду, т. е. при ее десятикратном увеличении получим

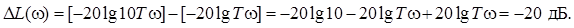
Это значит, что ЛАЧХ инерционного звена представляет две сопрягающиеся прямые: одна параллельна оси абсцисс, а вторая начинается с точки с координатами [20lgK; ω=ω_c] и имеет наклон -20 дБ/дек (см. табл. 2.4).

Частота 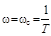, соответствующая точке сопряжения двух прямых, называется частотой сопряжения. Представление ЛАЧХ в виде прямых является приближенным, однако погрешность в результате такого приближения невелика. Точное изображение L(ω) показано штриховой линией (см. табл. 2.4). Из сравнения видно, что наибольшая ошибка, получаемая в результате приближения, возникает при частоте сопряжения 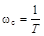. Определим величину этой ошибки:

дБ.

Ошибка равна 3 дБ.

ЛФЧХ – это характеристика 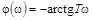в логарифмическом масштабе частот. Следовательно, при изменении ω от 0 до ∞ -φ(ω) изменится от 0 до 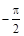. Однако кривая в логарифмическом масштабе будет отличаться от кривой ФЧХ. Она напоминает вид развернутой тангенсоиды. Точка перегиба ЛФЧХ находится на уровне абсциссы, соответствующей частоте сопряжения (см. табл. 2.4).

Дата добавления: 2022-06-11; просмотров: 46; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!